本記事は教養記事シリーズその29です。その他の教養記事はコチラの目次をご覧ください。
RSAとは?
どのような仕組み?
使われている数学理論は?
何がポイント?
RSAとは
RSAとは公開鍵暗号化方式を実現するための手法の1つです。RSAという名前は,開発メンバーであるリベスト氏,シャミア氏,エーデルマン氏の頭文字に由来しています。公開鍵暗号化方式に関しては,コチラの記事で丁寧に解説しています。RSA以外にも,暗号化方式ではいろいろな手法(アルゴリズム)が用いられてきました。
【共通鍵暗号化方式の手法】
●DES:安全性が低い
●トリプルDES:ある程度安全だが計算量が多い
●AES:最も広く利用されている
【公開鍵暗号化方式の手法】
●DH:ある程度安全だが計算量が多い
●ECC:処理速度早いが安全性と利便性△
●RSA:最も広く利用されている
RSAの流れ
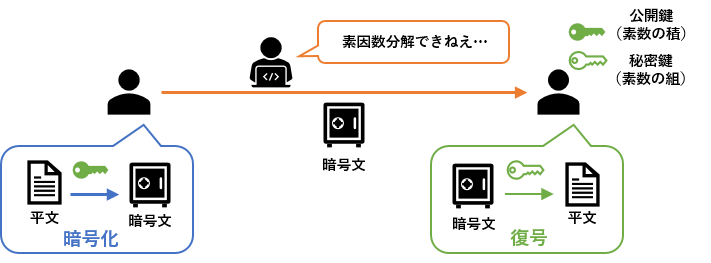 RSAの流れ
RSAの流れRSAの詳しい解説に入る前に,全体の流れを説明しておこうと思います。RSAでは「大きな数の素因数分解がとても難しい」という性質を利用して暗号化を行います。コチラの記事で例えているように,レシピ通りにカレーを作ることは簡単でも,出されたカレーから具材の種類と量を完璧に言い当てることは難しいです。それと同じで,大きな数を素因数分解するのは非常に難しいのです。
 カレーの具材を正確に言い当てられない
カレーの具材を正確に言い当てられないそして,素因数分解することで得られる情報は数学の定理に応用されます。「オイラーの定理」と呼ばれる有名な定理を利用することで,RSA暗号化のしくみは成り立っています。
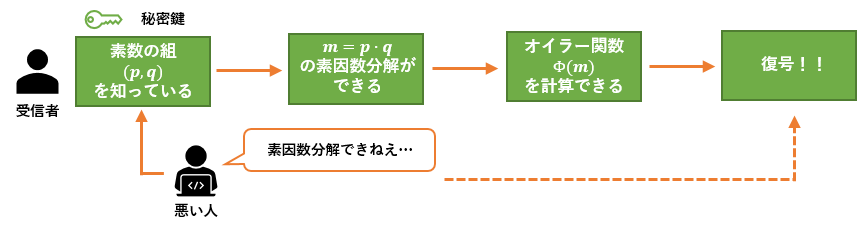 得られた情報は数学の定理を利用します
得られた情報は数学の定理を利用します利用する数学の定理
さて,ここから数式を利用していきます。身構える必要はありません!一緒に少しずつ着実に理解していけば大丈夫です。RSAでは,主に「オイラーの定理(→フェルマーの小定理)」「ユークリッドの互除法」「一次不定方程式の整数解の存在定理」が用いられます。順番に確認していきましょう。
【オイラーの定理】
正の整数$a$,$m$に対して,$a$, $m$が互いに素であるとき,以下が成り立つ。
\begin{eqnarray}
a^{\varphi(m)}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
ただし,$\varphi(m)$は「$m$より小さい正の整数のうち,$m$と互いに素な数の個数」を表すオイラー関数とする。
【フェルマーの小定理】
オイラーの定理において,正の整数$m$が素数$p$であるとき,以下が成り立つ。
\begin{eqnarray}
a^{(p-1)}\equiv1\ ({\rm mod}\ p)
\end{eqnarray}
【ユークリッドの互除法】
自然数$a$,$b(a≥b)$に対して,$a$を$b$で割った余りを$r$とおくとき,以下が成り立つ。
\begin{eqnarray}
gcd(a, b)=gcd(b, r)
\end{eqnarray}
ただし,$gcd(a, b)$は$a$と$b$の最大公約数を表す。
【一次不定方程式の整数解の存在定理】
$a$,$b$を互いに素な整数としたとき,以下の方程式を満たすような整数解$u$,$v$が存在する。
\begin{eqnarray}
au+bv=1
\end{eqnarray}
これらの定理を利用して,RSAのしくみを探っていきたいと思います。
数学的な説明
ここからは,文字を利用して数学的な解説をしていこうと思います。数学が苦手な方も,1行ずつ追いつくようにすれば必ず理解できると思いますので,一緒に頑張っていきましょう。
まずは,文字を決めます。
$A$:平文
$B$:暗号文
$p$:大きな素数
$q$:大きな素数
$l_a$:復号のための定数$(>0)$
$l_b$:暗号化のための定数
$m$:公開鍵の要素
$k$:公開鍵
$s$:秘密鍵
ただし,以下のように定めます。
$m=p \cdot q$
$k=\{l_b, m\}$
$s=l_a$
このとき,平文と暗号文は以下のように表されます。
\begin{eqnarray}
B \equiv A^{l_b}\ ({\rm mod}\ m)\\
A \equiv B^{l_a}\ ({\rm mod}\ m)
\end{eqnarray}
その通りです。少し,今の状況を整理します。
$A$:平文→知っている
$B$:暗号文→方法は知っている
$p$:大きな素数→適当に作る
$q$:大きな素数→適当に作る
$l_b$:暗号化のための定数→知らない
$l_a$:復号のための定数→知らない
$m$:公開鍵の要素→知っている
$k$:公開鍵→片方知らない
$s$:秘密鍵→知らない
ただし,以下のように定めます。
$m=p \cdot q$
$k=\{l_b, m\}$
$s=l_a$
というような具合です。そこで,以下では「知らない」となっている要素に関して,数学の定理を利用しながら求めていきたいと思います。まずは,式(5)に式(6)を代入します。そうすると,このようになります。
\begin{eqnarray}
B \equiv B^{l_{a}l_{b}}\ ({\rm mod}\ m)
\end{eqnarray}
今後,この式(7)が成立することを証明すれば,暗号化と復号が上手くいっている証明になります。そこで,式変形を進めていきたいと思います。両辺を$B$で割ると
\begin{eqnarray}
B^{l_{a}l_{b} – 1}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
その通りです。オイラーの定理と少し並べてみてみましょう。
【オイラーの定理】
\begin{eqnarray}
a^{\varphi(m)}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
【今回の式】
\begin{eqnarray}
B^{l_{a}l_{b} – 1}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
オイラーの定理の要件は,$a$,$m$が正で互いに素であることでしたから,$B$が正,かつ$B$と$m$が互いに素であるという条件下で「$\varphi(m)=l_{a}l_{b} – 1$」となる$l_a$と$l_b$を作ることができるということを示せば,式(7)が成立していることを示すことができます。
さて,「$\varphi(m)=l_{a}l_{b} – 1$」を式変形してみましょう。
\begin{eqnarray}
l_{a}l_{b} – \varphi(m) = 1
\end{eqnarray}
その通りです。しかし,$\varphi(m)$に係数がかかっていないので定理を適用することができません。そこで,式(10)をいじってから式を変形していくことにします。$w (≠0)$を利用して,式(10)の両辺を$\frac{1}{w}$乗してみます。
\begin{eqnarray}
B^{\frac{l_{a}l_{b} – 1}{w}}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
この状態で,先ほどと同じような操作をすると,以下の等式が得られます。分かりやすいように,$-w$を$v$とおくことにします
\begin{eqnarray}
l_{a}l_{b} – \varphi(m)w = 1
\end{eqnarray}
\begin{eqnarray}
l_{a}l_{b} + \varphi(m)v = 1
\end{eqnarray}
見事,式(4)の形と一致しました。ここで,1つ問題があります。式(4)と見比べる時に,$l_a$と$l_b$のどちらを$u$とみなすかという問題です。これは,$l_a$と$l_b$の意味をよく考えれば分かります。公開するのは$l_b$の方です。ですので,式(14)の要件を満たす形で$l_b$を決めてから,式(14)に当てはめて$l_a$を求めて復号のための秘密鍵$s$とすればよいのです。
式(14)の要件というのは「$l_b$と$\varphi(m)$が互いに素」という条件でしたから,そのように$l_b$を定めればよいということになります。ちなみに,$l_a$に関しては「$l_a>0$」という要件が残っています。これに関して証明を加えておきます。つまり,式(14)を満たす$l_a(>0)$が存在することを示します。
式(14)を満たす整数$l_a$と$v$は定理より見つかりますから,適当に見つけたとします。それらを$l_{a_0}$,$v_0$と置きます。このとき,以下が成り立ちます。
\begin{eqnarray}
l_{b}l_{a_0} + \varphi(m)v_0 = 1
\end{eqnarray}
式(15)を整数nを利用して少しいじると
l_{b}(l_{a_0} + \varphi(m)n) + \varphi(m)(v_0 – l_{b}n) = 1
\end{eqnarray}
$A$:$B^{l_a}\ ({\rm mod}\ m)$
$B$:$A^{l_b}\ ({\rm mod}\ m)$
$p$:大きな素数→適当に作る
$q$:大きな素数→適当に作る
$l_b$:暗号化のための定数→$\varphi(m)$と互いに素
$l_a$:復号のための定数→式(14)を満たす形で決定
$m$:公開鍵の要素→$p$と$q$から計算
$k$:公開鍵→決まる
$s$:秘密鍵→$l_a$と同じ
心配いりません。$\varphi(m)$は$m=pq$より小さい正の整数のうち,$m=pq$と互いに素な数の個数を表しているのでした。$p$と$q$は素数ですので,$m$より小さな$m-1$個の正数から,$p$の倍数と$q$の倍数の数を引けばよいです。
$m$よりも小さな$p$の倍数は,$p,2p,\ldots,(q-1)p$の$q-1$個です。同様に,$m$よりも小さな$q$の倍数は,$q,2q,\ldots,(p-1)p$の$p-1$個です。以上から,$\varphi(m)$を計算することができます。
\begin{align}
\varphi(m) &= (pq-1)-(q-1)-(p-1) \\
&= pq-p-q+1 \\
&= (p-1)(q-1)
\end{align}
ちなみに,RSA暗号の説明の中には,$p-1$と$q-1$の最小公倍数を用意するものもあります。これは,$\varphi(m)$と互いに素な整数$l_b$を探すという$\varphi(m)$本来の役割に着目したものです。$l_b$を探す場面に限定すれば,$p-1$と$q-1$の最小公倍数$L$を考えれば十分だからです。
\begin{eqnarray}
L = \rm{lcm}[p-1, q-1]
\end{eqnarray}
ただし,$\rm{lcm}[\alpha, \beta]$は$\alpha$と$\beta$の最小公倍数を表します。このとき,整数$k$を用いて$\varphi(m)$は以下のように表されます。
\begin{align}
\varphi(m) &= kL
\end{align}
式(14)に代入すると,以下が得られます。
\begin{align}
l_{a}l_{b} + kLv &= 1 \\
l_a l_b + Lv &= 1
\end{align}
ただし,$kv$を改めて$v$と置き直しました。以上の議論から,RSAの定式化において$\varphi(m)$の代わりに$L$を考えても破綻しないことが分かりました。逆に言えば,わざわざ最小公倍数を持ち込まなくてもRSAの定式化は可能ですが,一般に$p-1$と$q-1$の積を取ると桁数が大きくなってしまうため,計算を簡単にするという観点から$\varphi(m)$ではなく$L$が好んで利用されるようです。
いい指摘です。$l_a$の存在は示せましたが,それを実際に計算で求めることは可能なのかという疑問ですね。これについては,「係数が互いに素である一次不定方程式はユークリッド互除法を利用して解を求めることができる」という定理があります。そちらを利用すれば,ユークリッドの互除法を計算方法として利用して$l_a$を求めることができることが分かりました。
具体的には,式(14)「$l_{a}l_{b} + Lv = 1$」を満たす$l_a$を求めればよいのですが,$v$は途中で途中で勝手に定めた定数ですので,modを利用してvを無くします。すなわち,
\begin{eqnarray}
l_{a}l_{b} \equiv 1\ \rm{mod}\ L
\end{eqnarray}
を満たす形で$l_a$を決定すればよいことになります。これにて,RSA暗号化方式の証明が完了しました。
RSAの流れ再確認
 RSAの流れ
RSAの流れ1.定数の設定
$p$:大きな素数を適当に作る
$q$:大きな素数を適当に作る
$m$:公開鍵の要素→$p$と$q$から計算
$L$:$\rm{lcm}[p-1, q-1]$として定める
$l_b$:$L$と互いに素となるように作る
$l_a$:「$l_{a}l_{b} \equiv 1\ \rm{mod}\ L$」を満たす形で決定
$k$:$l_b$と$m$によって定まる
$s$:$l_a$と同じ
2.暗号化と復号
$A$:$B^{l_a}\ ({\rm mod}\ m)$
$B$:$A^{l_b}\ ({\rm mod}\ m)$
実際に,簡単な素数を用いて公開鍵を暗号鍵を生成してみましょう。まず,自分で定めるのは$p$と$q$でした。ここでは,簡単に$p=17, q=19$としましょう。続いて,公開鍵の要素である$m$を求めます。$p$と$q$の積ですので,$323$と求められます。
続いて,$p-1$と$q-1$の最小公倍数である$L$を求めましょう。$L=\rm{lcm}[16, 18]=144$となります。
次に求めるのは,$l_b$です。$l_b$は$L$と互いに素であればOKですから,その中で一番小さな値を設定しましょう。つまり,$l_b=5$です。$l_b$が求まりましたので,$l_a$も求めることができます。$l_{a}l_{b} \equiv 1\ (\rm{mod}\ L)$を満たすように$l_a$を設定しましょう。
$l_b$と$L$を代入すれば,$l_{a}\cdot 5 \equiv 1\ (\rm{mod}\ 144)$となります。これを満たす$l_a$は,最も簡単な候補としては$144/5 + 1 \fallingdotseq 29$ となります。実際に,$l_a = 29$を$l_{a}\cdot 5 \equiv 1\ (\rm{mod}\ 144)$に代入してみると,$29 \cdot 5 = 145 \equiv 1\ (\rm{mod}\ 144)$となり,確かに成立していることが分かります。以上で,公開鍵と秘密鍵の生成は完了しました。
【生成された鍵ペア】
●公開鍵:$l_b = 5, m=323$
●秘密鍵:$l_a = 29$
実際に確認してみる
以上の設定を用いて,平文$A=10$を暗号化し,復号してみましょう。暗号化の式から,
\begin{eqnarray}
B=10^{5}\;({\mathrm mod}\;323)=193
\end{eqnarray}
となります。また,復号化の式に従って計算を行うと,
\begin{eqnarray}
193^{29}\;({\mathrm mod}\;323)=10
\end{eqnarray}
となり,元の平文$10$が復号されることが確認できました.
ひとこと
非常にややこしい分野でした。多くの人が,「RSAは桁数の大きい素因数分解が大変であること」を利用していることは知っているかと思います。しかし,ここまで踏み込んで理解している人はごく少数だと思われます。個人的に美しいのが,暗号化にまでも「オイラーの定理」が応用されていることです。「数学が役に立つ例」として非常に分かりやすいのは今回のRSAではないでしょうか。

















コメント失礼します。大変わかり易い解説ありがとうございます。1点だけ、なぜφ(m)がmより小さい正の整数の積の最大公約数となるのか、何度読み返しても理解できませんでした。可能であれば補足説明して頂けないでしょうかm(_ _)m
tanaka様
ご連絡ありがとうございます。
本記事はかなり前に執筆した文章でして,誤植が多く大変失礼いたしました。
自分の理解が間違えていたため,本文を修正しました。
他にも,modがローマン体になっていないなど,数式として不適切な表記も混在していますが,何卒ご容赦ください。
早速のご回答と訂正ありがとうございます。腹落ちさせる事ができ、スッキリしました。大変勉強になりました。ありがとうございました。
度々申し訳ありません。φ(m)をp-1とq-1の最小公倍数に置き換える事ができる理由について、補足説明して頂く事は出来ませんでしょうか?お時間ある時で結構ですので、どうか宜しくお願い致します。
tanaka様
ご質問ありがとうございます。
本文を加筆してみました!書き殴りで恐縮ですが,これで疑問は解決できそうでしょうか??
ありがとうございます!色んなサイトを見ましたが、最小公倍数を使う理由がイマイチ説明されておらず、質問させて頂きました。(p-1)(q-1)より、lcm[p-1,q-1]の方が、lbを探す手間が省けると言う理解で合ってますでしょうか??
丁寧な補足のご説明、ありがとうございました。疑問が解消され、腹落ちさせることができました。本当にありがとうございましたm(_ _)m
tanaka様
ご返信が遅れてしまい大変申し訳ありません!
正確なことは言えないのですが,恐らくオーバーフロー対策として最小公倍数を用いるものと思われます。
以下のopensshの実装を覗いてみると,どのようにrsaが実装されているのかが理解でき,計算量やオーバーフロー等の観点も理解しやすいかと思われます。
https://github.com/openssh/openssh-portable/blob/master/ssh-keygen.c
こちらでは確認する時間が取れず恐縮ですが,参考にしていただければと思います。