【世界一分かりやすい解説】イラストでみるTransformer

本記事はThe Illustrated Transformerを和訳した内容になります。引用元はJay Alammarさん（@JayAlammar）が執筆されたブログ記事で，MITの授業でも実際に利用されています。

はじめに

前回の記事では，注意機構についてお伝えしました。注意機構とは，現代の深層学習において至る所で利用されている手法で，ニューラル機械翻訳の精度向上に大きく貢献した概念です。本記事では，注意機構を利用してモデルの学習速度を向上させるTransformerについて見ていきましょう。Transformerは特定のタスクにおいて，Googleのニューラル機械翻訳を上回る性能を発揮します。しかし，最大の利点は，Transformerが並列計算に適した手法だということです。実際に，Google Cloudが提供するCloud TPUを使用する際に，Transformerを参照することが推奨されています。そこで，モデルを分解してパートごとに見ていきましょう。

TransformerはAttention is All You Needという論文内で提唱されました。TensorFlowによる実装は，Tensor2Tensorパッケージの一部として利用可能です。Harvardの自然言語処理グループは，Pytorchの実装を利用した注釈付きの論文ガイドを作成しています。この記事では，概念を少し単純化して，１つ１つ紹介していきます。上手くいくとそこまで深い知識を必要せずとも理解しやすい内容にしていきます。

抽象度の高い視点

まず，モデルを１つのブラックボックスとして見てみましょう。機械翻訳では，ある言語の文章を受け取り，その翻訳を別の言語で出力します。

「Optimus Prime」を開けてみると，エンコーダ構成要素，デコーダ構成要素，そしてそれらを繋げる要素があることが分かります。

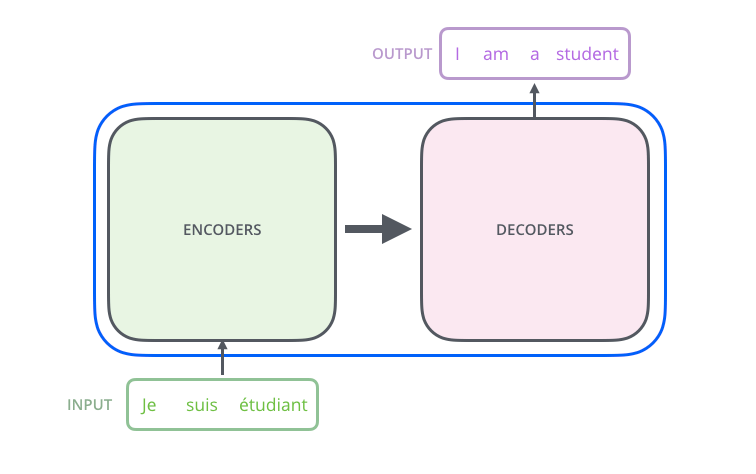
エンコーダ構成要素は，エンコーダの積み重ねからできています（論文中では６つのエンコーダが積み重ねられています。６という数字には特別な意味は込められておらず，他の数字を実験的に試すことができます）。デコーダ構成要素も，デコーダが６つ積み重ねられてできています。

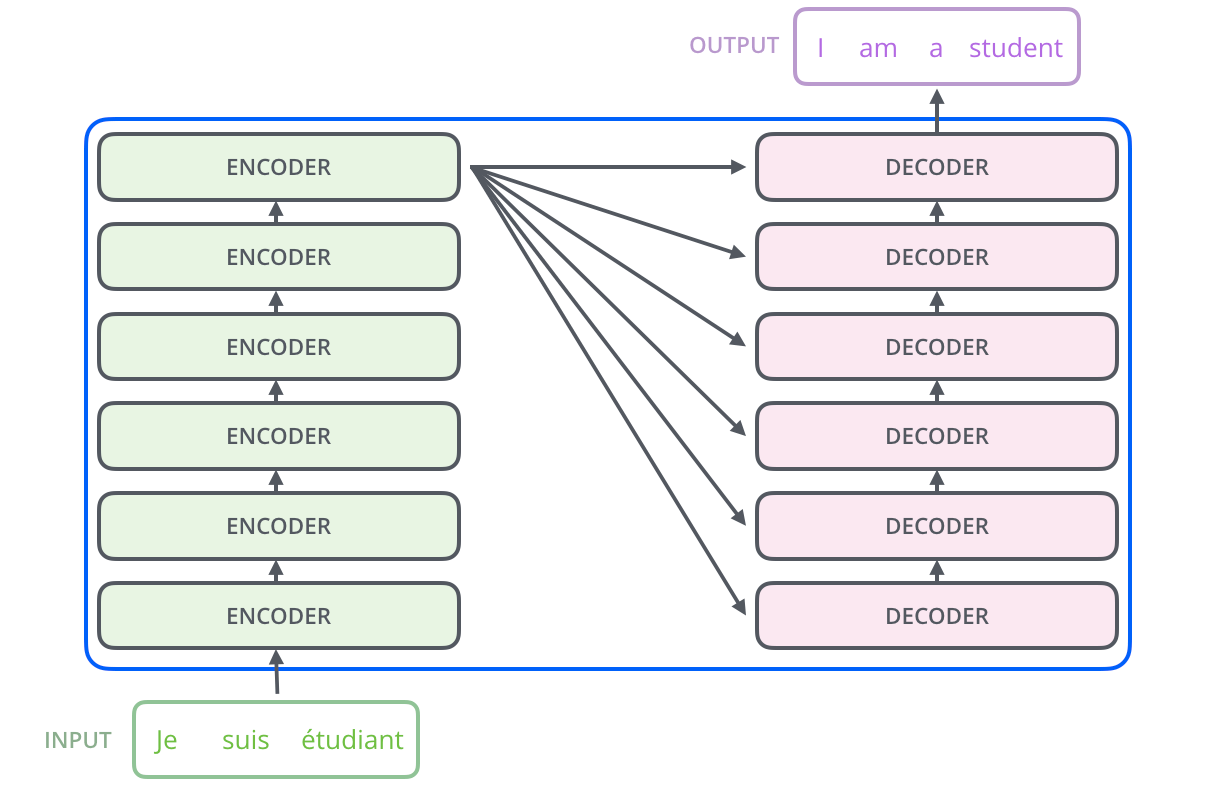
これらのエンコーダは，全て同一の構造をしています（ただし重みは共有していません）。それぞれのエンコーダは，以下のように２つのサブレイヤーに分かれます。

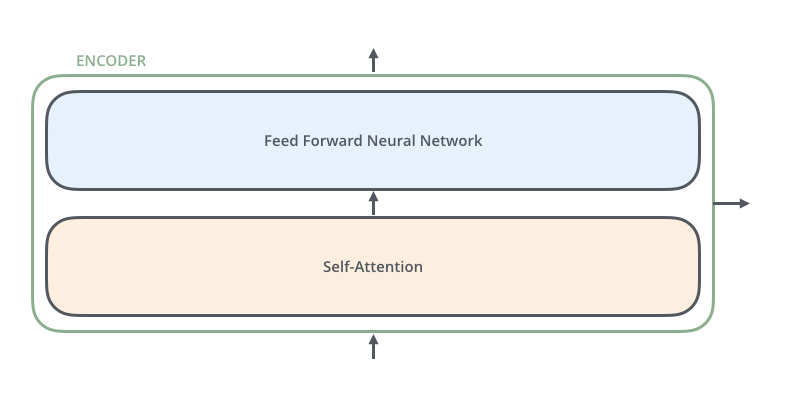
エンコーダの入力は，まず自己注意層を通過します。この自己注意層というのは，エンコーダが特定の単語をエンコードする際に，入力系列中で他の単語を参照するのを助けるものです。

自己注意層の出力は，全結合層に通されます。エンコーダの各位置に全く同じ構造の全結合層が適用されます。

デコーダは自己注意層と全結合層の両方を含みますが，その間には注意機構があり，入力系列のどこに注意するべきかの判断を手助けします（前回の記事でお伝えしているように，seq2seqモデルで注意機構が果たす役割と同じです）。

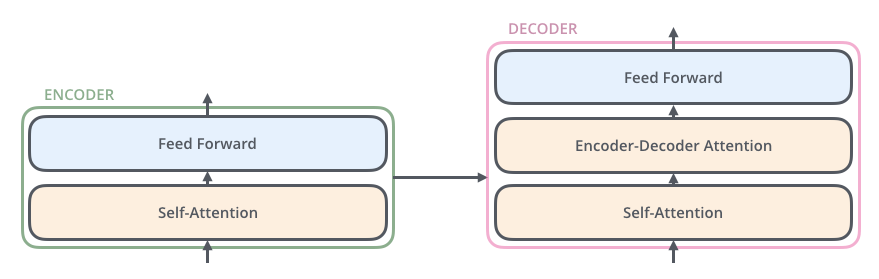
可視化にテンソルを導入

ここまではTransformerの主要な構成要素を見てきましたが，以降は様々なベクトル・テンソルがこれらの構成要素の間でどのように機能して，訓練済みモデルでどのように入力を出力に変換するのかを見ていきましょう。

一般的な自然言語処理の手法と同様に，埋め込みアルゴリズムを利用して各入力単語をベクトルに変換することから始めます。

各単語はサイズが512のベクトルに「埋め込み化」されています。本記事では，これらのベクトルを単純な４つの箱で表現します

単語を埋め込み化する処理は，エンコーダの最下段の前で行われます。全てのエンコーダに共通している抽出処理は，それぞれのサイズが512であるベクトルのリストを受け取るということです。このリストのサイズはハイパーパラメータとして設定できます。基本的には，訓練データセットの中で，最も長い文の長さになります。

単語の埋め込みが終わり次第，それぞれのベクトルはエンコーダを構成する２つのサブレイヤーを通過します。

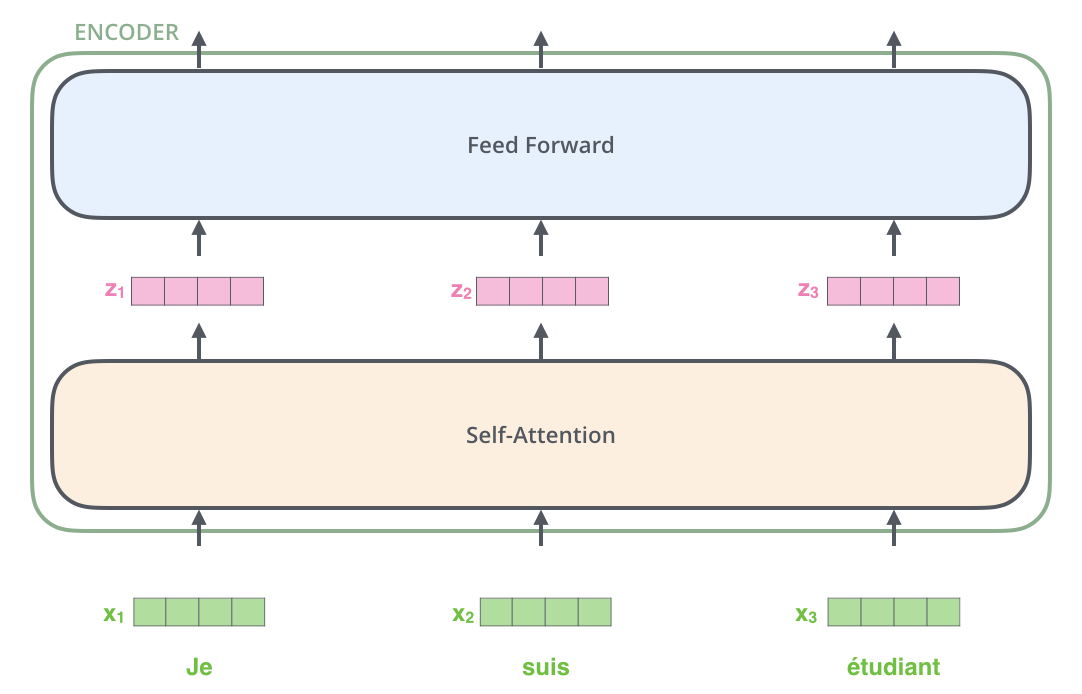
ここで，Transformerの重要な特性の 1 つが見えてきます。それは，各位置にある単語がエンコーダ内のそれ自身のパスを通って流れるということです。自己注意層では，これらのパス間に依存性があります。しかし，全結合層にはそのような依存関係がないので，全結合層を流れる間に様々なパスを並列に実行することができます。

次に，例文を短文に変えて，エンコーダの各サブレイヤーで何が起こっているのかを見ていきます。

さあエンコードの時間です！

すでにお伝えしたように，エンコーダは入力としてベクトルのリストを受け取ります。エンコーダはベクトルのリストを「自己注意」層に渡して処理し，次に全結合層に渡して，次のエンコーダに出力を送ります。

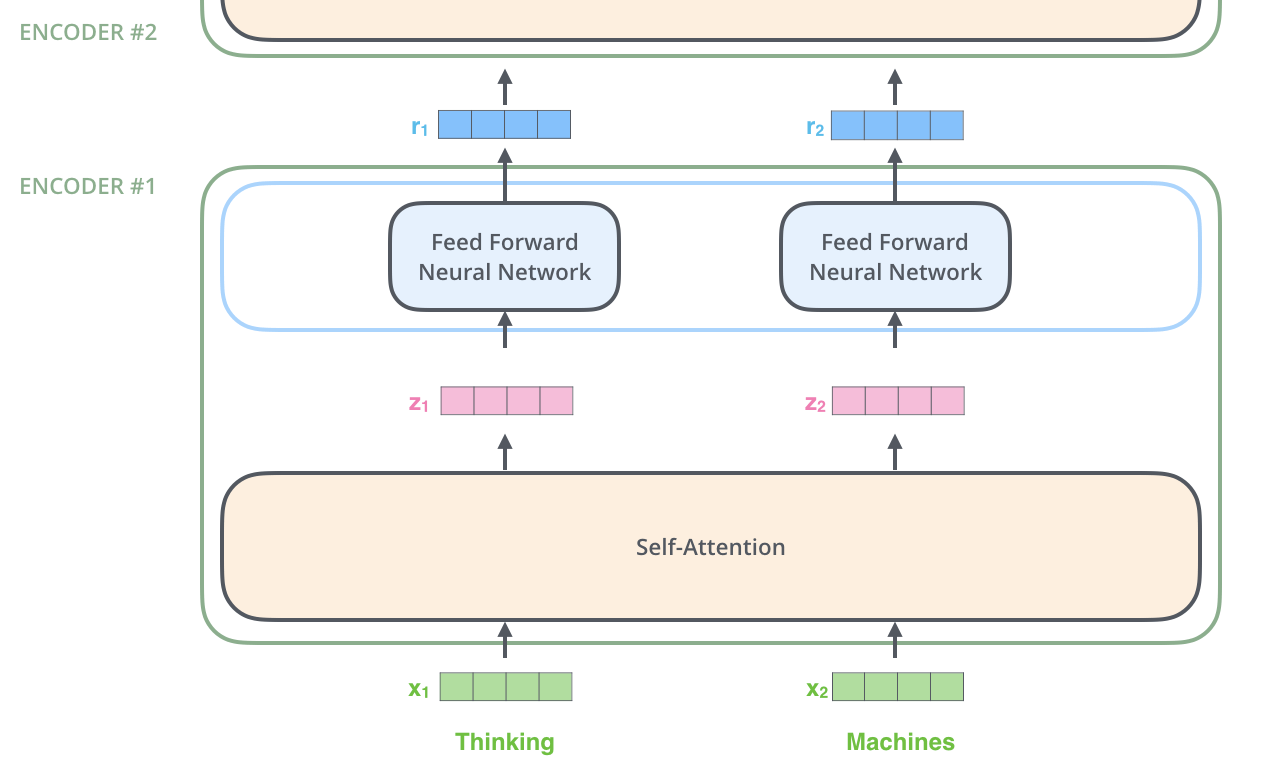
各位置の単語は，自己注意プロセスを通過します。そして，それぞれの単語は全結合層を通過します。

「自己注意」の抽象的な視点

「自己注意」をあたかも誰もがよく知っている言葉として投げかけている私に騙されないでください。実際，私は「Attention is All You Need」を読むまで，この概念に出くわしたことはありませんでした。自己注意がどのように機能しているのかを見ていきましょう。

次の文が翻訳したい入力文だとします。

“The animal didn’t cross the street because it was too tired”

この文章の「it」は何を指しているのでしょうか？「street」のことを指しているのか，それとも動物のことを指しているのか？これは人間にとっては簡単な質問ですが，機械にとってはそう簡単ではありません。

モデルが「it」という単語を処理しているとき，自己注意は「it」を「animal」と関連付けることを可能にします。

モデルが各単語（入力系列の各位置）を処理するときには，自己注意によって単語のより良いエンコーディングにつながる手がかりを得ることができます。すなわち，モデルは入力系列の他の位置を参照することができます。

RNNに詳しい方は，隠れ状態を維持することでRNNは，処理した前の単語（ベクトル）の表現を現在処理している単語に組み込むことができることを思い出してみてください。自己注意は，transformerが他の関連する単語の「理解」を現在処理している単語に組み込むために使用する方法です。

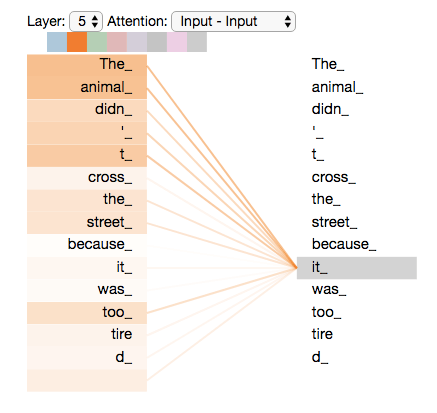
エンコーダ#５（１番上のエンコーダ）では，「it」という言葉をエンコードしています。注意機構の一部は「The animal」に注目していて，その表現の一部を「it」のエンコードに組み込んでいました。

学習済みTransformerモデルを読み込んで，インタラクティブな可視化を通して挙動を調べることができるTensor2Tensor notebookを必ずチェックしてください。

「自己注意」の詳細

まず，ベクトルを使って自己注意を計算する方法を確認してから，行列を使って実際にどのように実装されているのかを見ていきましょう。

自己注意を計算する最初のステップは，エンコーダの各入力ベクトル（ここでは各単語の埋め込み）から3つのベクトルを作成することです。そこで，各単語について，Queryベクトル，Keyベクトル，Valueベクトルを作成します。これらのベクトルは，訓練フェーズで学習した3つの行列に埋め込みを乗算して作成されます。

これらの新しいベクトルは，埋め込みベクトルよりも次元が小さいことに注目してください。埋め込みベクトルとエンコーダの入出力ベクトルの次元は512ですが，新しく作られたベクトルの次元は64です。これは，（ほとんどの場合）多頭注意の計算を一定にするためのアーキテクチャです。

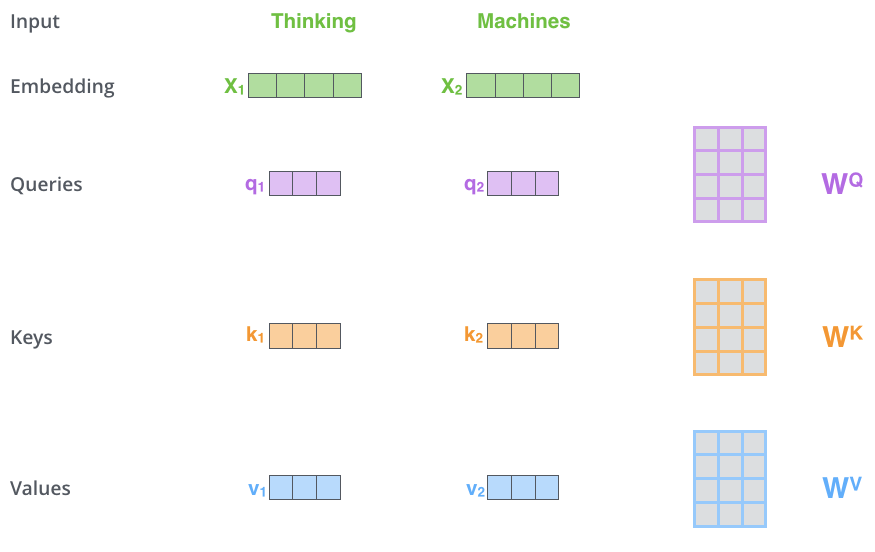
x1にWQ重み行列を乗算すると，その単語に関連付けられた「Query」ベクトルq1が生成されます。このようにして，最終的には入力文の各単語の「Query」ベクトル，「Key」ベクトル，「Value」ベクトルを作成します。

さて，「Query」ベクトル，「Key」ベクトル，「Value」ベクトルとは何なのでしょうか。

これらは，注意を計算したり，注意について考えたりするのに便利な抽象的な概念です。注意がどのように計算されるかを読み進めれば，これらのベクトルが果たすほとんど全ての役割について知ることができます。

自己注意を計算する第二のステップは，スコアを計算することです。今回の例では，最初の単語「Thinking」の自己注意を計算しているとします。この単語に対して，入力文の各単語をスコア化する必要があります。スコアは，ある位置にある単語をエンコードする際に，入力文の他の部分にどのくらいの焦点を当てるかを決定します。

スコアは，Queryベクトルと，注目している単語のKeyベクトルとの内積を取ることで計算されます。つまり，位置1の単語の自己注意を処理している場合，最初のスコアはq1とk1の内積となり，2番目のスコアはq1とk2の内積となります。

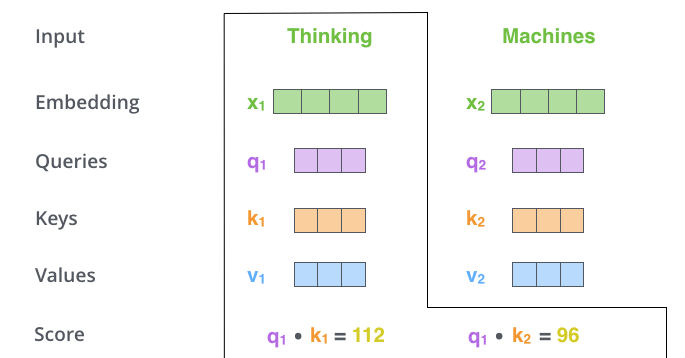
第３および第４のステップは，スコアを８で割ることです（８という数字は論文で使用したKeyベクトルの次元の平方根からきています）。これは，より安定した勾配を保持することにつながります。他の値を指定することもできますが，Keyベクトルの次元の平方根がデフォルトです），そして結果を Softmaxに渡します。Softmaxはすべてを正の値にして，足して１になるようにスコアを正規化します。

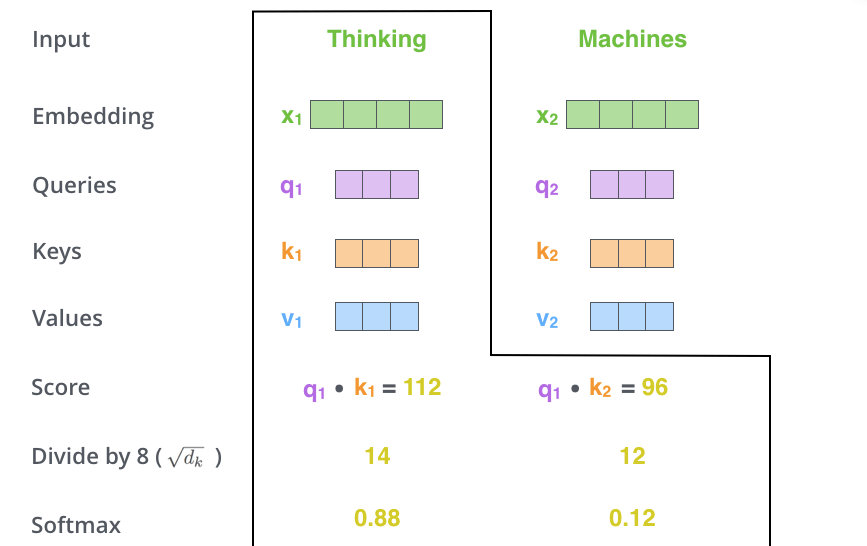
このソフトマックススコアは，各単語がこの位置でどれだけ表現されるかを決定します。明らかに，現在処理している位置にある単語が最も高いSoftmaxスコアを持つことになりますが，時には現在の単語に関連する別の単語に注目することが有用な場合もあります。

5番目のステップは，各ValueベクトルにSoftmaxスコアを掛け合わせます（同時に合計する準備をします）。ここでの直感は，注目したい単語の値をそのままにしておき，無関係な単語を（例えば，0.001のような小さな数字を乗算することで）かき消すことです。

第６のステップは，重み付けされたValueベクトルを足し合わせることである。これにより，現在処理している位置（下の例では最初の単語について）の自己注意層の出力が生成されます。

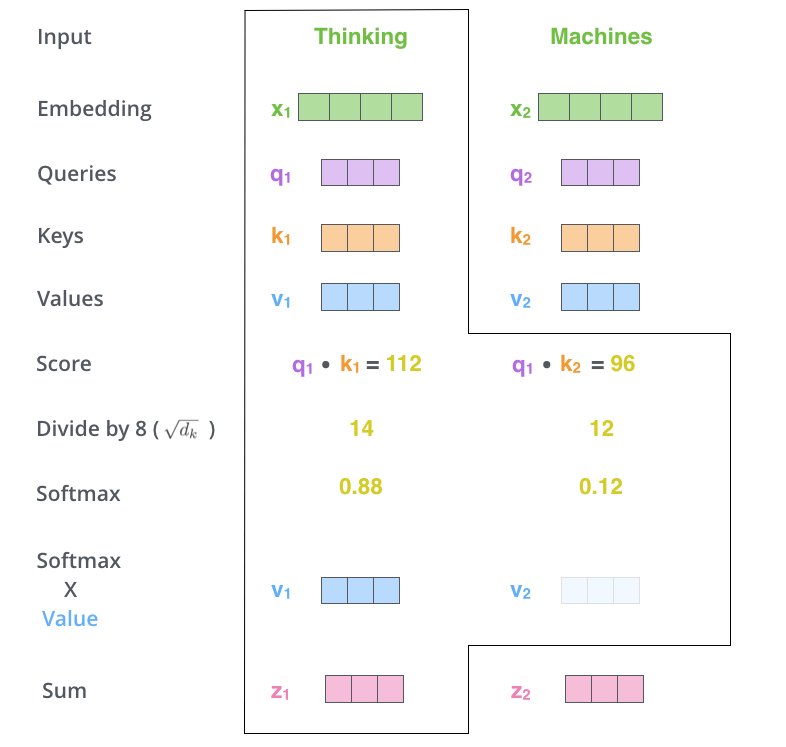
これで自己注意の計算は終了です。結果として得られるベクトルは，全結合層に送られます。しかし，実際の実装ではこれらの計算はより高速な処理のために行列形式で行われます。単語レベルでの直感的な計算方法を見てきましたので，以降は行列形式の計算を見てみましょう。

自己注意の行列形式演算

最初のステップは，Query，Key，Value行列を計算することです。これを行うには，埋め込みベクトルを行列Xに敷き詰め，これに学習した重み行列（WQ, WK, WV）を乗算します。

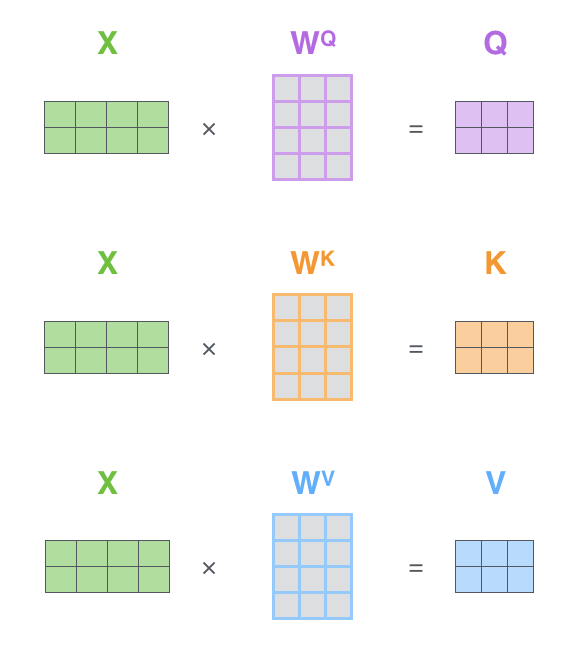
X 行列の各行は，入力文の単語に対応します。埋め込みベクトル（512次元，図では4つのボックス）とq/k/vベクトル（64次元，図では3つのボックス）の大きさの違いを再度確認して下さい。

最後のステップです。今我々は行列を扱っているので，2から6までのステップを1つの式に凝縮して，自己注意層の出力を計算することができます。

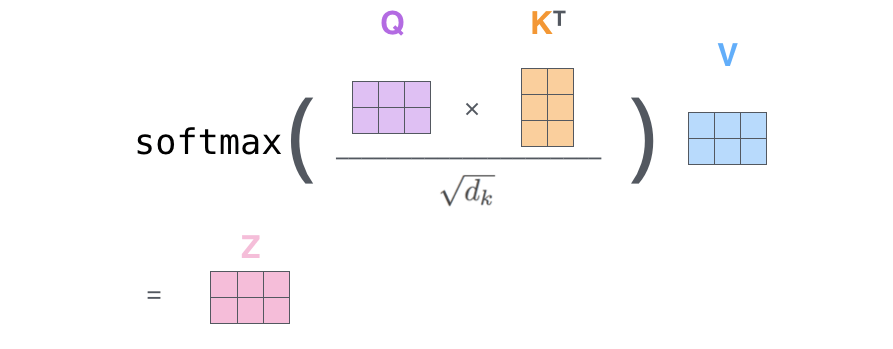
行列形式の自己注意の演算

複数の頭をもつ怪獣

論文では「多頭注意」と呼ばれるメカニズムを追加することで，自己注意層をさらに洗練させました。多頭注意は，以下の2つの方法で注意層の性能を向上させます。

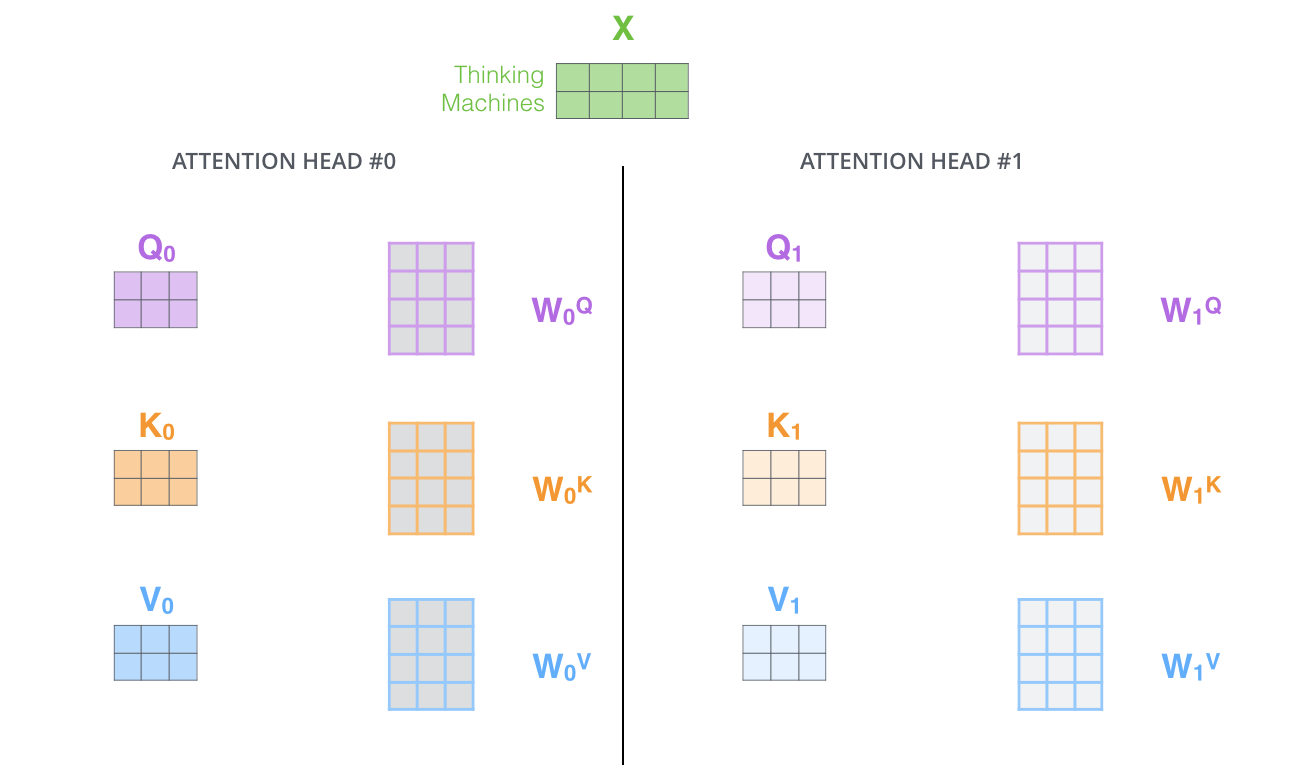
多頭注意では，別々のQuery/Key/Value重み行列を維持し，結果として異なるQuery/Key/Value行列を生成します。以前と同様に，XにWQ/WK/WV行列を乗算してQuery/Key/Value行列を生成します。

上で説明した方法と同じ自己注意の計算を異なる重み行列を用いて8回行うと，8つの異なるZ行列が得られます。

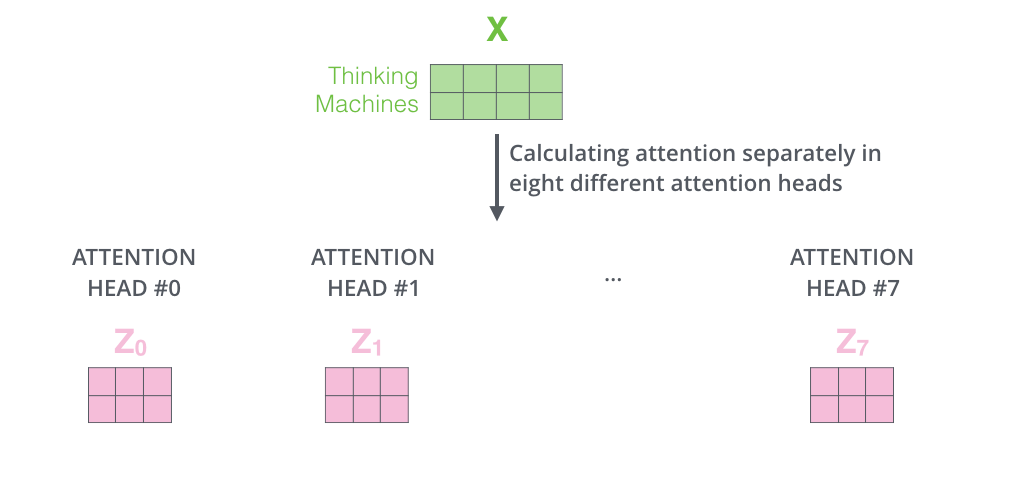
これはちょっとした課題を残しています。全結合層は8つの行列を期待しているのではなく，1つの行列（各単語のベクトル）を期待しています。そこで，この8つの行列を1つの行列に凝縮する方法が必要になります。

どうすればよいのでしょうか？行列を連結してから，重み行列WOを追加してそれらを倍数化すればいいのです。

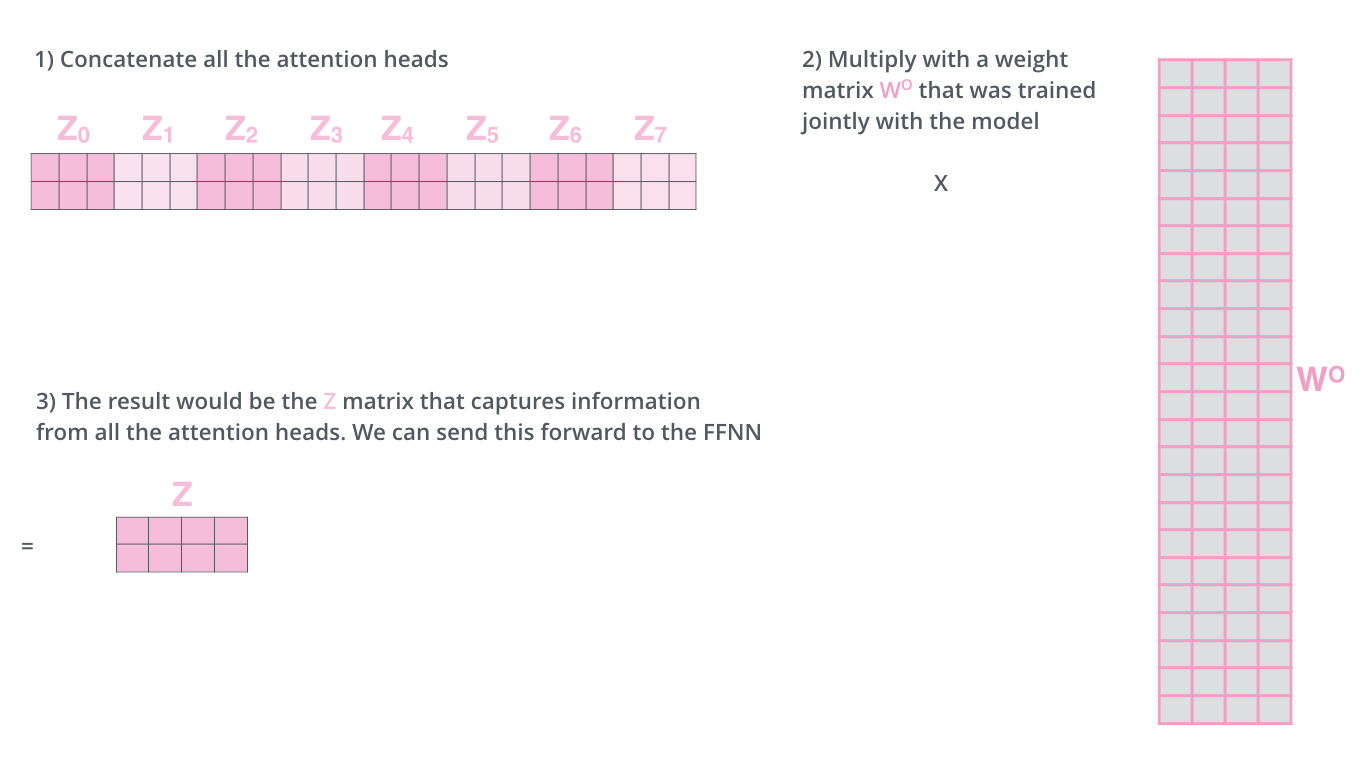
多頭自己注意はこれだけでかなりのものです。多くの行列が出てきましたが，それらを１つのビジュアルにまとめて見られるようにしてみましょう。

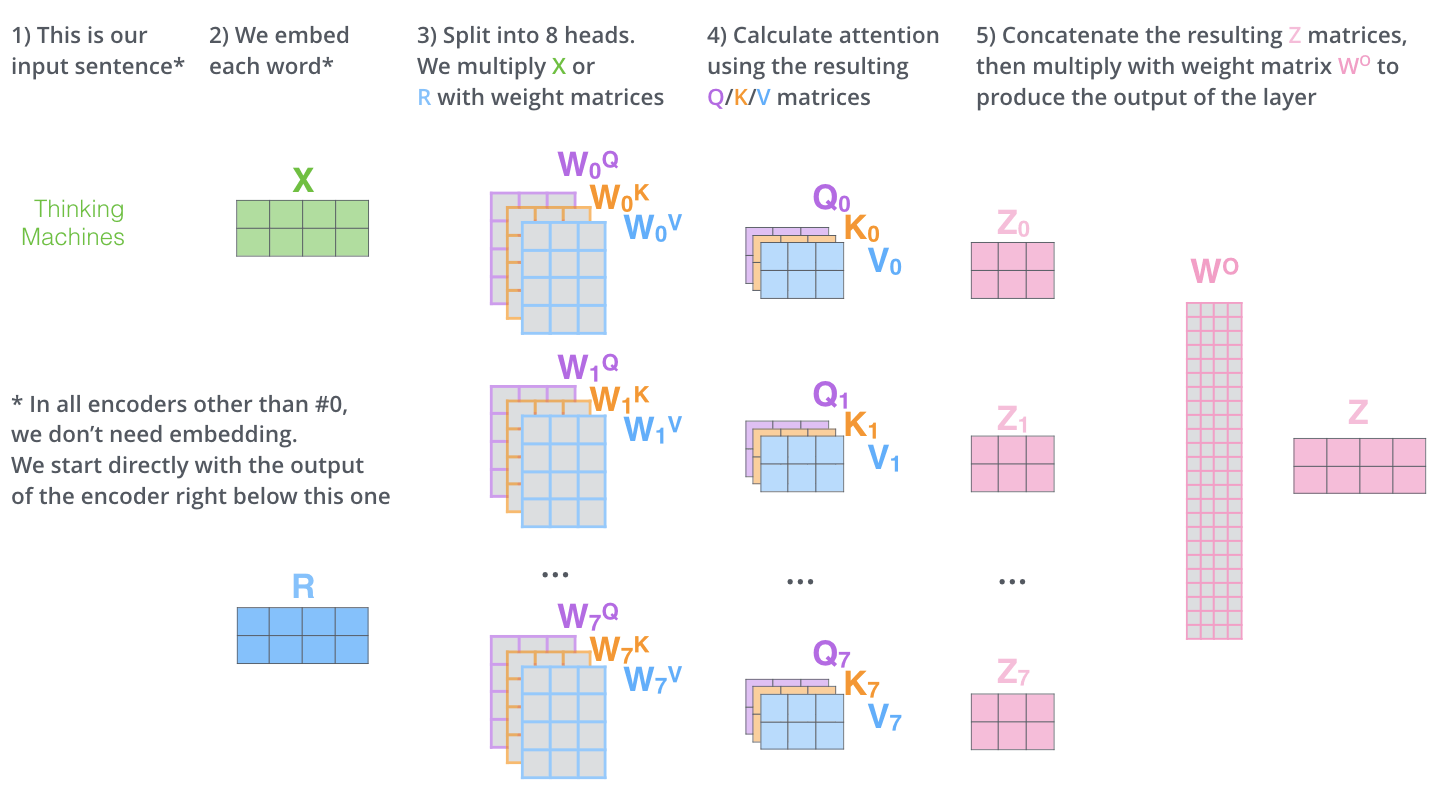
ここでは各自己注意について触れましたが，先ほどの例をもう一度見て例文の中で「it」という単語をエンコードする際に，異なる自己注意がどこに焦点を当てているのかを見てみましょう。

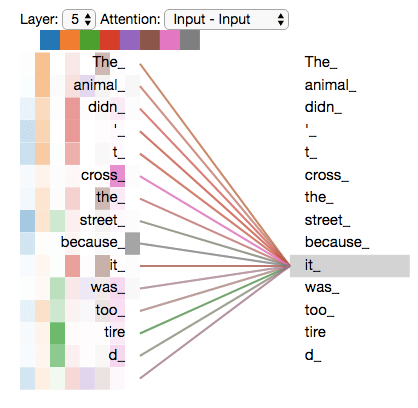
「it」という言葉をエンコードするとき，ある自己注意は「the animal」に最も集中し，別の注目ヘッドは「tired」に集中してることが分かります。ある意味では「it」という言葉のモデルの表現は，「the animal」と「tired」の両方の表現の一部を組み込んでいるといえます。

しかし，すべての自己注意を画像に加えると，解釈するのが難しくなることがあります。

位置符号化を用いた系列順序の表現

上で説明してきたモデルに欠けているものは，入力系列の単語の順序を表現する方法です。

Transformerは各入力にあるベクトル（位置エンコーディングベクトル）を追加します。追加されるベクトルは，モデルが学習する特定のパターンに従い，各単語の位置や系列内の異なる単語間の距離を決定するのに役立ちます。ここでの直感的な理解は，これらの値を埋め込みベクトルに追加することで，埋め込みベクトルがQuery・Key・Valueベクトルに変換された後，内積を取ると埋め込みベクトル間の意味のある距離が得られるということです。

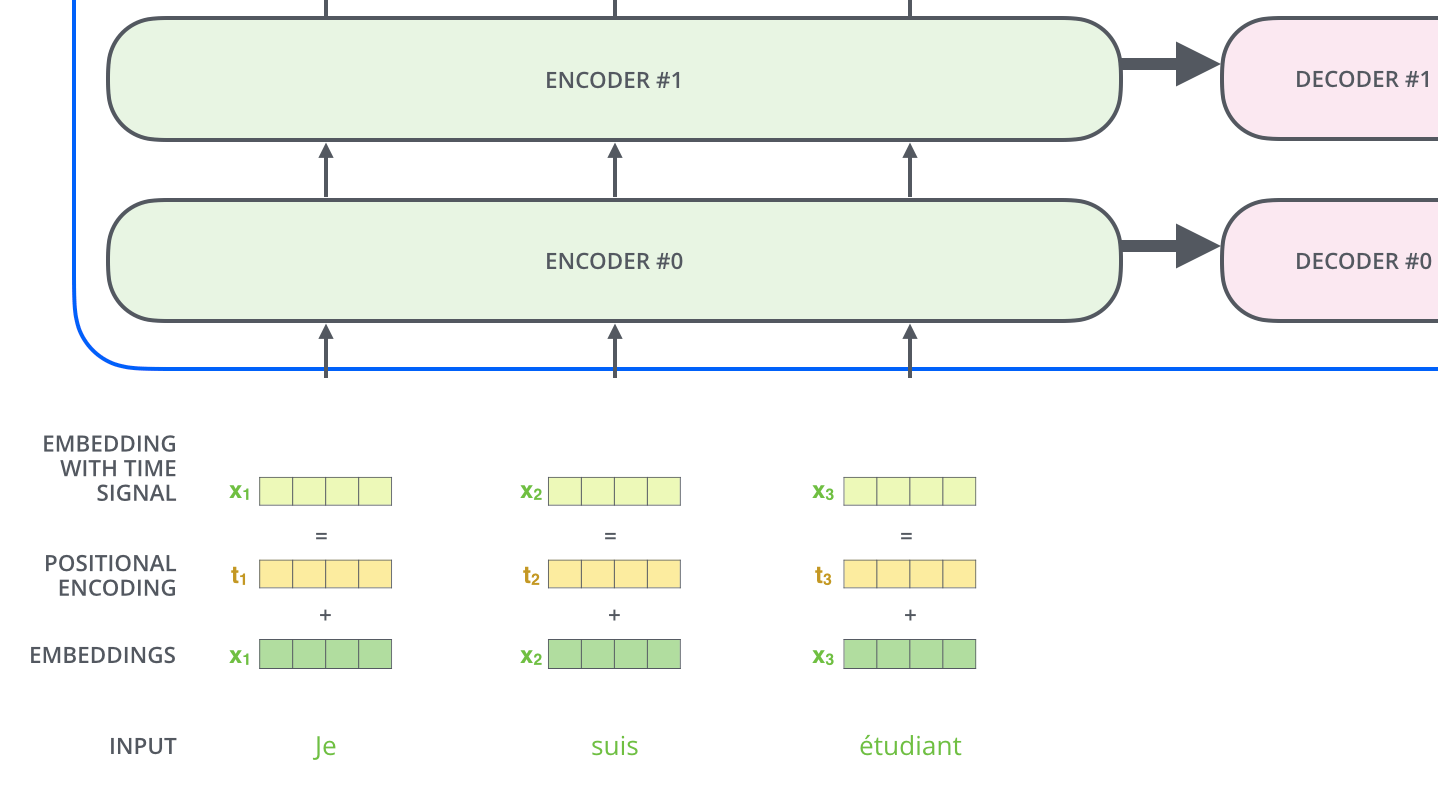
モデルに語順の情報を与えるために，特定のパターンに従った値を持つ位置エンコーディングベクトルを追加します。

埋め込みの次元数が4であると仮定すると，実際の位置エンコーディングベクトルの値は次のようになります。

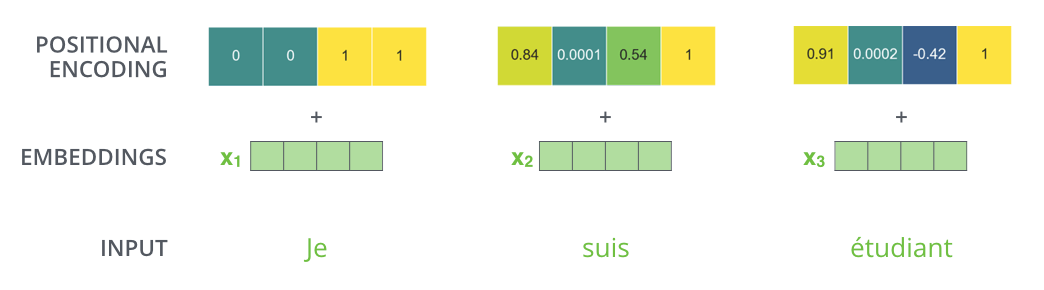
埋め込みサイズが4の位置符号化の実例

この模様は実際にはどんな風に見えるるのでしょうか？

次の図では，各行はベクトルの位置エンコーディングベクトルに対応しています。つまり，最初の行は入力系列の最初の埋め込みベクトルに追加するベクトルになります。各行には512個の値が含まれており，それぞれが1から-1までの値を持ちます。パターンが見えやすいように色分けしています。

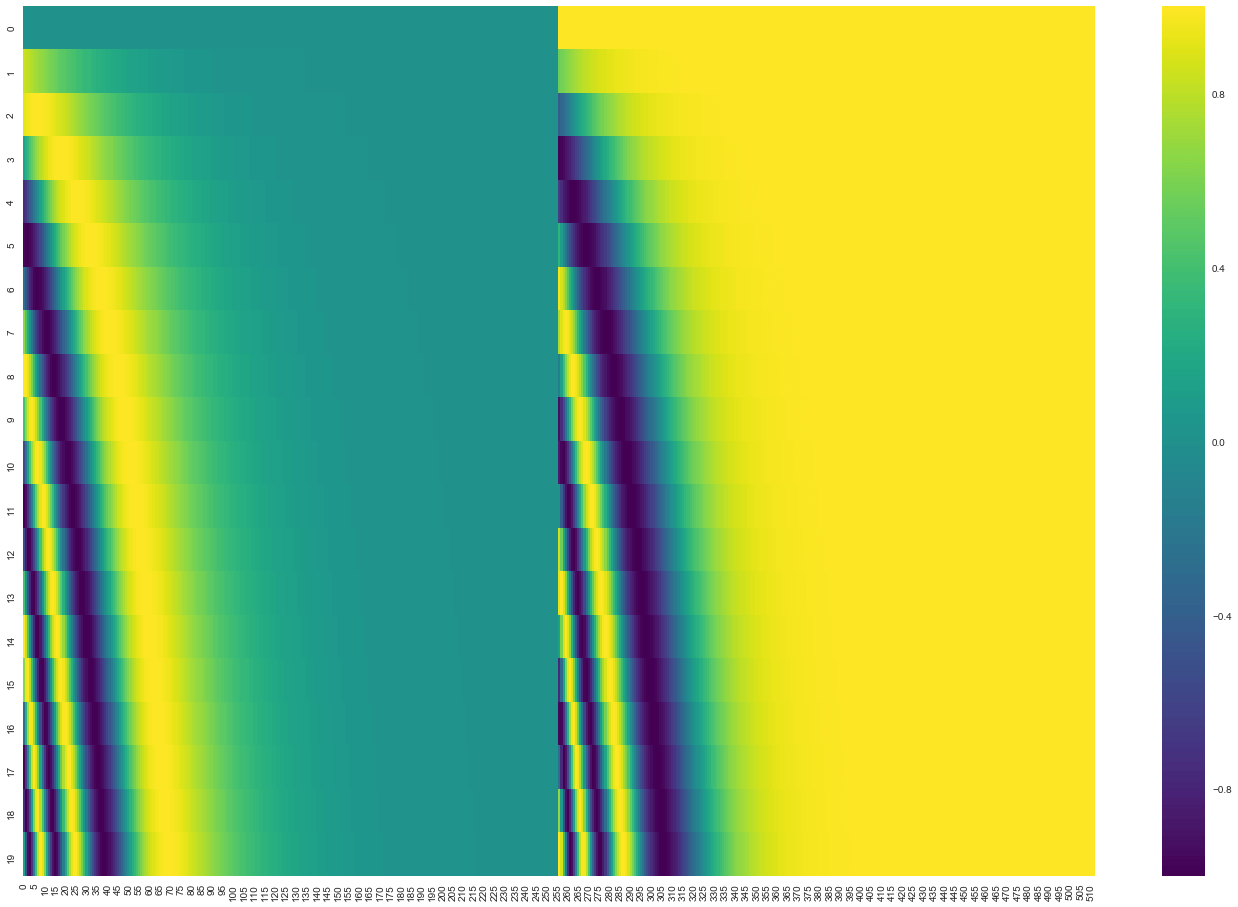
埋め込みベクトルの次元が512(列)，単語数が20(行)の位置エンコーディングベクトルの実例。中央を境にして半分に分かれて見えるのがわかります。これは，左半分の値がある関数（正弦波を使う）によって生成され，右半分の値が別の関数（余弦波を使う）によって生成されるからです。そして，それらを連結してそれぞれの位置エンコーディングベクトルを形成しています。

位置エンコーディングベクトルの計算式は論文の3.5節に記載されています。位置エンコーディングベクトルを生成するコードはget_timing_signal_1d()で確認することができます。これは，位置エンコーディングベクトルを計算するための唯一の方法ではありません。しかし，この方法は長さ不明の系列にもスケーリングできるという利点があります（例えば，学習済みモデルが学習データのどの文よりも長い文を翻訳することが求められた場合など）。

2020 7月 更新

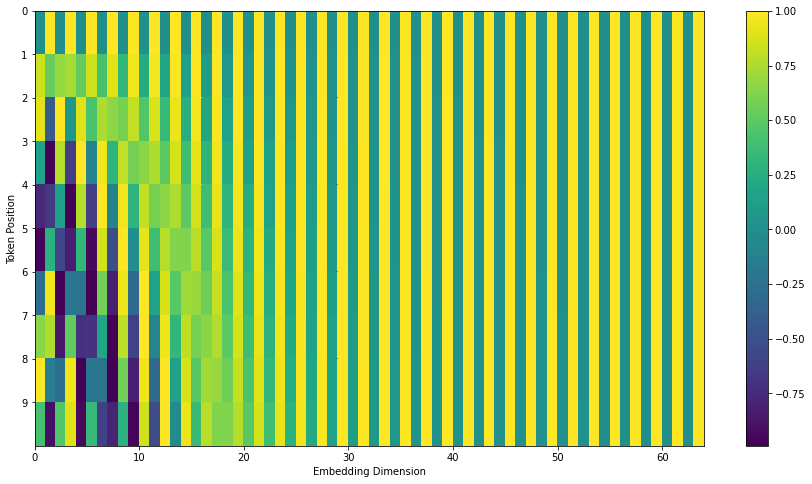
先ほどお見せした位置エンコーディングベクトルはTranformer2Transformerの実装に基づくものです。論文中で紹介されている位置エンコーディングは，先ほどのように左右にsin波とcos波を結合した形ではなく，埋め込みベクトルの次元方向にsin波とcos波を交互に出現させるものです。以下は後者の位置エンコーディングベクトルを可視化したのもです。実装はこちらに用意しています。

残差

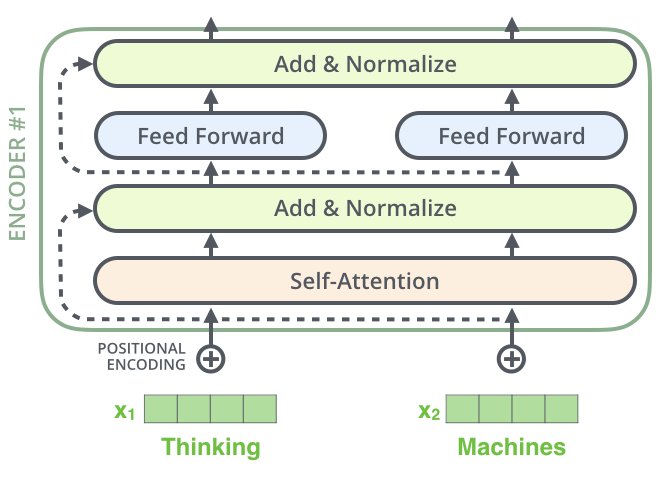
先に進む前に触れておく必要があるのですが，エンコーダのアーキテクチャでは，各サブレイヤ（自己注意層，全結合層）は，その周りに残差接続を持ち，正規化ステップが続いていることです。

自己注意に関連したベクトルと正規化の操作を可視化すると，次のようになります。

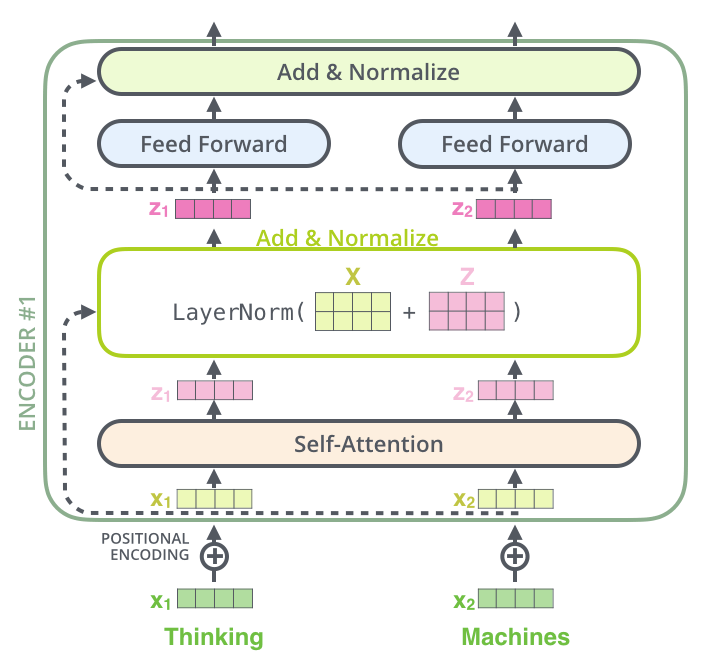
これはデコーダのサブレイヤにも当てはまります。２つのエンコーダとデコーダを積み重ねたトランスフォーマーを考えてみると，次のようになります。

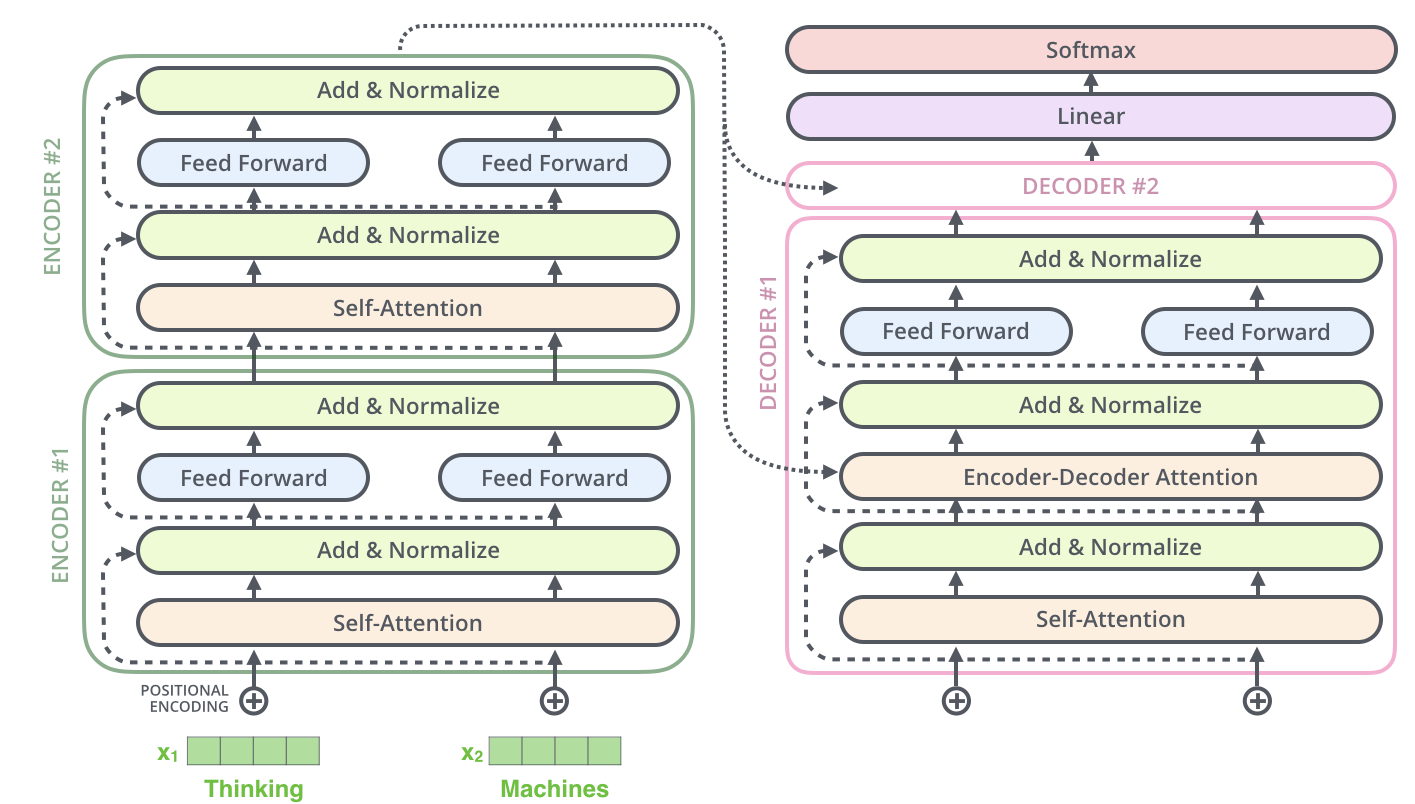
デコーダ側

ここまででエンコーダ側の概念をほとんど説明してきたので，皆さんは基本的にデコーダの構成要素がどのように動作するのかを知っています。しかし，ここではそれらがどのように連携して動作するのかを見てみましょう。

エンコーダは入力系列を処理することから始まります。最上段のエンコーダの出力は，続いてkeyベクトルとValueベクトルのセットに変換されます。これらは，各デコーダが「エンコーダ-デコーダ注意層」で使用するもので，デコーダが入力系列の適切な場所に注目するのに役立ちます。

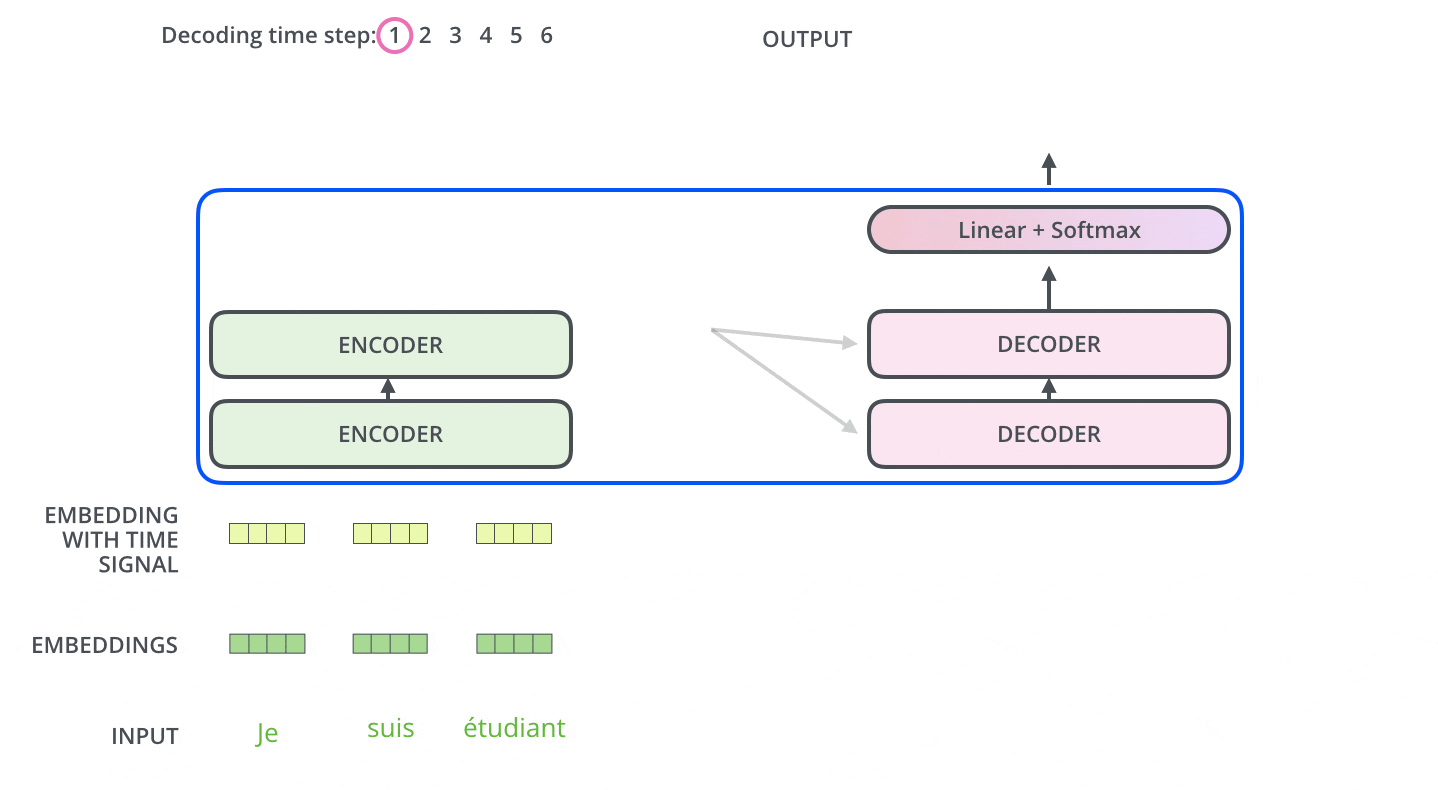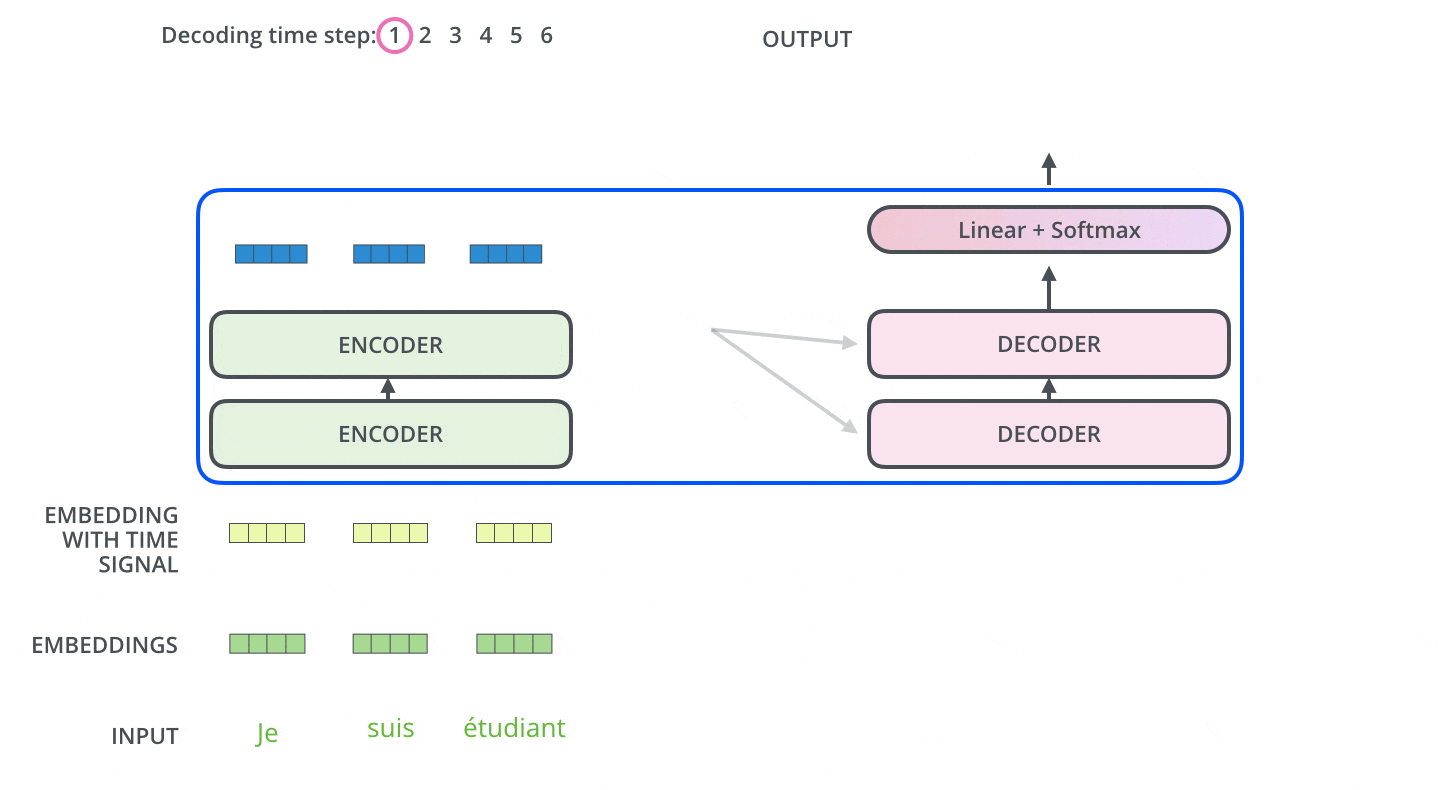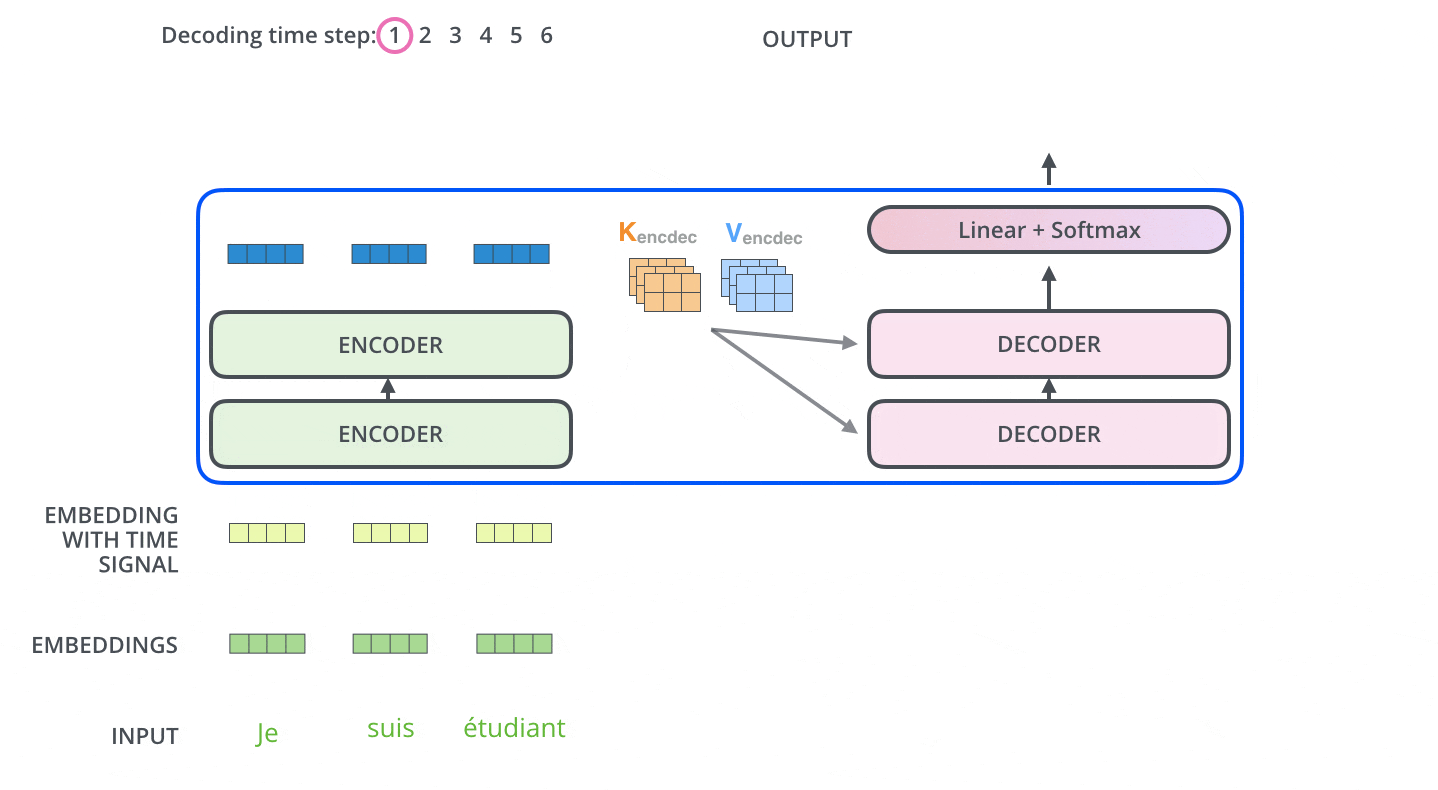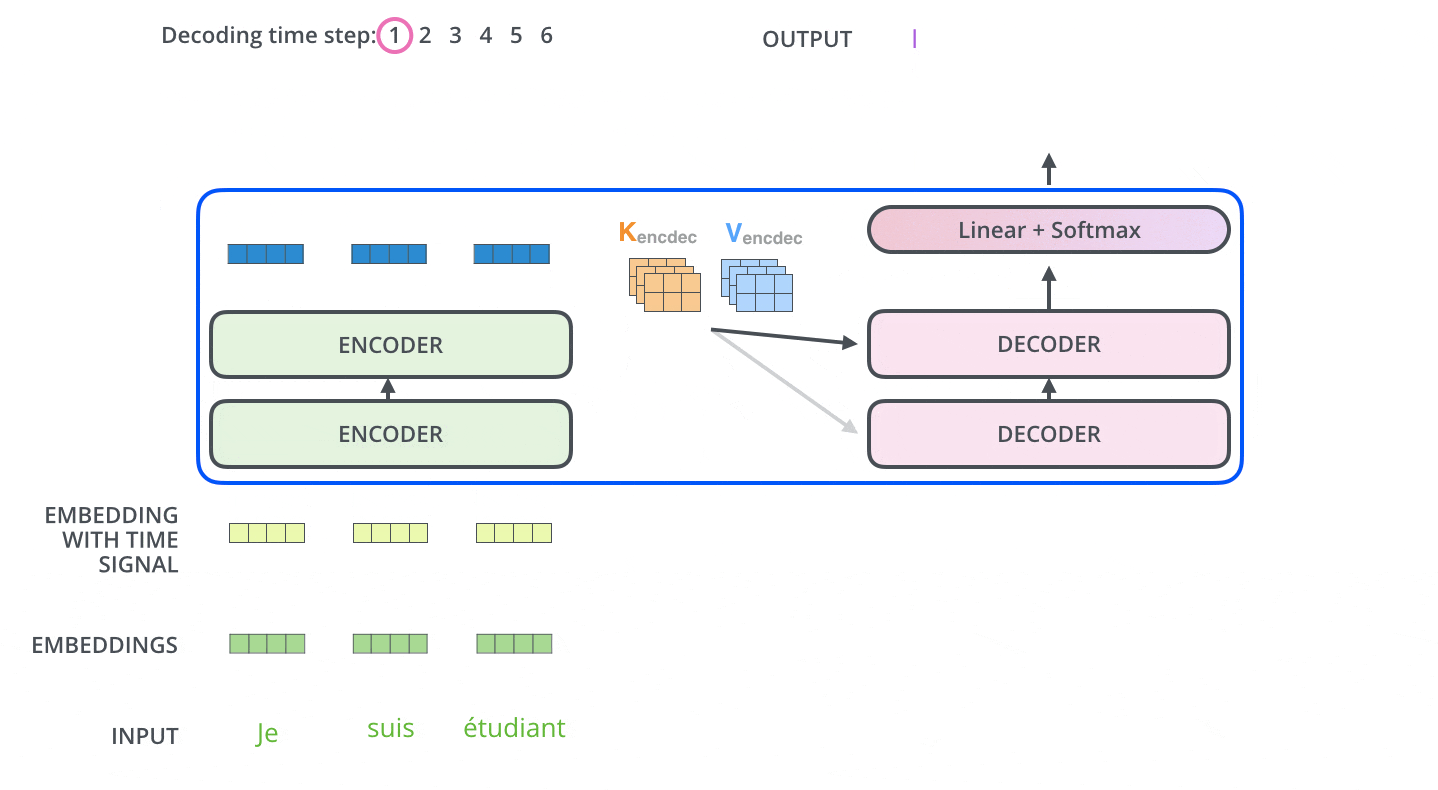
エンコーディングを終えた後に，デコーディングに入ります。デコーディングの各ステップでは，出力系列（ここでは英訳文）の内，１つの要素を出力します。

次のステップでは，Transformerのデコーダは，出力が完了したことを示す特別なシンボルに到達するまでプロセスを繰り返します。各ステップの出力は，次のタイムステップで最下段のデコーダに供給され，デコーダはエンコーダが行ったのと同様にデコード結果を上段のデコーダに送っていきます。その際，エンコーダの入力で行ったのと同じように，各単語の位置を示すためにデコーダの入力に位置エンコーディングベクトルを追加します。

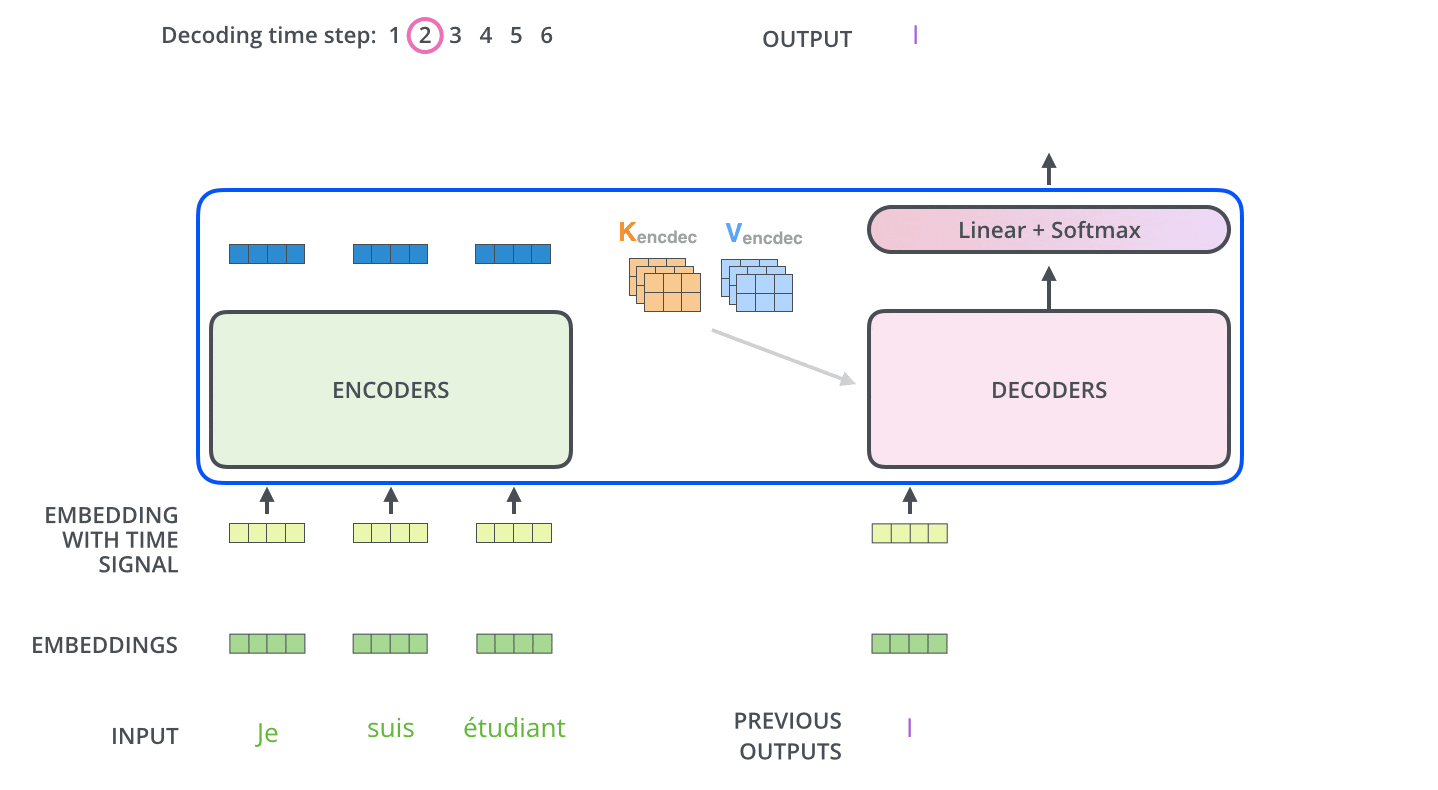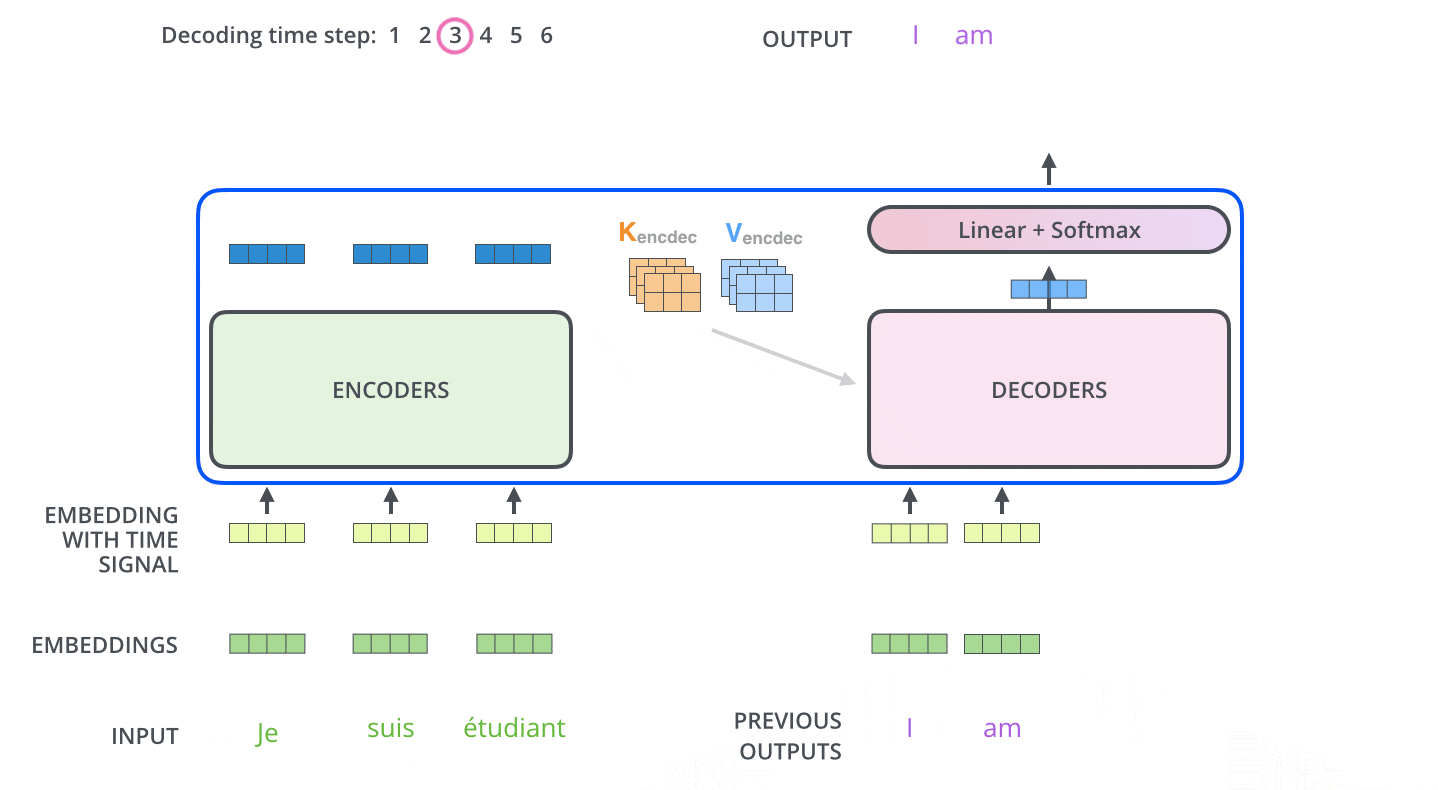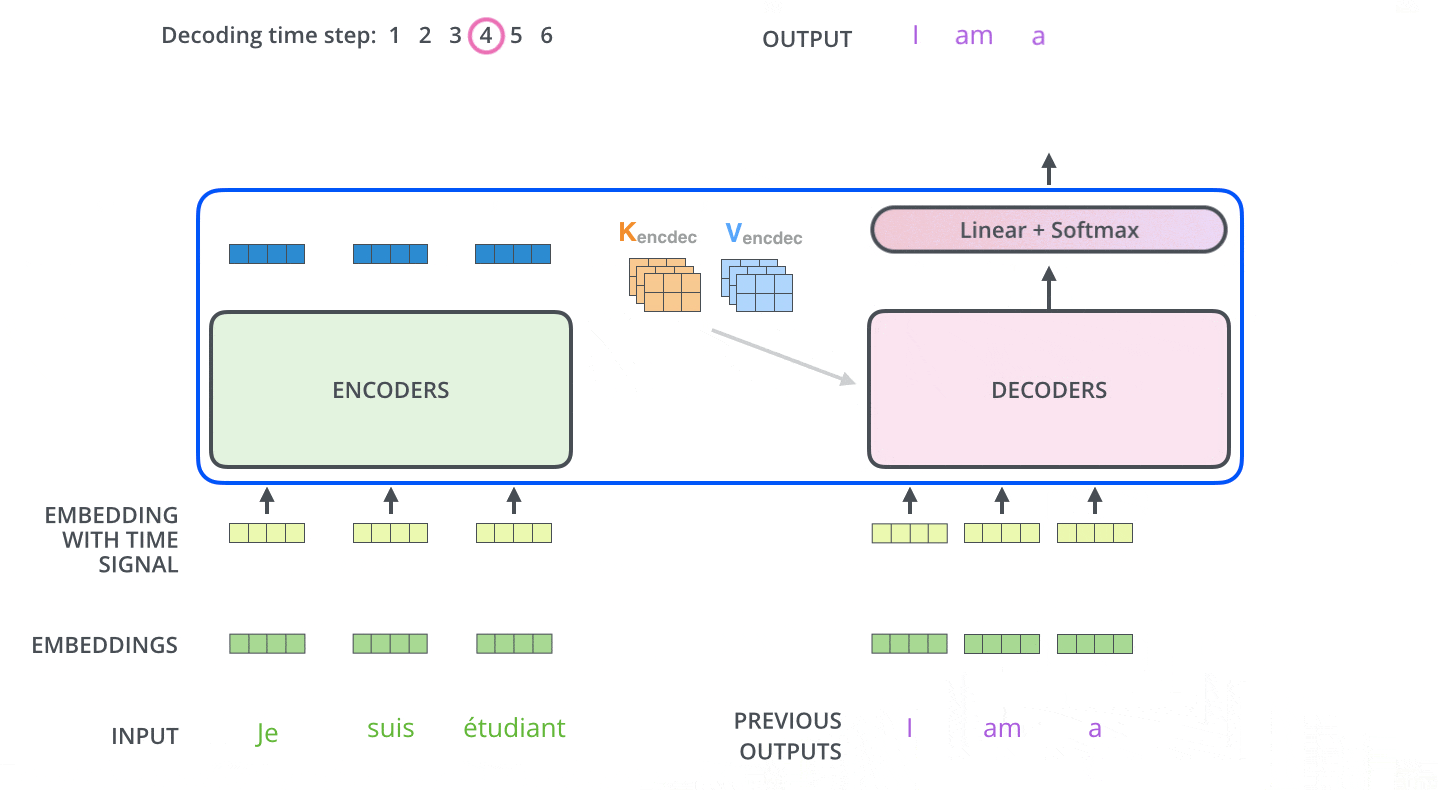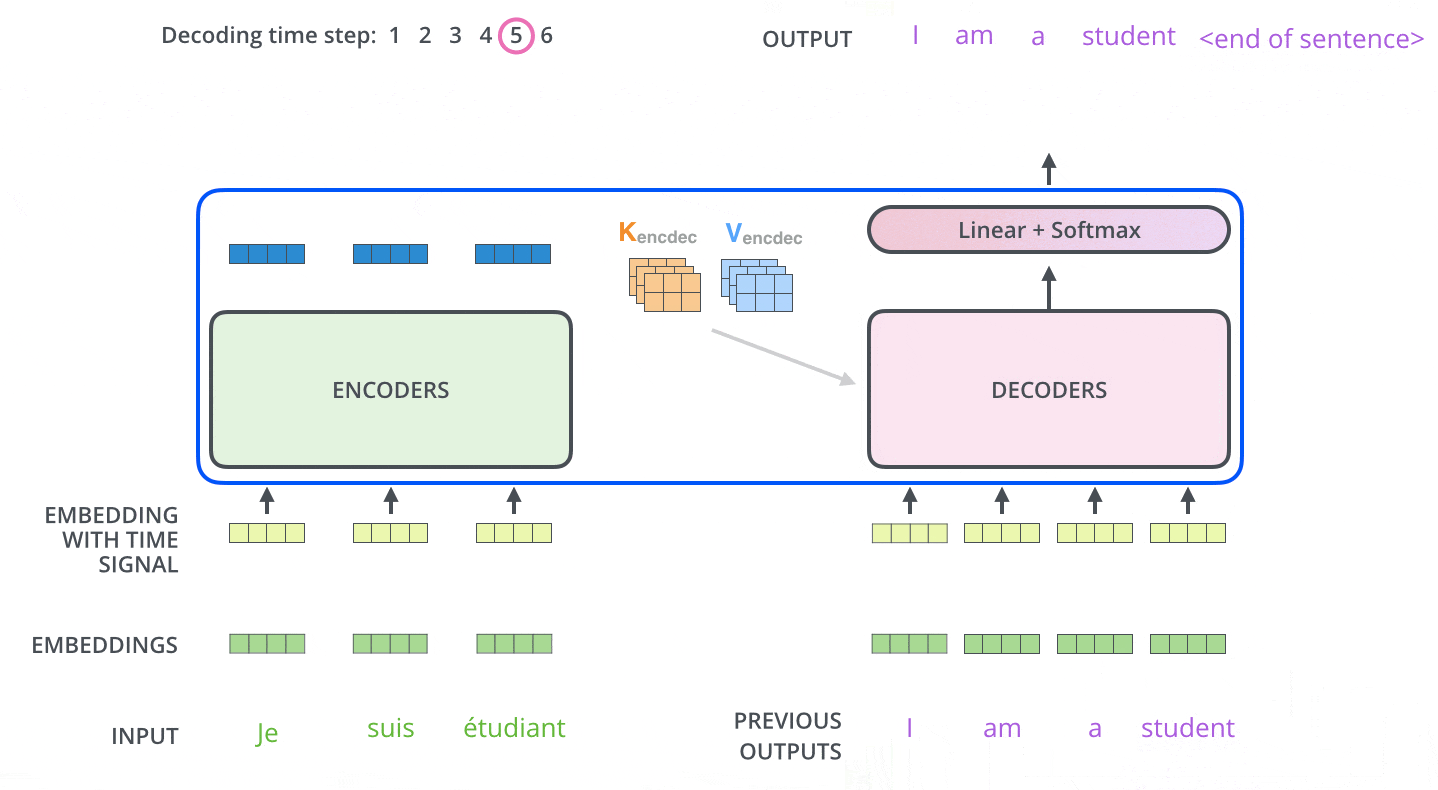
デコーダの自己注意層は，エンコーダの自己注意層とは少しだけ異なる方法で動作します。

デコーダでは，自己注意層は出力系列で処理している単語より前の位置にのみ注意を払うことができます。これは，自己注意計算のSoftmaxステップの前に，未来の位置をマスキング（実際は-infに設定）することで行われます。

最後の線形層とSoftmax層

積み重なったデコーダは，小数点の要素をもつベクトルを出力します。これをどうやって単語に変換するのでしょうか？これは最後の線形層とSoftmax層の仕事です。

線形層は単純な全結合ネットワークで，積み重なったデコーダから出力されたベクトルを，ロジットベクトルと呼ばれるもっと大きなベクトルに変換します。

あるモデルが，訓練データセットから10,000個の英単語（出力語彙）を学習したと仮定してみましょう。これにより，ロジットベクトルは10,000セルの幅になります。これが，モデルの出力を解釈する方法です。

Softmax層は，これらのスコアを確率に変換します（すべて正の値で，足して1になるように）。最も高い確率を持つセルが選択され，それに関連する単語がこの時間ステップの出力として生成されます。

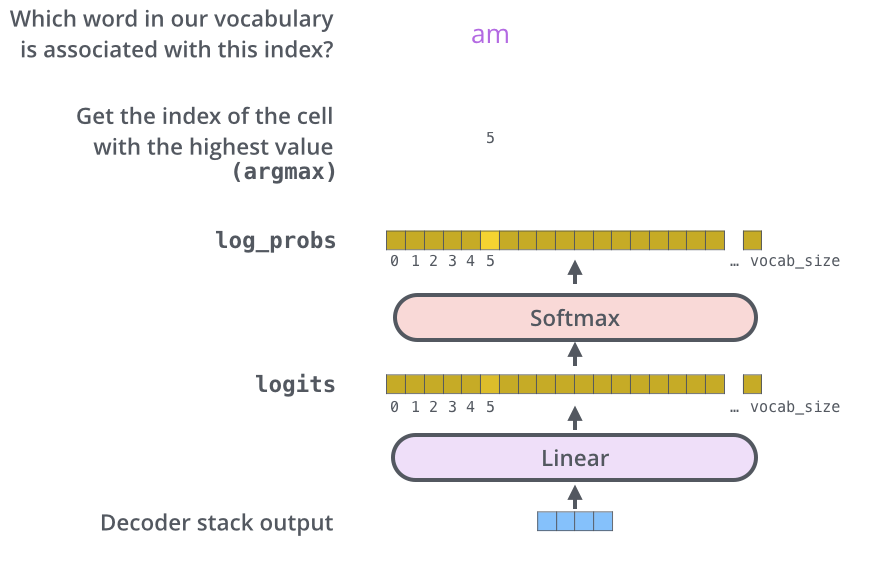
この図は，積み重なったデコーダの出力として生成されたベクトルが下から与えられて始まります。その後，出力する単語に変換されます。

学習の概要

学習済みのTransformerを通したプロセス全体を見てきたところで，今度はモデルを訓練する際のプロセスを直感的に少しだけ見てみると便利でしょう。

学習中のモデルは，上で見てきた学習済みモデルと全く同じパスを通過します。しかし，ラベル付けされた訓練データセットで学習しているので，その出力を実際のラベル付きデータと比較することができます。

これを可視化するために，出力語彙が6つの単語（”a”, “am”, “i”, “thanks”, “student”, “<eos>”（’end of sequence’の略））しか含まれていないと仮定してみましょう。

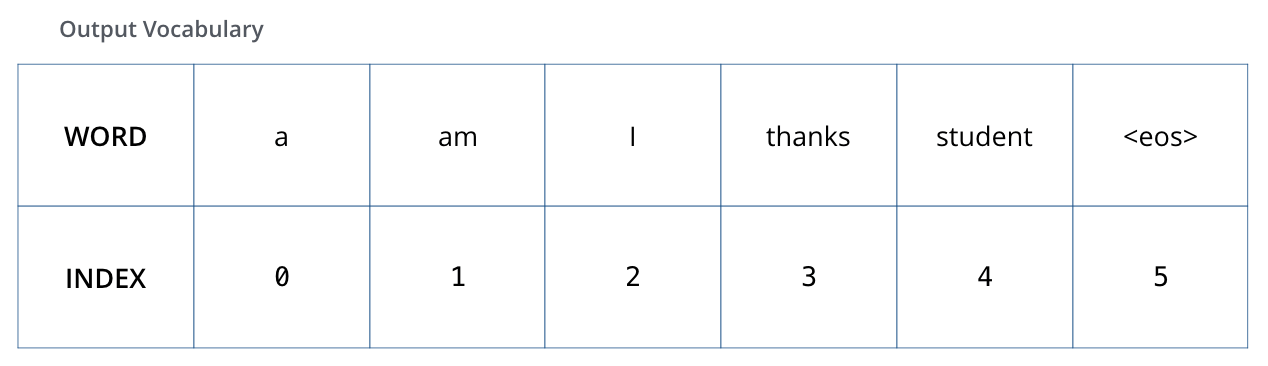
出力語彙は，学習を始める前の前処理段階で作成されます。

出力語彙を定義すると，語彙の各単語を示すために出力語彙と同じ幅のベクトルを使用することができます。これはワンホットエンコーディングとしても知られています。ですので，例えば次のようなベクトルを使って”am”という単語を示すことができます。

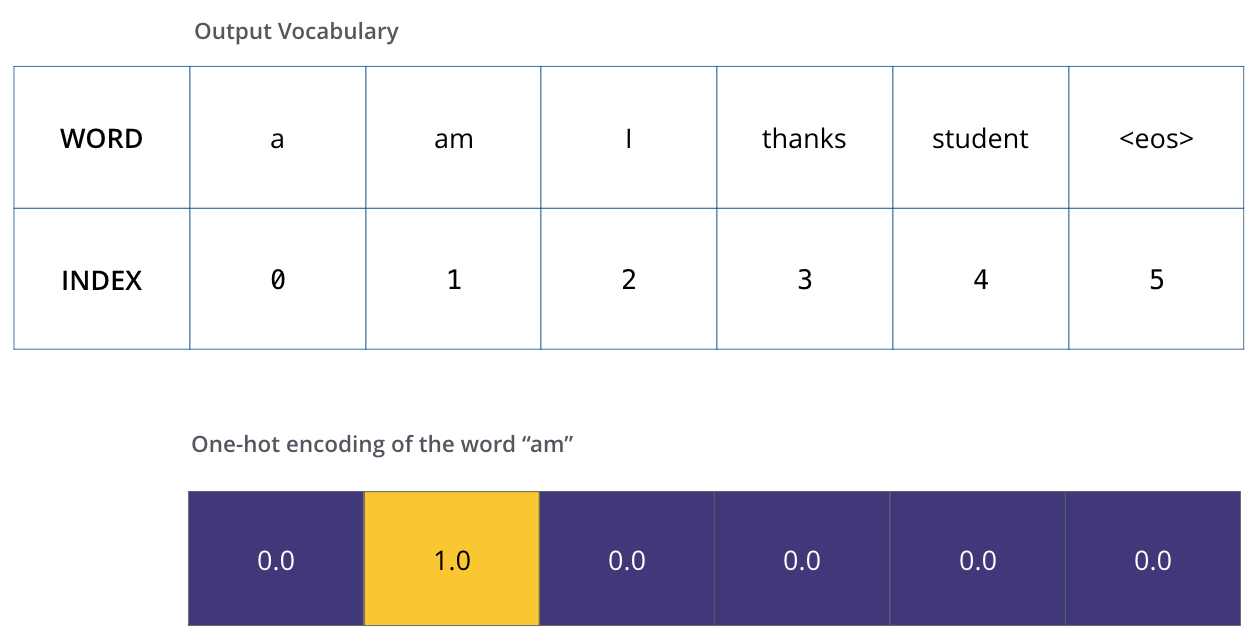
例：出力語彙のワンショットエンコーディング

ここまでの学習過程の概要に続いて，モデルの損失関数について説明していきます。つまり，学習段階でパラメータを最適化して，うまくいけば驚くほど正確なモデルにつながる仕組みについて説明します。

損失関数

モデルを学習しているとします。学習フェーズの最初のステップで，”merci”を “thanks”に翻訳するという単純な例で学習しているとしましょう。

この例が意味するのは，出力が “thanks”という単語を示す確率分布になるようにしたいということです。しかし，このモデルはまだ十分に学習されていないので，それはまだ起こりそうもありません。

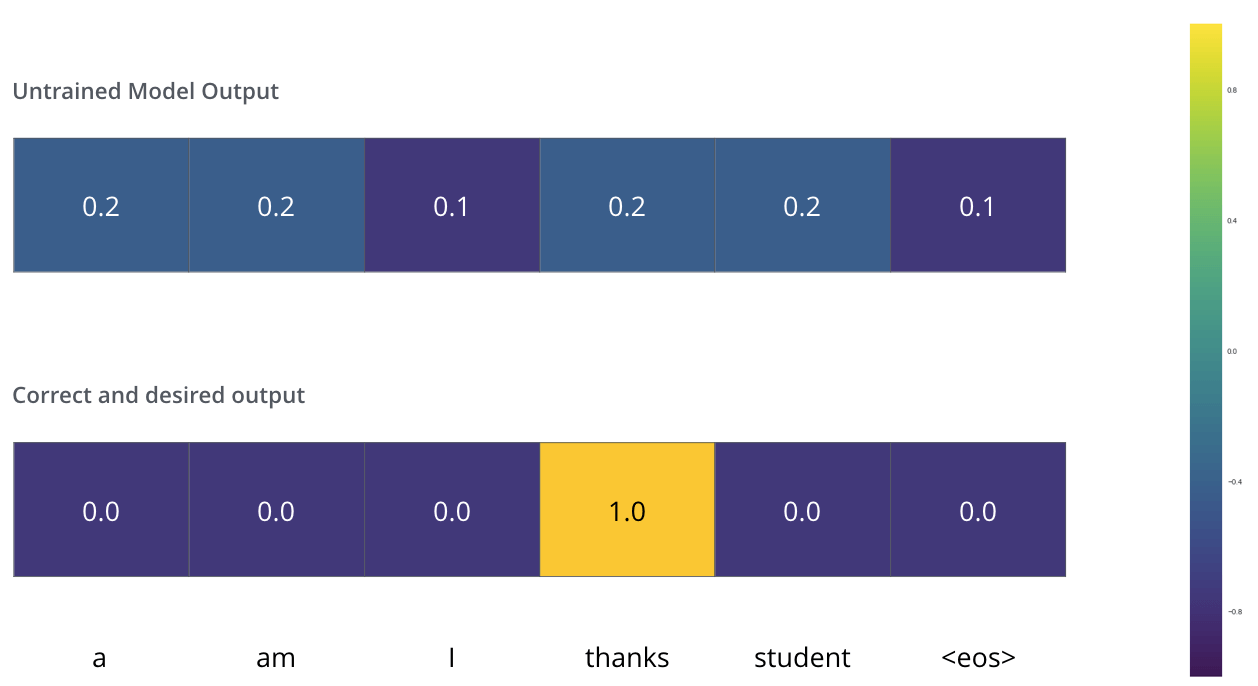
モデルのパラメータ（重み）がすべてランダムに初期化されているので，（非訓練の）モデルは各セル（単語）についてランダムな値を持つ確率分布を生成します。これを実際の出力と比較して，誤差逆伝播を使ってモデルのすべての重みを微調整して，出力を目的の出力に近づけることができます。

2つの確率分布を比較する方法ですか？単純に片方の確率分布をもう片方の確率分布から引くだけです。詳細については，クロスエントロピーとKullback-Leibler距離を参照してください。

しかし，これは過度に単純化された例であることに注意してください。より現実的には，１単語よりも長い文章を使います。例えば 入力は”je suis étudiant” で，期待される出力は”I am a student”という場合です。この例が実際に意味することは，我々のモデルが次のような確率分布を連続的に出力したいということです。

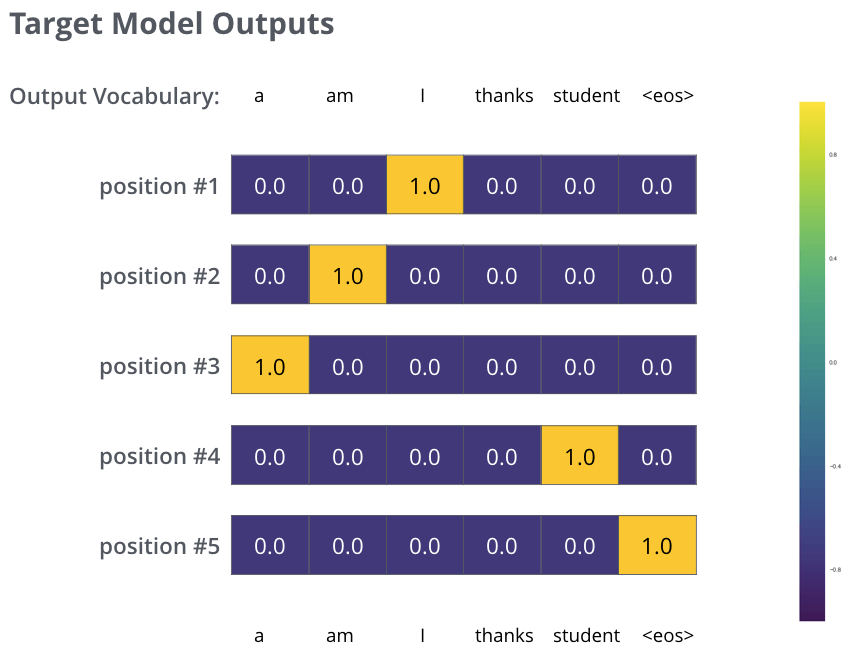
上記の例において，モデルを訓練する際に対象となる確率分布。

十分に大きなデータセットでモデルを十分学習した後には，生成された確率分布が以下のようになることを期待しています。

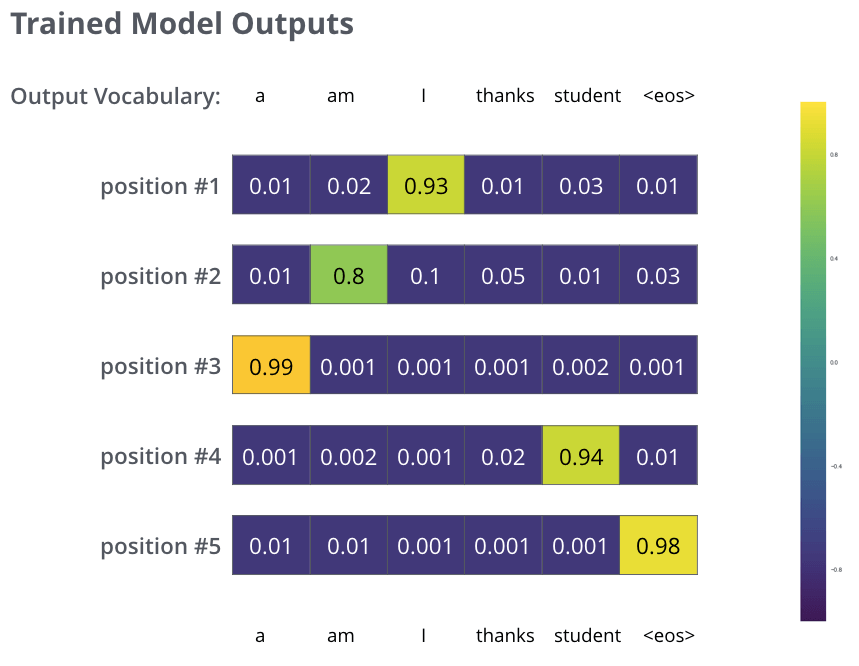
うまくいけば，学習時にモデルが期待される正しい翻訳を出力してくれます。もちろん，出力される単語列が訓練データセットの一部であるかどうかは実際のところわかりません（交差分割検証を参照してください）。すべての位置は，たとえそのタイムステップの出力する確率値が低くても出力されることに注目してください。これは，学習プロセスを助けるSoftmaxの非常に有用な特性です。

さて，モデルは１つずつ出力を生成するので，モデルはその確率分布から最も高い確率で単語を選択し，残りを捨てているとみなすことができます。これが１つの方法です（貪欲デコーディング）。別の方法としては，例えば，上位2つの単語（例えば’I’と’a’）を保持して，次のステップでモデルを2回実行します。1回目は最初の出力位置が単語’I’であると仮定し，もう1回目は最初の出力位置が単語’a’であると仮定し，位置#1と#2の両方を考慮してエラーが少ない方の単語列を保持します。これを位置#2と#3についても繰り返します。このメソッドは “ビームサーチ “と呼ばれ，今の例ではbeam_sizeは２（常に2つの部分的な仮説（未完成の翻訳）がメモリに保持されていることを意味します），top_beamsも2つ（2つの翻訳を返すことを意味します）です。これらはどちらも実験可能なハイパーパラメータです。

さらなる理解の助けに

本記事が，Transformerの主要概念を理解するために有益であること感じていただけましたでしょうか。もっと深く知りたい方には，次の内容をお勧めします。

その他手助けとなるリンク

---

翻訳はここまで

管理人コメント

私が思うに，世界で一番分かりやすいtransformerの説明だと思っています。今回は，Jay Alammarさんに許可をいただき，この素晴らしい記事を日本のみなさまに分かりやすい形で届けることを目的として翻訳致しました。ぜひ，参考にしていただければ幸いです。