本記事の内容は新ブログに移行されました。
こちらのブログにコメントをいただいても
ご返信が遅れてしまう場合がございます。
予めご了承ください。
ご質問やフィードバックは
上記サイトへお願い致します。
今回は，深層生成モデルの一種であるVAE(Variational Autoencoder)をPythonで実装する方法をお伝えしていこうと思います。
本記事はpython実践講座シリーズの内容になります。その他の記事は，こちらの「Python入門講座/実践講座まとめ」をご覧ください。また，本記事の実装は以下のサイトを参考にさせていただきました。ありがとうございます。
読みたい場所へジャンプ！
- VAEの概要
- ネットワークの構造
- VAEの学習（目的関数）
- 問題点
- よくある質問
- 質問1：モデルのどこに単位行列を仮定しているのか
- 質問2：式(1)の示す分布の正体
- 質問3：$p_{\theta}$の正体
- 質問4：「デコーダ$p_{\theta}$に関する分布は自分たちで定める必要がある」のに「$p_{\theta}(x)$は一般には計算できない」ことの説明
- 質問5：潜在変数の依存関係
- 質問6：関数とパラメータが同じであれば同じ分布なのか
- 質問7：エンコーダは高次元の空間から低次元の空間への射影なのか
- 質問8：エンコーダの操作は『低次元の空間へ埋め込み』とも呼ばれるのでしょうか。
- 質問9：潜在変数は等式で生成されるのでしょうか
- 質問10：ギブスサンプリングはやっぱり必要なんじゃないか
- 質問11：結局$p_{\theta}(\hat{x})$を知りたいってことじゃないの？
- 質問12：Decoderの出力分布がEncoderの入力分布を”忠実に”再現するように学習するってこと？
- 質問13：$p_{\theta}(\hat{x})=p_{\theta}(\hat{x}|z) p_{\theta}(z)$で目的関数が求められるのではないか
- 質問14：$p_{\theta}(x|z), p_{\theta}(z), p_{\theta}(x)$が同じ表記なのは混乱を招くだけでは？
- 質問15：$p_{\theta}(z)$は$q_{\phi}(z|x)$と同じなのではないか
- 質問16：$p_{\theta}(.)$は全て同じ構造を表しているのか
- 質問17：$p_{\theta}(.)$や$q_{\phi}(.)$はNN（ニューラルネットワーク）を表しているか
- 質問18：$p_{\theta}(.)$に関する分布を全て$p_{\theta}(.)$で表すのは分かりにくいのではないか
- 質問19：やはりデコーダ側のNNのパラメータ$\theta$が$z$に影響を与えるのは不可能なのではないか
- 質問20：再構成データはどのようにして生成されるのか
- 実装
- まとめ
VAEの概要
VAE（変分オートエンコーダ）とは，簡単にまとめると以下のような手法です。
●潜在変数モデルにおけるモデルエビデンスの推論方法の１つ
●入力を潜在空間上の特徴量で表す（エンコーダ）
●潜在空間から元の次元に戻す（デコーダ）
●潜在空間には何かしらの分布を仮定
潜在空間としては，分布のパラメータを設定します。例えば，潜在空間にガウス分布を仮定した場合，エンコーダでは潜在空間の「平均」と「分散」を学習するようにします。（出力ユニット数が２つのニューラルネットワークになるということです。）
ネットワークの構造
VAEのネットワークは「エンコーダ部」と「デコーダ部」に分かれます。よく勘違いされるのですが，VAEは「確率分布のパラメータ」を出力しているのであって，値そのものを出力しているわけではありません。
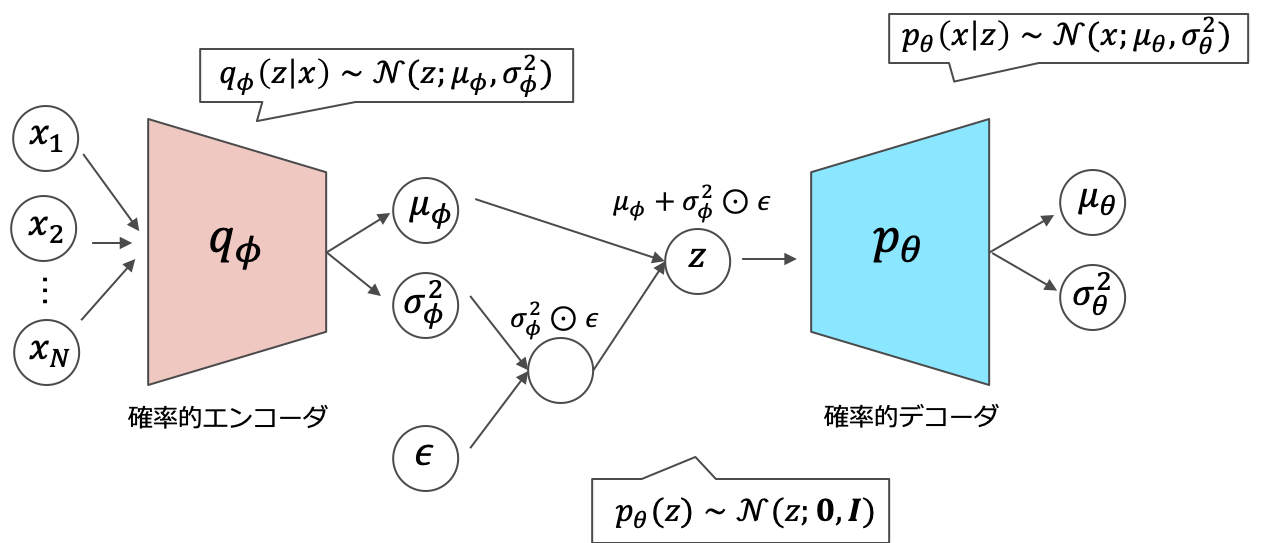VAEの構造一方で，デコーダ部に関しては再構成データをそのまま出力するモデルも存在します。一般にVAEと呼ぶときは，以下のネットワークを指していることが多いようです。MNISTなどで学習を行うときは，デコーダの出力はシグモイドにかけて[0,1]の値域にします。
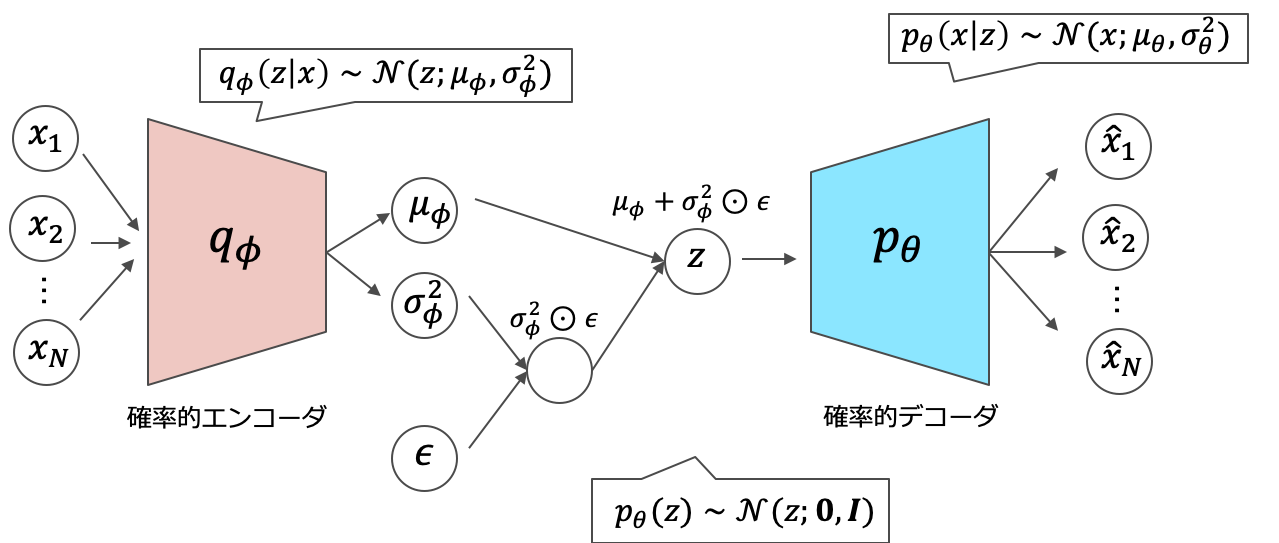VAEの構造バージョン2また，実用上以下のような分布の仮定を置くことが多いです。潜在空間には平均が$\boldsymbol{0}$で共分散行列が単位行列の標準多次元ガウス分布を仮定します。また，エンコーダ部にもガウス分布を仮定することで目的関数を解析的に求めることができます。（以下で説明します）
\begin{eqnarray}
q_{\phi}(\boldsymbol{z}|\boldsymbol{x}) &\sim& \mathcal{N}(\boldsymbol{z};\boldsymbol{\mu}_{\phi},\boldsymbol{\sigma^2}_{\phi})\\
p_{\theta}(\boldsymbol{z}) &\sim& \mathcal{N}(\boldsymbol{z};\boldsymbol{0},\boldsymbol{I})
\end{eqnarray}
大切なのは，デコーダ$p_{\theta}$に関する分布は自分たちで定める必要があるという点です。例えば，MNISTのような画像を対象とする場合は，ベルヌーイ分布を仮定してシグモイドを通すのが適しています。他には，音声のスペクトログラムなどを扱う場合は，デコーダ$p_{\theta}$にもガウス分布を仮定してしまいます。
VAEの学習（目的関数）
VAEの学習は，生成器$p_\theta(x)$の対数周辺尤度最大化です。しかし，$p_\theta(x)$は一般には計算できないため，潜在変数を噛ませて変分下界を最大化するという方向性で考えていきます。イエンセンの不等式より，変分下界の式を作ります。変分下界を$L(x; \varphi, \theta)$とおくことにします。
\begin{eqnarray}
\log p_\theta(x) &=& \log \int p_\theta(x, z) dz \\
&=& \log \int q_\varphi(z|x)\frac{p_\theta(x, z)}{q_\varphi(z|x)} dz \\
&\geq& \int q_\varphi(z|x) \log \frac{p_\theta(x, z)}{q_\varphi(z|x)} dz \\
&=& L(x; \varphi, \theta)
\end{eqnarray}
実は，変分下界（右辺）と対数周辺尤度（左辺）の差は識別器$q_\varphi (z|x)$と生成器$p_\theta (x|z)$のKLダイバージェンスになります。実際に計算してみると，以下のようになります。二つの項をくくり出すために積分して1になる$\int q_\varphi (z|x) dz$を持ち出す点がかなりトリッキーです。
\begin{eqnarray}
\log p_\theta(x) – L(x; \varphi, \theta) &=& \log p_\theta(x) – \int q_\varphi(z|x) \log \frac{p_\theta(x, z)}{q_\varphi(z|x)} dz \\
&=& \log p_{\theta}(x) \int q_{\varphi} (z|x) dz – \int q_{\varphi} (z|x) \log \frac{p_{\theta} (z|x)p(x)}{q_{\varphi}(z|x)} dz \\
&=& \int q_\varphi (z|x) \{ \log p_{\theta}(x) – \log p_\theta(z|x) – \log p_{\theta}(x) + \log q_\varphi (z|x) \} dz\\
&=& \int q_\varphi (z|x) \{ \log q_\varphi (z|x) – \log p_\theta(z|x) \} dz\\
&=& KL[q_\varphi (z|x) \| p_\theta (z|x)]
\end{eqnarray}
KLダイバージェンスは距離関数の一種で，必ず非負の値を取り，KLダイバージェンスが非負の値を取るため，結局対数周辺尤度を最大化することは，変分下界の最大化と等価になります。さて，変分下界を改めて計算し直してみましょう。（ベイズの定理を利用して$\log$で分解しています。）
\begin{eqnarray}
L(x; \varphi, \theta) &=& \log p_\theta(x) – KL[q_\varphi (z|x) \| p_\theta (z|x)] \\
\nonumber\\
&=& \log p_\theta(x) – E_{q_\varphi (z|x)}[\log q_\varphi(z|x) – \log p_\theta (z|x) ] \\
\nonumber\\
&=& \log p_\theta(x) – E_{q_\varphi (z|x)}[\log q_\varphi(z|x) – \log p_\theta (x|z) – \log p_\theta(z) + \log p_\theta (x)] \\
\nonumber\\
&=& E_{q_\varphi (z|x)}[\log p_\theta (x|z)] – KL[q_\varphi (z|x) \| p_\theta (z)]
\end{eqnarray}
変分下界を２つの項で表せましたね。期待値の方は，$p_\theta$（生成器）の分布を仮定してしまって計算すればOKです。例えば，二値画像の分類では出力は[0,1]であるので，生成器にベルヌーイ分布を仮定することが多いです。この場合，第1項目は以下のようになります。ただし，$f$は活性化関数を，$L$は潜在変数の次元を表しています。
\begin{eqnarray}
E_{q_\varphi (z|x)}[\log p_\theta (x|z)]
&=& E_{q_\varphi (z|x)}[\log \prod_l^{L} f(z_l)^x (1 – f(z_l))^{(1 – x)}] \\
&=& \frac{1}{L} \sum_{l=1}^L \{ x \log f(z_l) + (1 – x) \log (1 – f(z_l)) \}
\end{eqnarray}
上の式では，デコーダの出力の各次元$f(z_i)$に対して，ベルヌーイ分布を仮定しています。さらに，式（16）から（17）でモンテカルロ近似を利用しています。これは，次に，簡単に言えば期待値の積分計算を離散で有限サンプルの平均で表してしまおうという近似になります。
次に，KLダイバージェンスの方を考えてみましょう。こちら，真面目に計算すると非常に面倒臭いです。（$p_\theta (z)$と$q_\varphi (z|x)$に正規分布を仮定したとしても計算が煩雑になります）以下のPRML記事解説で計算過程はお伝えしていますので，参考にしていただければと思います。
以下では，文献[1]のAppendix Bにならって$p_\theta (z)$に$\mathcal{N}(\boldsymbol{z}; \boldsymbol{0}, \boldsymbol{I})$，$q_\varphi (z|x)$に$\mathcal{N}(\boldsymbol{z};\boldsymbol{\mu}, \boldsymbol{\sigma}^2)$を仮定します。結果は，このようになります。
\begin{eqnarray}
-KL[q_\varphi (z|x) \| p_\theta (z)]
&=& \frac{1}{2} \sum_{l=1}^L (1 + \log \sigma^2 – \mu^2 – \sigma^2)
\end{eqnarray}
以上をまとめると，変分下界は
\begin{eqnarray}
L(x; \varphi, \theta)
= &\frac{1}{L}& \sum_{l=1}^L \{ x \log f(z_l) + (1 – x) \log (1 – f(z_l)) \} \nonumber\\
&&+ \frac{1}{2} \sum_{l=1}^L (1 + \log \sigma^2 – \mu^2 – \sigma^2)
\end{eqnarray}
と書くことができます。こちらの変分下界を最大化することが，対数周辺尤度の最大化と等価になるのでした。実際の実装でも，こちらの式を計算しています。
問題点
と考えたあなた！まだまだ先があるんです…。よくよく考えてみると，エンコーダの出力は，どのようにして潜在変数のパラメータとして利用されるのでしょうか。
エンコーダは，潜在空間の分布のパラメータを出力しているわけですよね。そしたら，そのパラメータを利用して潜在空間を定義すればよいのでしょうか。もし，潜在空間を定義できたとしても，そこから$z$を得る作業（サンプリング）が必要になってしまいます。
Nooooです。サンプリングを行ってしまうと，誤差を逆伝播することが不可能になってしまうからです。ですから，$z$の値は決定的に定めなくてはなりません。そこで，編み出された妙案がこちらの式です。
\begin{eqnarray}
z = \mu + \epsilon \sigma
\end{eqnarray}
ただし，$\epsilon \sim \mathcal{N} (0, I)$とします。つまり，分布を仮定してサンプリングするのではなく，zというのは平均値にノイズ項を加えたものですよと近似してしまうというアイディアです。こちらの式は決定的に定まりますから，誤差の逆伝播を遮らずに済みます。ここが，VAEのアルゴリズムの中でも大切な部分です。
よくある質問
ここでは，本記事でいただいたご質問とその回答をまとめていきます。
質問1：モデルのどこに単位行列を仮定しているのか
デコーダの事前分布です。数式を用いれば，デコーダが条件付き確率で表される点がポイントです。つまり，デコーダは$p_{\theta}(x|z)$であって，$p_{\theta}(z)$はデコーダの事前分布です。また，エンコーダ・デコーダ型のモデルでは，デコーダの事前分布を「潜在空間」と呼ぶことが多いです。つまり，単位行列を仮定しているのはデコーダの事前分布（潜在空間）ということになります。本文中の式(2)です。
質問2：式(1)の示す分布の正体
式(1)は$q_{\phi}$に関する分布を定めていますので，エンコーダに関する分布です。これは，条件付き確率を意識すると分かりやすいと思います。つまり，$q_{\phi}(z|x)$は「$x$から$z$を生成する」と捉えればOKです。対して，条件付けられていない確率密度関数は事前分布を表すことが多いです。ここら辺は，ベイズ推論の考え方に通じるところがあります。以下の記事をぜひご参照ください。
●【初学者向き】ベイズ推論とは？事前分布や事後分布を分かりやすく解説してみます！
●【初学者向き】ベイズ推論の学習と予測とは？１次元ガウス分布を例に解説してみます！
●【これなら分かる！】変分ベイズ詳解＆Python実装。最尤推定/MAP推定との比較まで。
質問3：$p_{\theta}$の正体
$p_{\theta}$はデコーダに関する分布を表しています。デコーダの事前分布として$z$を考えるときに，$z$に関する分布の情報を加味する必要が出てきます。ここは少し頭が混乱するところですよね。$p_{\theta}$が吐き出す$x$は再構成された$\hat{x}$（のパラメータ）であることに注意が必要です。また，$p_{\theta}(x)$の分布は分かりません。なぜなら，それが分かればこんなに苦労してモデルを組み立てる必要がないからです。逆に言えば，最も汎用的にフィットするような$p_{\theta}(x)$を求めるのが私たちの目的です。
質問4：「デコーダ$p_{\theta}$に関する分布は自分たちで定める必要がある」のに「$p_{\theta}(x)$は一般には計算できない」ことの説明
日本語が下手くそでした…。確かに分かりにくいですね。「デコーダ$p_{\theta}$に関する分布」をより詳しく言えば「$p_{\theta}(x|z)$」と「$p_{\theta}(z)$」です。これらは，$p_{\theta}(x)$に潜在変数を噛ませてベイズの定理を利用することで，いわば無理やり「一般的には計算できない$p_{\theta}(x)$に関する裏の情報」を仮定しているわけです。このような背景から，「デコーダ$p_{\theta}$に関する分布は自分たちで定める必要がある」と記述しました。
質問5：潜在変数の依存関係
実は，潜在空間はエンコーダ・デコーダの両方に依存します。なぜなら，エンコーダでは$q_{\phi}(z|x)$，デコーダでは$p_{\theta}(z)$で$z$が分布の式に登場しているからです。若干語弊をうむことにはなりますが，基本的に分布は登場する変数に依存します（どれを主役に取るかの話）。
ただし，「条件付き確率」としての依存を指している場合は，デコーダに依存します。条件付き確率の右側に$z$が出てくるのはデコーダだけだからです。お答えとしては，条件付き確率として考える場合はデコーダのみに依存，VAEの原理として捉える場合は両方に依存します。
確かに$z$を生成するのはエンコーダの役割ですが，VAEの基本原理に立ち返ってみると「再構成誤差＋潜在空間の分布の良さ」を誤差関数として学習を回していきますので，$z$を変数として含むエンコーダ・デコーダに$z$は依存します。イメージとしては，エンコーダが入力を元にして潜在空間にデータをマッピングします。そして，マッピングされたデータを元にしてデコーダが入力と同じようなデータを再現します。このとき，「どれだけ入力と同じような出力がなされているか」と「どれだけエンコーダがマッピングした分布が標準正規分布（多次元）に近いか」によってVAEは学習していきます。これらは，両方とも$z$に依存しているため，VAEの原理として捉える場合は$z$はエンコーダ・デコーダの両方に依存するのです。
質問6：関数とパラメータが同じであれば同じ分布なのか
分布は必ずしも同じとは限りません。$p$と$q$は分布としては同じ種類ですが，各パラメータの値は異なります。つまり，母集団が従う分布の形は同じと仮定していますが，取ってきた結果はそれぞれ異なっているということです。
質問7：エンコーダは高次元の空間から低次元の空間への射影なのか
概ねその通りです！というのも，エンコーダ・デコーダ型のモデルの意義は，低次元の潜在空間への変換だからです。なぜ低次元に変換するのかというと，それだけ情報が凝縮され洗練されるからです。この操作をニューラルネットワークさんが勝手にしてくれるというのはかなり大きいです。従来は主成分分析を利用して行っていましたからね…。オートエンコーダが主成分分析の非線型変換であると捉えられているのもそのためです。逆に言えば，エンコーダ・デコーダ型のモデルで潜在空間を元の次元よりも大きくするようなモデルはあまり見かけません（エンコーダ・デコーダ型の良さを使えないモデルになってしまいます）。
質問8：エンコーダの操作は『低次元の空間へ埋め込み』とも呼ばれるのでしょうか。
正しい理解だと思います！ただ，埋め込みという用語はあまり使われない印象です。なぜなら，埋め込み（Embed）は専ら自然言語処理の分散表現に用いられる用語だからです。ここでは，変換という言葉をよく用いる印象を受けます。
質問9：潜在変数は等式で生成されるのでしょうか
はい。そういうことになります。ただし，本来であればエンコーダが出力したパラメータを元に$z$が自然に生成されるべきなのですが，本文中にもある通り「自然に生成される」というランダム操作を組み入れてしまうとニューラルネットワークの誤差伝播が途切れてしまいますので，等式「$=$」によって$z$を生成（決定）しています。これを「Reparameterization Trick」と呼び，VAEの発案者Kingma先生が考案された妙技です。
質問10：ギブスサンプリングはやっぱり必要なんじゃないか
ギブスサンプリングが要るか要らないか（使えるか使えないか）というのは，「モデルが誤差逆伝播によって学習しているかどうか」によって決められます。おっしゃる通り，解析的な数式によってモデル化できる場合はギブスサンプリングする必要はありません。ただし，ニューラルネットワークの枠組みではまた話は違ってきます。例えば，ベイズ推論で事前分布に共役事前分布を設定することが多いのは，解析的にパラメータの更新式を求めるためです。解析的に更新式が求まれば，サンプリングの必要はなくなります。しかし，今回のモデルはニューラルネットワークです。ベイズ推論とは学習の方法が異なりますので（深層ベイズモデリングは別として），ニューラルネットワークを誤差逆伝播で学習させる場合にはサンプリングという確率的な操作があってはならないのです。ですので，VAEではなくエンコーダ・デコーダ型のモデルを誤差逆伝播以外の方法で学習させる場合で，仮定した分布を解析的に解くことができないときには，おっしゃる通りサンプリングを利用するほかないと思います。しかし，このような状況はあまり起こりません。なぜなら，「サンプリングを行うしかない」という状況を作らないように研究者たちは努めているからです。
質問11：結局$p_{\theta}(\hat{x})$を知りたいってことじゃないの？
VAEの数式には$\hat{x}$は出現しません。なぜなら，VAEの基本的なモデリングはデコーダの出力が再構成データの分布の「パラメータ」であり，再構成データそのものではないからです。例えば，デコーダ$p_{\theta}$が入力データと全く異なるデータを出力したとしても，$p_{\theta}$を目的関数にしてしまえばデタラメなデコーダの出力を「尤もらしい」と判断するようなモデルが完成してしまい，オートエンコーダとして成り立たなくなってしまいます。VAEの正しい目的関数は$p_(x)$です。つまり，「デコーダ分布はどれだけ入力データを確からしいと判断できるか」がVAEの目的関数ということなのです。
質問12：Decoderの出力分布がEncoderの入力分布を”忠実に”再現するように学習するってこと？
こちらは，VAEの目的関数が$p_{\theta}(x)$であることに注意すれば分かりやすいと思います。イメージではほぼ同じように思えますが，VAEの目的関数は入力するデータの分布と出力されるデータの分布を近づけるような目的関数ではないです。つまり，「Decoderの出力分布がEncoderの入力分布を”忠実に”再現する」ように学習しているのではなく，「Decoderの分布がEncoderの入力をどれだけ確からしいと判断するか（確からしいと判断できるようにデコーダを形成するのがオートエンコーダ流派の基本思想です）」＋「潜在空間がどれだけ仮定した分布に近づいているか」の二つの項からVAEは学習されます。
質問13：$p_{\theta}(\hat{x})=p_{\theta}(\hat{x}|z) p_{\theta}(z)$で目的関数が求められるのではないか
こちらも，上述の通り$p_{\theta}(\hat{x})$の意味するところが不明になってしまいます。
質問14：$p_{\theta}(x|z), p_{\theta}(z), p_{\theta}(x)$が同じ表記なのは混乱を招くだけでは？
興味深い視点，ありがとうございます。この三者は同じ表記ではなくてはなりません。なぜなら，同じニューロンを通過しているからです。同じ重みパラメータ$\theta$を使って行列演算されているからです。ここは，ニューラルネットの特徴的な部分なのですが，対象を$x$にするのか$z$にするのか，はたまた$z$に条件づけられた$x$にするのかで，表す（裏に仮定される）分布が異なるように「できる」という点です。ニューラルネット，おそるべしです。ここを異なる表記にしてしまうと，対象が「$x$」なのか「$z$」なのか「$z$に条件づけられた$x$」なのかで，入力するニューロンが異なるように学習させなくてはならなくなってしまいます。
質問15：$p_{\theta}(z)$は$q_{\phi}(z|x)$と同じなのではないか
近い分布になると思います。なぜなら，この2つの分布を近づけることがVAEの目標の1つだからです。目的関数の片方の項は$KL[q_\varphi (z|x) \| p_\theta (z)]$ですね。これは2つの分布を近づけるようにVAEを学習しましょうという宣言に他なりません。
質問16：$p_{\theta}(.)$は全て同じ構造を表しているのか
確率変数によって表す分布は異なります。ネットワークのパラメータ$\theta$，$\phi$を利用するという状況下で，対象とする確率変数を変えれば表される分布も変わるような「上手い」パラメータを学習するのがキモです。
質問17：$p_{\theta}(.)$や$q_{\phi}(.)$はNN（ニューラルネットワーク）を表しているか
$p_{\theta}(.)$と$q_{\phi}(.)$は確率分布ですので，ニューラルネットワークとはそもそもの概念としての出発点が異なります。しかし，NNを入力-出力機構として捉えた場合に，ニューラルネットワークの入力と出力に様々な確率分布を仮定することができます。逆に，入力と出力に様々な確率分布を仮定することでニューラルネットワークを学習させることも可能になります。確率的にNNを発展させることにより，ベイズ推論のような議論も可能になります。
質問18：$p_{\theta}(.)$に関する分布を全て$p_{\theta}(.)$で表すのは分かりにくいのではないか
これはやはり，全て$p_{\theta}(.)$として表すことに意味があると私は思います。なぜなら，1つのエンコーダ・デコーダでVAEは構成されているからです。これが複数のエンコーダ・デコーダに拡張されれば，$r_{\omega}(.)$などと表記することになると思います。
質問19：やはりデコーダ側のNNのパラメータ$\theta$が$z$に影響を与えるのは不可能なのではないか
デコーダは$z$を入力として学習していきますので，入力の良さもデコーダのパラメータに影響を与えます。つまり，デコーダのパラメータ更新を行う中で$z$も対応して更新されていきます。
質問20：再構成データはどのようにして生成されるのか
本文中にあるVAEの図の1枚目のようにパラメータを出力する場合はサンプリングなどを利用します。これは，ネットワークの末端ですので誤差逆伝播には影響を与えません。2枚目のように再構成データそのものを出力する場合はデコーダの出力そのものが再構成データになります。
実装
以下では，MNISTを例にとって実装の各パートを眺めていきます。最後に全体のコードを載せたいと思います。
必要なライブラリのインポート
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from torch import optim
import torch.utils as utils
from torchvision import datasets, transformsチュートリアル通りだと思います。
deviceの定義
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")本記事では，GPUを利用する前提でコーディングしていきます。deviceを定義しておきましょう。
データセットのロード
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Lambda(lambda x: x.view(-1))])
dataset_train = datasets.MNIST(
'~/mnist',
train=True,
download=True,
transform=transform)
dataset_valid = datasets.MNIST(
'~/mnist',
train=False,
download=True,
transform=transform)
batch_size = 1000
dataloader_train = utils.data.DataLoader(dataset_train,
batch_size=batch_size,
shuffle=True,
num_workers=4)
dataloader_valid = utils.data.DataLoader(dataset_valid,
batch_size=batch_size,
shuffle=True,
num_workers=4)チュートリアル通りに読み込みます。
ネットワークの定義
class VAE(nn.Module):
def __init__(self, x_dim, z_dim):
super(VAE, self).__init__()
self.x_dim = x_dim
self.z_dim = z_dim
self.fc1 = nn.Linear(x_dim, 20)
self.bn1 = nn.BatchNorm1d(20)
self.fc2_mean = nn.Linear(20, z_dim)
self.fc2_var = nn.Linear(20, z_dim)
self.fc3 = nn.Linear(z_dim, 20)
self.drop1 = nn.Dropout(p=0.2)
self.fc4 = nn.Linear(20, x_dim)
def encoder(self, x):
x = x.view(-1, self.x_dim)
x = F.relu(self.fc1(x))
x = self.bn1(x)
mean = self.fc2_mean(x)
log_var = self.fc2_var(x)
return mean, log_var
def sample_z(self, mean, log_var, device):
epsilon = torch.randn(mean.shape, device=device)
return mean + epsilon * torch.exp(0.5*log_var)
def decoder(self, z):
y = F.relu(self.fc3(z))
y = self.drop1(y)
y = torch.sigmoid(self.fc4(y))
return y
def forward(self, x, device):
x = x.view(-1, self.x_dim)
mean, log_var = self.encoder(x)
delta = 1e-8
KL = 0.5 * torch.sum(1 + log_var - mean**2 - torch.exp(log_var))
z = self.sample_z(mean, log_var, device)
y = self.decoder(z)
# 本来はmeanだがKLとのスケールを合わせるためにsumで対応
reconstruction = torch.sum(x * torch.log(y + delta) + (1 - x) * torch.log(1 - y + delta))
lower_bound = [KL, reconstruction]
return -sum(lower_bound), z, yネットワークを「__init__」「_encoder」「_sample_z」「decoder」「forward」「loss」で定義しています。「__init__」にはdenseを利用した定義を，「_encoder」には潜在空間のパラメータを得るまでの定義を，「_sample_z」にはエンコーダで得たパラメータから$z$を計算するための処理を，「decoder」には$z$を入力として元の次元まで再現するネットワークの定義を，「forward」には実際の計算機構を，lossには上でお伝えした変分下界の定義を記述しています。
モデルの学習
model = VAE(x_dim=28*28, z_dim=10).to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)
model.train()
num_epochs = 20
loss_list = []
for i in range(num_epochs):
losses = []
for x, t in dataloader_train:
x = x.to(device)
loss, z, y = model(x, device)
model.zero_grad()
loss.backward()
optimizer.step()
losses.append(loss.cpu().detach().numpy())
loss_list.append(np.average(losses))
print("EPOCH: {} loss: {}".format(i, np.average(losses)))生成
fig = plt.figure(figsize=(20, 6))
model.eval()
zs = []
for x, t in dataloader_valid:
for i, im in enumerate(x.view(-1, 28, 28).detach().numpy()[:10]):
ax = fig.add_subplot(3, 10, i+1, xticks=[], yticks=[])
ax.imshow(im, 'gray')
x = x.to(device)
y, z = model(x)
zs.append(z)
y = y.view(-1, 28, 28)
for i, im in enumerate(y.cpu().detach().numpy()[:10]):
ax = fig.add_subplot(3, 10, i+11, xticks=[], yticks=[])
ax.imshow(im, 'gray')
z1to0 = torch.cat([z[1, :] * (i * 0.1) + z[0, :] * ((10 - i) * 0.1) for i in range(10)]).reshape(10, 10)
y2 = model._decoder(z1to0).view(-1, 28, 28)
for i, im in enumerate(y2.cpu().detach().numpy()[:20]):
ax = fig.add_subplot(3, 10, i+21, xticks=[], yticks=[])
ax.imshow(im, 'gray')
break
１行目がデータセットオリジナル。２行目は潜在空間から生成した画像。3行目は，2行目の０番目から１番目に割合を変えながら遷移させていったもの。徐々に７から４に移り変わっていることが読み取れます。また，以下のコードを用いれば潜在空間を可視化することができます。（[外部リンク]PyTorchでVAEのモデルを実装してMNISTの画像を生成する）
from sklearn.manifold import TSNE
from random import random
colors = ["red", "green", "blue", "orange", "purple", "brown", "fuchsia", "grey", "olive", "lightblue"]
def visualize_zs(zs, labels):
plt.figure(figsize=(10,10))
points = TSNE(n_components=2, random_state=0).fit_transform(zs)
for p, l in zip(points, labels):
plt.scatter(p[0], p[1], marker="${}$".format(l), c=colors[l])
plt.show()
model.eval()
zs = []
for x, t in dataloader_valid:
x = x.to(device)
t = t.to(device)
# generate from x
y, z = model(x)
z = z.cpu()
t = t.cpu()
visualize_zs(z.detach().numpy(), t.cpu().detach().numpy())
break
先ほど，７から４まで変化させていったときに，間に９のようなイメージが再現されました。これは，上の潜在空間でもみて取れると思います。７が集まっているゾーンから，４が集まっているゾーンに直線を引くと，９が集まっているゾーンを通りますね。
まとめ
VAEの簡単な理論的背景と実装をまとめてみました。理論は，ややトリッキーな点が何箇所かあるものの，全体的に分かりやすいモデルになっていると思います。GANと比べて出力が連続的になりやすいことは有名ですが，たしかに生成された画像はぼやけて見えますね。ラベル教師付きVAE（CVAE）にも注目が集まっていますね。
[1] Auto-Encoding Variational Bayes(https://arxiv.org/abs/1312.6114)
[2] PyTorchでVAEのモデルを実装してMNISTの画像を生成する
解説文も実装コードの例も大変素晴らしいで、
感謝の気持ちいっぱいです。
ただ、いくつかの質問をさせていただきたい
『潜在空間には平均が0で共分散行列が単位行列の標準多次元ガウス分布を仮定』これはデコーダによる潜在変数の生成においての分布ではなく、エンコーダの生成分布の共分散行列が『単位行列』ではと思いますが、ご説明お願い致します。
これは
その他の質問(1)：
式(1)からすれば、N分布の変数名がx(訓練データ)ですから、この分布は訓練データの分布だと思えますが、図からすればデコーダの出力になっているので、潜在変数zの分布か、εの分布だとも思えます。どっちでしょうか。
その他の質問(2)：
式(8)の中に二つの積分式が存在し、それそれの積分変数をdxとdzで表していますが、
式(9)の中にはdxもdzも消えてしまいました。
式(9)が生まれるプロセスを教えていただけませんか。
平均値で数学期待値を近似計算することがわかりますが、
logの性質から式(15)から(16)が生まれませんよね？
∵ log(a+b+c+…) ≠ log(a)+log(b)+log(c)+…
∴ (16)の生まれるプロセスをもう少しご説明お願い致します。
お世話になっております。
ごめんなさい！ またも質問です。
Q1：
pθは一体デコーダの出力xに関する分布であるか、それともエンコーダの出力zに関する分布でしょうか。
式(13)の中にpθ(z)とpθ(x)と同時に存在し、zとxが同じ分布でしょうか、
もし同じ分布であれば、pθ(z)～N(z; 0,I)に仮定したので、pθ(x)～N(x; 0,I) が自然に成立しますね。
そうであれば、わざわざpθ(x)を求める必要性もなくなるのではないでしょうか。
Q2：
『デコーダpθに関する分布は自分たちで定める必要がある』
『pθ(x)は一般には計算できない』
上記のような表現が同時に存在する事に不思議に思います。
もしpθが”自分たちで定める”のであれば、『pθ(x)は一般には計算できない』という話はないでしょう。
VAE初心者様
ご質問ありがとうございます。ひとつずつお答えしていきますね。
なお，以下は私の見解であるため，必ずしも正しいとは限らない点にご注意いただければと思います。
質問1：モデルのどこに単位行列を仮定しているのか
デコーダの事前分布です。数式を用いれば，デコーダが条件付き確率で表される点がポイントです。つまり，デコーダは$p_{\theta}(x|z)$であって，$p_{\theta}(z)$はデコーダの事前分布です。また，エンコーダ・デコーダ型のモデルでは，デコーダの事前分布を「潜在空間」と呼ぶことが多いです。つまり，単位行列を仮定しているのはデコーダの事前分布（潜在空間）ということになります。本文中の式(2)です。
質問2：式(1)の示す分布の正体
式(1)は$q_{\phi}$に関する分布を定めていますので，エンコーダに関する分布です。これは，条件付き確率を意識すると分かりやすいと思います。つまり，$q_{\phi}(z|x)$は「$x$から$z$を生成する」と捉えればOKです。対して，条件付けられていない確率密度関数は事前分布を表すことが多いです。ここら辺は，ベイズ推論の考え方に通じるところがあります。以下の記事をぜひご参照ください。
●【初学者向き】ベイズ推論とは？事前分布や事後分布を分かりやすく解説してみます！
●【初学者向き】ベイズ推論の学習と予測とは？１次元ガウス分布を例に解説してみます！
●【これなら分かる！】変分ベイズ詳解＆Python実装。最尤推定/MAP推定との比較まで。
質問3：式(9)が生まれるプロセス
こちらは記事に間違いがありました。修正いたしましたのでご確認ください。ご指摘誠にありがとうございます！
質問4：式(17)が生まれるプロセス
こちらも記事に間違いがございました…。$\log$を取る前は掛け算でした。ご確認ください。
質問5：$p_{\theta}$の正体
$p_{\theta}$はデコーダに関する分布を表しています。デコーダの事前分布として$z$を考えるときに，$z$に関する分布の情報を加味する必要が出てきます。ここは少し頭が混乱するところですよね。$p_{\theta}$が吐き出す$x$は再構成された$\hat{x}$であることに注意が必要です。慣習に従ってデコーダ$p_{\theta}$の出力を$x$と記述しましたが，ここは区別して記述しておくべきところだったかもしれません。$p_{\theta}(x)$の分布は分かりません。なぜなら，それが分かればこんなに苦労してモデルを組み立てる必要がないからです。逆に言えば，最も汎用的にフィットするような$p_{\theta}(x)$を求めるのが私たちの目的です。
質問6：「デコーダ$p_{\theta}$に関する分布は自分たちで定める必要がある」のに「$p_{\theta}(x)$は一般には計算できない」ことの説明
日本語が下手くそでした…。確かに分かりにくいですね。「デコーダ$p_{\theta}$に関する分布」をより詳しく言えば「$p_{\theta}(x|z)$」と「$p_{\theta}(z)$」です。これらは，$p_{\theta}(x)$に潜在変数を噛ませてベイズの定理を利用することで，いわば無理やり「一般的には計算できない$p_{\theta}(x)$に関する裏の情報」を仮定しているわけです。このような背景から，「デコーダ$p_{\theta}$に関する分布は自分たちで定める必要がある」と記述しました。
zuka 様
丁寧なご解説本当にありかとうございます。
『pθ(z)はデコーダの事前分布です。また，エンコーダ・デコーダ型のモデルでは，デコーダの事前分布を「潜在空間」と呼ぶことが多いです。つまり，単位行列を仮定しているのはデコーダの事前分布（潜在空間）ということになります。本文中の式(2)です』
分かりました。
潜在変数{z}はエンコーダから生成されたのですね、なので論理的にzの分布はエンコーダのパラメータΦに依存するはずで、どうして受け取る側としてのデコーダのパラメータθに依存するのでしょうか：pθ(z)にはθがあって、Φはないですね。
非常に鋭い質問ありがとうございます。
実は，潜在空間はエンコーダ・デコーダの両方に依存します。なぜなら，エンコーダでは$q_{\phi}(z|x)$，デコーダでは$p_{\theta}(z)$で$z$が分布の式に登場しているからです。若干語弊を産むことにはなりますが，基本的に分布は登場する変数に依存します（どれを主役に取るかの話）。ちなみに，なぜ$q_{\phi}(z)$がないのかの理由としては，エンコーダの事前情報に潜在空間がないからです。
ただし，「条件付き確率」としての依存を指している場合は，デコーダに依存します。条件付き確率の右側に$z$が出てくるのはデコーダだけだからです。お答えとしては，条件付き確率として考える場合はデコーダのみに依存，VAEの原理として捉える場合は両方に依存します。
確かに$z$を生成するのはエンコーダの役割ですが，VAEの基本原理に立ち返ってみると「再構成誤差＋潜在空間の分布の良さ」を誤差関数として学習を回していきますので，$z$を変数として含むエンコーダ・デコーダに$z$は依存します。イメージとしては，エンコーダが入力を元にして潜在空間にデータをマッピングします。そして，マッピングされたデータを元にしてデコーダが入力と同じようなデータを再現します。このとき，「どれだけ入力と同じような出力がなされているか」と「どれだけエンコーダがマッピングした分布が標準正規分布（多次元）に近いか」によってVAEは学習していきます。これらは，両方とも$z$に依存しているため，VAEの原理として捉える場合は$z$はエンコーダ・デコーダの両方に依存するのです。
ちなみに，潜在空間は必ずしもガウス分布が採用される訳ではないことに注意して下さい。最近では「潜在空間に多峰型のガウス分布を仮定しようぜ」という動きや，他の分布を仮定する研究も多く見られています。
本当にいい勉強になりました！
改めて感謝します。(知識のレベルにも感動的です)
最後ですが、概念的な事を確認させていただきます。ごめんなさいね！
(1)pθ(x),pθ(z),pθ(x|z)のように表現され、分布の関数名が同じで、分布のパラメータも同じですが、pθ(x),pθ(z),pθ(x|z)が同一分布（分布関数の形状が同じ）だと思うのは誤解ですね。
(2)『入力を元にして潜在空間にデータをマッピングします』
これは高次元の空間から低次元の空間への射影という事を意味するのでしょうか。あるいは『低次元の空間へ埋め込み』とも呼ばれるのでしょうか。
(3) 結局
z=μΦ＋(σΦ)^2⦿ε で潜在変数zを生成したのでしょうか
こちらこそご指摘ありがとうございます。参考になります。
質問(1)
分布は必ずしも同じとは限りません。$p$と$q$は分布としては同じ種類ですが，各パラメータの値は異なります。つまり，仮定している母集団は同じですが，取ってきた結果はそれぞれ異なっているということです。
質問(2)
>高次元の空間から低次元の空間への射影という事を意味するのでしょうか。
概ねその通りです！というのも，エンコーダ・デコーダ型のモデルの意義は，低次元の潜在空間への変換だからです。なぜ低次元に変換するのかというと，それだけ情報が凝縮され洗練されるからです。この操作をニューラルネットワークさんが勝手にしてくれるというのはかなり大きいです。従来は主成分分析を利用して行っていましたからね…。オートエンコーダが主成分分析の非線型変換であると捉えられているのもそのためです。逆に言えば，エンコーダ・デコーダ型のモデルで潜在空間を元の次元よりも大きくするようなモデルはあまり見かけません（エンコーダ・デコーダ型の良さを使えないモデルになってしまいます）。
>あるいは『低次元の空間へ埋め込み』とも呼ばれるのでしょうか。
正しい理解だと思います！ただ，埋め込みという用語はあまり使われない印象です。なぜなら，埋め込み（Embed）は専ら自然言語処理の分散表現に用いられる用語だからです。やはり，変換という言葉をよく用いる印象を受けます。
質問(3)
はい。そういうことになります。ただし，本来であればエンコーダが出力したパラメータを元に$z$が自然に生成されるべきなのですが，本文中にもある通り「自然に生成される」というランダム操作を組み入れてしまうとニューラルネットワークの誤差伝播が途切れてしまいますので，等式「$=$」によって$z$を生成（決定）しています。これを「Reparameterization Trick」と呼び，VAEの発案者Kingma先生が考案された妙技です。
① オートエンコーダは非線形的な『主成分分析(PCA)』に相当
② 潜在変数zの生成は自分の想像に反して、ニューロン端子でなく、直接数式で算出した
どうもありがとうございました！！
面白いので、 zuka 様にまたお伺いしたいです。 ＾_＾;
> ああ！ギブスサンプリングとか使えばええんちゃう？
> Nooooです。
” Noooo”には異議ありますね。
自分の理解では、Pθ(z)をGaussian N(0,1)に指定されたこそ初めて ギブスサンプリングが要らなくなるのです。
というのは、Gaussian N(0,1)や一様分布の場合、分布に従う確率変数を解析的な数式より構造する事ができるためです。
一般的に、任意の分布を指定して高次元の確率変数を構造するのに z=μ+σ*ε のようにできないでしょう。
なので、Pθ(z)を任意の分布に指定したいなら、やはりギブスサンプリングを利用して確率変数としてのvectorを生成するしかないのでは、と思いますが、
ご意見をお願い致します。
ご質問ありがとうございます。
>$p_{\theta}(z)$を$\mathcal{N}(0,1)$に指定されたこそ初めてギブスサンプリングが要らなくなる
ギブスサンプリングが要るか要らないか（使えるか使えないか）というのは，「モデルが誤差逆伝播によって学習しているかどうか」によって決められます。おっしゃる通り，解析的な数式によってモデル化できる場合はギブスサンプリングする必要はありません。ただし，ニューラルネットワークの枠組みではまた話は違ってきます。例えば，ベイズ推論で事前分布に共役事前分布を設定することが多いのは，解析的にパラメータの更新式を求めるためです。解析的に更新式が求まれば，サンプリング（もちろんギブスサンプリングも）の必要はなくなります。しかし，今回のモデルはニューラルネットワークです。ベイズ推論とは学習の方法が異なりますので，ニューラルネットワークを誤差逆伝播で学習させる場合にはサンプリングという確率的な操作があってはならないのです。ですので，VAEではなくエンコーダ・デコーダ型のモデルを誤差逆伝播以外の方法で学習させる場合で，仮定した分布を解析的に解くことができないときには，おっしゃる通りサンプリングを利用するほかないと思います。しかし，このような状況はあまり起こりません。なぜなら，「サンプリングを行うしかない」という状況を作らないように研究者たちは努めているからです。
> $p_{\theta}(z)$を任意の分布に指定したいなら，やはりギブスサンプリングを利用して確率変数としてのvectorを生成するしかない
上述の通り，VAEではないモデルの場合には正しい主張だと思います！
益々立派なドキュメントになりましたね！
VAEに関して、並大抵の紹介文章があるものの、丁寧に解説され、掘り下げて議論される処が少ないだけに、意義があると思います。
嵌りました！ お助けていただければ幸です。
私の認識では、VAEの思想脈絡として：
pθ(x’)を知りたい、そして pθ(x’) = qΦ(x)にしたい (xはEncoderの入力で x’はDecoderの出力で、xに対する再現。簡単のために、x’がxで表される場合もある)。
上記によってDecoderの出力空間分布がEncoderの入力空間分布を”忠実に”再現されるという意味で、
理想なEncoder-Decoderシステムになります。
【data/sampleの空間分布：時にはManifold(の構造)とも呼びます】
それに、
pθ(x’) = pθ(x’|z)*pθ(z)
pθ(x’|z)はDecoderで,”whose distribution parameters are computed from z with a MLP”(Auto-EncodingVariationalBayes
原文より)
これで、pθ(x’)が求められる事になり、どうしてpθ(x’)を見積もるためにlow bound L(…)関数を導入する必要があるのでしょうか。
言い間違ったら、ご指摘お願い申し上げます。
⇓ 混乱の元？
pθ(x|z)
pθ(z)
pθ(x)
この三者が同じ関数名で表記されるのは初心者にとって概念的な混乱を齎しやすいのでは？
pθ(x)は基本は未知として最終的にqΦ(x)に収束するのが理想とします。
pθ(z)は所謂decoderの”事前分布”で、人間指定・仮定可能。
pθ(x|z)はdecoderの学習によって生成されます。
三者はまったく別々の概念で、θが分布のパラメータではなく、NNのパラメータであり、三者の関数形状が同一ではありません ⇨ 異なるmanifold構造を反映しています。ただ、pθ(z)とpθ(x|z)はおおざっぱに皆Gassian分布であるのを仮定できます。（「Gassian分布」と言っても、形状が色々あります）
ごめんなさい
Gassian ⇨ Gaussian
もっと言えば、
pθ(z)はqΦ(z|x)によって形成した(μΦを中心とし、分散がσΦである)分布の集合に構成された分布(マクロ)だと思いますね。イメージとして無数の円心が0でない小円によって円心が0にある大きな円を張ったような感じです。この円はGaussian分布のドメインに相当します。
当然pθ(z)=N(0,I)に仮定可能です。
ご質問ありがとうございます。
申し遅れましたが，これらのやり取りは本文に記載させていただいておりますのでご了承ください！
質問1：$p_{\theta}(\hat{x})$を知りたい？
こちら，先日の議論に誤りがありました。「慣習に従ってデコーダ$p_{\theta}$の出力を$x$と記述しましたが，ここは区別して記述しておくべきところだったかもしれません」という部分がまずかったです。やはり，VAEの数式には$\hat{x}$は出現しません。なぜなら，VAEの基本的なモデリングはデコーダの出力が再構成データの分布の「パラメータ」であり，再構成データそのものではないからです。正しくは$p_{\theta}(x)$です。つまり，「デコーダ分布はどれだけ入力データを確からしいと判断できるか」がVAEの目的関数ということなのです。
質問2：Decoderの出力分布がEncoderの入力分布を”忠実に”再現する
こちらは，VAEの目的関数が$p_{\theta}(x)$であることに注意すれば分かりやすいと思います。イメージではほぼ同じように思えますが，VAEの目的関数は入力するデータの分布と出力されるデータの分布を近づけるような目的関数ではないです。つまり，「Decoderの出力分布がEncoderの入力分布を”忠実に”再現する」ように学習しているのではなく，「Decoderの分布がEncoderの入力をどれだけ確からしいと判断するか（確からしいと判断できるようにデコーダを形成するのがオートエンコーダ流派の基本思想です）」＋「潜在空間がどれだけ仮定した分布に近づいているか」の二つの項からVAEは学習されます。
質問3：$p_{\theta}(\hat{x})=p_{\theta}(\hat{x}|z) p_{\theta}(z)$で目的関数が求められるのではないか
こちらも，上述の通り$p_{\theta}(\hat{x})$の意味するところが不明になってしまいます。例えば，デコーダ$p_{\theta}$が入力データと全く異なるデータを出力したとしても，$p_{\theta}$を目的関数にしてしまえばデタラメなデコーダの出力を「尤もらしい」と判断するようなモデルが完成してしまい，オートエンコーダとして成り立たなくなってしまいます。
質問4：$p_{\theta}(x|z), p_{\theta}(z), p_{\theta}(x)$が同じ表記なのは混乱を招くだけでは？
興味深い視点，ありがとうございます。この三者は同じ表記ではなくてはなりません。なぜなら，同じニューロンを通過しているからです。同じ重みパラメータ$\theta$を使って行列演算されているからです。ここで，ニューラルネットの強い部分なのが，対象を$x$にするのか$z$にするのか，はたまた$z$に条件づけられた$x$にするのかで表す（裏に仮定される）分布が異なるように「できる」という点です。ここを異なる表記にしてしまうと，対象が$x$なのか$z$なのか$z$に条件づけられた$x$なのかで入力するニューロンが異なるように学習させなくてはならなくなってしまいます。
質問5：$p_{\theta}(z)$は$q_{\phi}(z|x)$と同じなのではないか
近い分布になると思います。なぜなら，この2つの分布を近づけることがVAEの目標の1つだからです。目的関数の片方の項は$KL[q_\varphi (z|x) \| p_\theta (z)]$ですね。これは2つの分布を近づけるようにVAEを学習しましょうという宣言に他なりません。
非常に素晴らしいご解説有難うございます！
なお、自分とzuka 様の間に概念的なずれがあるかどうかを確認したいのです。
＊＊＊＊＊私の場合：
私はpθ(..)やqΩ(..)を分布として理解しています。
このpは他ならぬprobabilityのpだと思います。
ただ、この関数はMLPによって実現されたのでMLPのパラメータθ/Ωで脚注しています。
しかし、θ/Ωは分布のパラメータではなくMLPのパラメータです。
なので、pθ(..)で表示すれば、確率変数名は何であれ、変数の分布は同じ構造のmanifoldになます。
逆に言えば、同じではない分布なら、皆pθ(..)で表示すべきではないと思いますね。
仮令Gaussian分布であっても、同じ分布ではない場合が多いのです。
なので、同じ処に異なる分布を全部pθ(..)で表すに困惑すると主張しました。
(この分野では論文の作者が時々省略するためにそういうふう書かれる場合が多いかと思います)
＊＊＊＊＊zuka 様の場合：
pθ(..)や qΩ(..)がMLPそのものだと思っていらっしゃませんか。
もしそうであれば、賛同できませんね。
ーーーーーーーーーーーーーーー
MLPは確かに最終的にP(..)で表現している変数空間の分布を再構成してくれますが、MLPの構造とパラメータとP(..)のそれとまったく別物であることに我々の認識は一致しているのでしょうか。
またご意見宜しくお願い致します。
前回の議論を踏まえて
pθ(x|z),pθ(z),pθ(x)を同じ処で現れるのはまずいと思われる理由：
分布・確率の関数名同じに上、見かけ上のパラメーθも同じですね。誰が見ても同じ分布であると思いがちです。
ところが、pθ(z)は事前分布としてN(0,I)に仮定さており、pθ(x)はdecoderとしてのMLPにより再構成しようとしているもので、pθ(x|z)はxに関する条件分布であり、三者は概念的にまったく異なるものですね。
仮令、同じGaussian類の分布であっても、同じ分布と限らないのです。ましてやサンプルデータの空間分布がGaussianに仮定できないでしょう。
Decoderのパラメータθがzの分布に影響を与えるのはやはり原理的に不可能ですね。
原論文《Auto-EncodingVariationalBayes (P.Kingma )》自身もzの分布を直にN(0,I)設定しております。
zの分布をも学習で決めたいなら、Decoderではなく、もう一つのNNを追加しなければなりません。
これに関して、例えば、論文に紹介されています。
即ちEncoderとDecoder以外にもう一つのNNに対する訓練を行います。
『Thus, CVAE uses three trainable neural networks, while VAE only uses two.』(P3)
よって、論文《Auto-EncodingVariationalBayes (P.Kingma )》Figure1の表現の仕方やPθ(z)のような書き方は問題です。
ちなみに、(Ivanov ICLR 2019)の論文の中に分布関数の書き方に結構注意されているので、なんとなく納得感あります。
教科書的にp(x|z)とp(x)が併存しますが、
具体技術分野においてやはりpθ(x|z)とpθ(x)pθ(ｚ)のような表現が同時に存在するのは避けたいですね。全然違う分布ですから。
をつけると表示しない現象ありますので
「これに関して、例えば、論文に紹介されています。」：
これに関して、例えば、論文《VARIATIONAL AUTOENCODER WITH ARBITRARY CONDITIONING(Ivanov ICLR 2019)》に紹介されています。
★★ごめんなさい！
いつも肝心な処が忘れています：
zuka様が強調されたようにDecoderが再構成のデータを生成するのではなく、分布のパラメータμθとσθを生成するだけですね。そうしますと、再構成のデータがどうやって生成されたのでしょうか。例えば、μθとσθで解析に決められたのでしょうか。
ご質問ありがとうございます。
質問1：$p_{\theta}(.)$は全て同じ構造を表しているのか
確率変数によって表す分布は異なります。ネットワークのパラメータ$\theta$，$\phi$を利用するという状況下で，対象とする確率変数を変えれば表される分布も変わるような「上手い」パラメータを学習するのがキモです。
質問2：$p_{\theta}(.)$や$q_{\phi}(.)$はNN（ニューラルネットワーク）を表しているか
$p_{\theta}(.)$と$q_{\phi}(.)$は確率分布ですので，ニューラルネットワークとはそもそもの概念としての出発点が異なります。しかし，NNを入力-出力機構として捉えた場合に，ニューラルネットワークの入力と出力に様々な確率分布を仮定することができます。逆に，入力と出力に様々な確率分布を仮定することでニューラルネットワークを学習させることも可能になります。確率的にNNを発展させることにより，ベイズ推論のような議論も可能になります。
質問3：$p_{\theta}(.)$に関する分布を全て$p_{\theta}(.)$で表すのは分かりにくいのではないか
これはやはり，全て$p_{\theta}(.)$として表すことに意味があると私は思います。なぜなら，1つのエンコーダ・デコーダでVAEは構成されているからです。これが複数のエンコーダ・デコーダに拡張されれば，$r_{\omega}(.)$などと表記することになると思います。
質問4：やはりデコーダ側のNNのパラメータ$\theta$が$z$に影響を与えるのは不可能なのではないか
デコーダは$z$を入力として学習していきますので，入力の良さもデコーダのパラメータに影響を与えます。つまり，デコーダのパラメータ更新を行う中で$z$も対応して更新されていきます。
質問5：再構成データはどのようにして生成されるのか
本文中にあるVAEの図の1枚目のようにパラメータを出力する場合はサンプリングなどを利用します。これは，ネットワークの末端ですので誤差逆伝播には影響を与えません。2枚目のように再構成データそのものを出力する場合はデコーダの出力そのものが再構成データになります。
丁寧なご解説よく分かりました！
本当に大感謝です。
それに数式(3)~(15)は原論文より分かりやすく、素晴らしかったのです！
特に式(12)と(15)が面白いと思います。
それによりますと、もし訓練過程によってL(x;φ,θ)を最大化にすれば、両式中のDKL部分が皆0になり、即ち、qφ(z|x)= pθ(z|x); qφ(z|x)= pθ(z)になります。これでさらにqφ(x)= pθ(x)が導かられる。
これはまさに理論上の目的(理想状態)ですよね。
★Q1: 果たして、訓練過程でL(x;φ,θ)を最大化にするのでしょうか。
★Q2: VAEの図の1枚目のようにパラメータを出力する場合はμθとσθしか生成されないのに、どうやって再構成データを得られるのでしょうか。もう少し詳してご説明お願いできますか(前回のご説明が理解できなかったのです)
大変申し訳ございませんが、また宜しくお願い致します。
ごめんなさい、一部自問自答をさせてください。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
“変分下限” , “ELBO”, 『reparametrization trick』
L(x,z) は 変分下限 (variational lower bound) または ELBO (evidence lower bound) と呼ばれます。
VAEではL(x,z) を目的関数としています。
★ VAEの学習では, 目的関数L(x,z)を【最大化】するようにパラメータθ,ϕ を選びます。
zに関して生成関数がなければ、バラバラのデータになってしまい(「ギブスサンプリング」で生成した場合も同じ)、即ちzをサンプリングする操作であれば微分不可能になり,
それより前のEncoder側に勾配を伝える(逆伝搬する)ことができなくなります。そのために、
『reparametrization trick』という方法で、
zの生成を下記のように関数化して微分可能になります。
z =μ(x) + ε⦿∑(x)
ε~N( 0, I)
これで逆伝播(Backpro…)が実現可能！！
前文の補足：
VAEではELBOを最小化にするか、それとも最大化にするかはELBOの定義によりますね。
本文式(15)の場合は『最大化』で、式(15)に(-1)掛けた場合は『最小化』になります。
あっ、そうだですね。悟った！
pθ(z)は予めN(0,I)に設定されていますけれども、
これはdecoder(θ)からencoder(Φ)へのフィードバック(backpro…)によって実現されたと考えられます。
即ち式(15)から分かるようにL(x,z)の最大化でqφ(z|x)= pθ(z)になるはずです。
なので、zの分布は結局decoder(θ)からencoderのφに影響してqφ(z|x)= p(z)(= N(0,I))にさせるため、
p(z)をpθ(z)で表示するわけですね。
ただ、p(z)そのまま表示される文献が多いようです。
あっ、悟りました！
pθ(z)は予めN(0,I)に設定されていますけれども、これはあくまでqφ(z|x)の目標値であって
decoder(θ)からencoder(Φ)へのフィードバック(backpro…)によって実現されると考えられます。
即ち式(15)から分かるようにL(x,z)の最大化【注】でqφ(z|x)=pθ(z)になるはずです。
なので、zは結局decoder(θ)からencoderのφに影響して生成されて、その分布 p(z)(=N(0,I))= qφ(z|x) にさせるため、
p(z)をpθ(z)で表示するわけですね。
ただ、p(z)そのまま表示される文献が多いようです。
【注】
L(x,z)を『最大化』するかそれとも『最小化』するかはL(x,z)の定義によります。
本文式(15)のような定義式であれば、L(x,z)を最大化することで、
L(x,z) = (-1) × 式(15)
のような定義の仕方も見かけますので、この場合はL(x,z)を最大化に相当します。
あっ、悟りました！
pθ(z)は予めN(0,I)に設定されていますけれども、これはあくまでqφ(z|x)の目標値であって
decoder(θ)からencoder(Φ)へのフィードバック(backpro…)によって実現されると考えられます。
即ち式(15)から分かるようにL(x,z)の最大化【注】でqφ(z|x)=pθ(z)になるはずです。
なので、zは結局decoder(θ)からencoderのφに影響して生成されて、その分布 p(z)(=N(0,I))= qφ(z|x) にさせるため、
p(z)をpθ(z)で表示するわけですね。
ただ、p(z)そのまま表示される文献が多いようです。
【注】
L(x,z)を『最大化』するかそれとも『最小化』するかはL(x,z)の定義によります。
本文式(15)のような定義式であれば、L(x,z)を最大化することで、
L(x,z) = (-1) × 式(15)
のような定義の仕方も見かけますので、この場合はL(x,z)を最大化に相当します。
訂正↑
L(x,z) = (-1) × 式(15)場合は
L(x,z)を【最小化】に相当します。
訂正：
L(x,z) = (-1) × 式(15)
のような定義の仕方も見かけますので、この場合はL(x,z)を【最小化】に相当します。
↑訂正：
L(x,z) = (-1) × 式(15)
のような定義の仕方も見かけますので、この場合はL(x,z)を【最小化】に相当します。
このプラットフォームの欠点：
１．編集・修正できない
２．削除・撤去できない
３．表示が時間ラグでかい
どこが経営してるのでしょうか。
何時も『あなたのコメントは管理者の承認待ちです』？
少し立て込んでおり，返信が遅れてしまいました。失礼致しました。
質問1：訓練課程で$L(x; \varphi, \theta)$を最大にするのか
その通りです。
質問2：再構成データはどのようにして生成されるか
分布のパラメータが分かれば，統計量を元にデータを再構成することができます。例えば，データの代表点として平均値を取るようにする，毎回ランダムサンプリングする，などです。分布から標本値を取っていくことで，データを再構成していきます。
質問3：$q_{\phi}(z|x)=p_{\theta}(z)$となるように学習されているのか
完全なイコールにはなりません。なぜなら，VAEの目的関数には$E_{q_\varphi (z|x)}[\log p_\theta (x|z)]$が含まれているからです。KLダイバージェンス側が0になるとは限りません。再構成誤差とKLダイバージェンスのバランスを見ながらネットワークは学習されていきます。
質問4：コメントプラットフォームに関して
こちらは「JIN」というワードプレス用テンプレートを利用しています。ご指摘の内容を，運営チームに報告してみます。
明けましておめでとう御座います！
御返答ありがとうございました。
自分の経験からしますと、Encoderの出力が『平均ベクトル』と『分散共分散行列』である事はVAE原理の理解のための一番高いハードルになっています。
今も理解できていません。
Encoderの出力をどうして『平均ベクトル』と『分散共分散行列』と解釈されるの？とご説明いただければ非常に助かります。例えば、一体、誰の『平均ベクトル』と『分散共分散行列』でありますか？ 訓練サンプルのでしょうか。
しかしEncoderの形成と訓練サンプルの『平均ベクトル』と『分散共分散行列』の計算とは数学上の関連性がまったくありません。もっと言えば、どんな分布の訓練サンプルセットであっても、NNの訓練による生成したdata mapping(射影)機構としてのEncoderの出力μと∑が0のvectorと1のvectorにする事が可能です。
これについて、議論していただきたいです。
【次は上の２つの図に関する異議】
ここでいう『平均ベクトル』と『分散共分散行列』は怪しい！ 誰の『平均ベクトル』と『分散共分散行列』？
入力data(vector)の？『平均ベクトル』と『分散共分散行列』を統計計算して得たのでもなければ、
原理的に、Encoderがどんな入力に対しても必ず『0』vectorと『1』vectorが
上のVAEの構造図(１枚目と2枚目)の中に、
εがまるでEncoderより生成されたようですが、
これは非常に誤解されやすいのですね。
実際、εは決してEncoderとは関係していません。
εはN(0,1)分布に従う確率変数値として直接ランダム関数から得たのです。
【よく勘違いされるのですが，VAEは「確率分布のパラメータ」を出力しているのであって，値そのものを出力しているわけではありません。】
これに非常に理解し難いです。
もともとencode-decodeというのは信号の圧縮と復元のためであって、もしそうでなければ、
最終的に平均値μθとσθを生成するのであれば(１枚目の図)、意味がないのでは？ そして、
第一に、μθとσθは集団的な統計量であって、特定の入力と一対一対応関係がないため、入力を復元できません。
第二に、もし出力が入力と同じタイプの量であれば(２枚目の図)、両者間の誤差を取り、学習できるのですが、
もし入力が画像データで、出力はμθとσθであれば、
どうやって学習するのでしょうか。
外部リンク<>の実装コードも
問題あります：
forward(self, x)の中にすでに
mean, var = self._encoder(x)
z = self._sample_z(mean, var)
x = self._decoder(z)
を実行しているのに、
def loss(self, x)の中にもう一度同じコールをやっています。
mean, var = self._encoder(x)
z = self._sample_z(mean, var)
y = self._decoder(z)
そうであれば、 forward(self, x)の存在意味が無くなりますよね？！
書いたものが一旦表示され、再度確認しようとしたら消えちゃった！！！ (数回遭遇)
実装コードに問題あると指摘したかったが、消えてしましました。
数日後また現れるような現象もあったような感じです。
不思議な此処
実装コードに問題あります：
forward(self, x)の中にすでに
mean, var = self._encoder(x)
z = self._sample_z(mean, var)
x = self._decoder(z)
を実行しているのに、
loss(self, x)の中にもう一度同じコールをやっています。
mean, var = self._encoder(x)
z = self._sample_z(mean, var)
y = self._decoder(z)
そうであれば、 forward(self, x)の存在意味が無くなりますよね？！
あけましておめでとうございます。
ご質問ありがとうございます。
１．Encoderの出力が『平均ベクトル』と『分散共分散行列』である事について
Encoderの出力は潜在空間のパラメータです。すなわち，「誰の」に対する回答は潜在空間ということになります。訓練データの統計的な性質を表しているわけではありません。
２．画像中の$\epsilon$の生成に関して
ご指摘ありがとうございます。修正いたしました。
３．VAEの学習原理に関して
出力がパラメータである場合，式(16)のように分布を仮定して解析的に更新式を求めていきます。
４．実装コードに関して
ご指摘ありがとうございます。たしかに，loss関数をforwardを使って書けますね。ただ，今回は効率的な実装コードというより，VAEの動作機構を明確に細かく示したいというモチベーションがあるため，一旦このままにさせてもらいます。
５．コメント欄の誤動作に関して
こちらは私の方では対応できかねる問題になります…。一応要望を出してはいるのですが，なかなか実現していただけないのが現状です。
お返事有難うございます！
この前書いたと思いましたが、消えているみたいで、
改めて出します。
_encoder関数の中にzのvariance value(var)を生成するためにsoftplus(..)関数を利用されるのは疑問ですね。
１．これで事実上、本来関連性のないvariance element同士に人為的に関連付けられ、不必要に制限されてしまいます。
２．とりわけまずいのはsoftplus(..)関数は計算対象同士の中の大きい値を猛烈に拡大して、小さい値を一層小さくする働きがあって、zのvariance valueに対して意味のない改造が行われてしまいます。
３．通常softplus(..)を利用せず、log(var)の形でencoderの出力としているらしいです。
これはメリットがあると思います。
なぜなら、1以下の値のセットの分散も1以下であるので、logの場合は1以下の値の微小変動に敏感に反応(拡大)し、学習収束の能率に貢献できると思われますね。
＝＝＝＝＝＝＝＝＝＝＝＝
上記１～３はまったく個人見解で、正しい保証もないので、議論したいだけです。
【続】ただし、 _decoder関数の中でsigmoid関数を利用して、画素値の復元を行うのは適切だと思います。∵ ここでは画素値を[0,1]に限定されているので、画像も一種の確率分布に見立てられます。
( だから、入出力画像間の距離を分布の距離測度 cross entropy や Kullback–Leibler divergenceで測ります。)
ご質問ありがとうございます。
1. encoder中のsoftplusに関して
こちらのexampleにもある通り，エンコーダの出力は$\log \sigma^2$とする場合が多いようですね。その際は，fc層の出力をそのまま利用してOKです。ただし，私の実装はfc層で$\sigma^2$を出すようにしていますので，非負値であるという制限が必要になります。微分可能で非負値を出力する関数としてsoftpusを利用していました。softplusによって$\sigma^2$の要素が独立でなくなるということですが，fc層を通している時点でもはや独立ではないと考えられます。実装を少し変えてみますので，ご確認ください。
先送ったcommentがまたも消えた？？？
こちらでは確認できておりません。
お手数ですが再度送信いただけますでしょうか。
見事に消えましたね。—–でも数日後にまた現れるかもしれません。
内容としてお詫びです。
この前＜softplus(..)関数を利用されるのは疑問ですね＞に関する議論1.,2.は、SoftMax(..)関数の話であるべきで、softplus(..)関数に関する話ではありあせん。
ただ、softplus(..)関数は逆に小さい数値ほど拡大される癖があるので、依然、この前のように数値σやμのregressionに利用されるのは適切かに疑問です。
例えば、Encoderが生成したμの値が0になってもsoftplus(..)を経由したら0より大きくなるので、0に近いμを得るには遅くなるかな。。。
なにはともあれ、論文から実装できるのは素晴らしいですね！頑張ってください！
訂正：
誤：
《softplus(..)関数は逆に小さい数値ほど拡大される癖があるので》
正：
softplus(..)関数は逆に正の小さい数値ほど拡大される癖があるので
ご時間あれば、是非IntroVAEの実装と効果評価のようなトピックを建てていただきたいですね。
その次はSNIPや「Cascade R-CNN」かな。。。
(実験付きの議論があれば一層ありがたいと思います。)
ご提案ありがとうございます。
sigmoid云々に関する話題から，自分の実装を見直す良い機会になりました。
単に非負値を防ぐというためだけに脳死でsoftmaxなどを利用するのは好ましくないですね。
最新の手法の再現実装も頑張りたいと思います。
こんにちは。
コピペで動きそうだったので試したのですが「生成」のところの以下のコードでひっかかり
y, z = model(x)
試しに
loss,z,y = model(x, device)
に変更して動かしましたが、出てくる画像は0と8の混ざったような画像だけでした。
hoge様
ご連絡ありがとうございます。
modelを呼び出すところのコードですが，もしかすると修正前の古いバージョンのキャッシュが残ってしまっている可能性があります。
恐れ入りますが，ブラウザのキャッシュを削除した後に，もう一度弊サイトのコードをご覧いただけますでしょうか。
また，出てくる画像が中途半端なぼやけた画像になってしまうのは，こちらのミスでして，現在原因究明中です。（お問い合わせより同内容のご連絡をいただいており，本文中にその旨を追記しています。おそらくキャッシュを削除すれば見えるようになるかもです。）
考えられる原因としては，だいぶ前にちょこっとコードを修正した際にどこかがバグったものと思われます。
もしまた何かご指摘いただけましたら幸いです。
zuka
zukaさん
ありがとうございます。その後、試行錯誤してうまく動きました！
これからじっくり解読していきます
hoge様
ご連絡ありがとうございます。
本記事の内容も未熟だと思いますので，ぜひまたご指摘ください。
恐れ入りますが，どこを改善したらうまく動くようになったか，覚えている範囲で教えていただけますと助かります><
はじめまして！
本記事、大変参考にさせていただいております。
今、Excelに格納されたモーションデータを教師データとしてモーションの生成を行いたいと考えております。
そこでVAEかCVAEを用いた方がいいのではという意見が上がりました。
zukaさんでしたらどちらを使用するのが良いと思いますでしょうか？
もし可能でしたらVAEとCVAEの違いについても確認のためご説明いただけましたら幸いです。
よろしくお願いい致します。
ただの大学生様
ご連絡ありがとうございます。
また，返信が遅れてしまい，大変申し訳ございません>< CVAEを簡単に説明するとすれば，ラベルを付与したVAEです。「Conditional」がラベルというような意味合いです。 モーションデータの形式や内容を確認しないと何とも言えないのですが，どのようなデータなのかを簡単に教えていただけますでしょうか。
はじめまして。
ＶＡＥを調べていて辿り着きました。丁寧な解説文ありがとうございます。
現状のサンプルコードで生成画像がぼやけてしまう現象ですが、
reconstrunctionのクロスエントロピ損失計算にmeanではなくsumを
使う事で解決しました。
# reconstruction = torch.mean(x * torch.log…
reconstruction = torch.sum(x * torch.log…
meanだと、何にでも見えるぼやけた画像で再生成誤差の損失が停滞してしまう
ので、この場合は１つでも間違っている間は大きなペナルティが課される
sumの方が良いかな、と思いました。
損失値が大きくなって、学習カーブが例と違うのでzukaさんの意図と異なる
かも知れませんが参考になればと思います。
Zukaさん
もう少し調べました。sumとmeanの違いというより、KLとクロスエントロピーの比率の影響のようでした。すみません。損失計算からKL項を外してやるとmeanでも正しく画像を生成できました。各々のロスのログを取ってやると、meanの場合はKLとクロスエントロピーが近い値で始まり、KLの方が速く減っていきます。潜在変数を正規分布にする事を優先する余り、全ての画像に対する潜在変数を中央に寄せてしまい、結果的に全ての数字の画像の平均をとったようなボヤけた画像になって、そこから抜け出せなくなるのでは、と推測しています。ラベル別に潜在変数の分布をグラフ表示すると、見事に中央にごちゃ混ぜになってました。
通りすがりの初心者様
コメントありがとうございます！
こちらのミスで，コメント通知がOFFになっており，ご返信が遅れてしまったことをお詫びいたします。
後ほど返信差し上げます。
通りすがりの初心者様
大変有益な情報提供をありがとうございます！！
VAEではKLとクロスエントロピーの重みを変えていく（最初は再構成誤差強め）ことはよく行うのですが，盲点でした泣
読者の皆様の参考にさせていただきたく思いますので，本文で引用させていただきます。
助かりました。
通りすがりの初心者様
追記です。
再構成誤差の項ですが，モンテカルロ近似を1つのサンプルで行っているため，meanではなく本来sumが正解です。meanを取ってしまうとバッチ方向まで余分に均してしまうために，再構成誤差の項がKLと比べて相対的に小さくなってしまい，posterior colappseが起きて事後分布が事前分布に一致してしまい，ぼやけた画像が生成されていたようです。恥ずかしながら，今になって気付きました。
zuka様 わかりやすい記事を有難うございます
VAEおよびpythonについて勉強を始めてこちらのアンプルコードを実行させていただきました。
ですが、学習部分でエラーを吐いてしまい、実行ができませんでした。
よろしければ、このコードを実行したときのpythonのバージョンを教えていただけないでしょうか。
python初学者さま
ご質問ありがとうございます。
本記事の内容は，より洗練させて以下の記事に移植済みでございます。
https://academ-aid.com/ml/vae
恐れ入りますが，上記記事をご参照の上，それでもコードが動かなければ上記記事のコメント欄にて再度お申し付けください。なお，実装自体は以下のGithubリポジトリに格納してあります。よろしくお願い致します
https://github.com/beginaid/VAE