本記事の内容は新ブログに移行されました。
こちらのブログにコメントをいただいても
ご返信が遅れてしまう場合がございます。
予めご了承ください。
ご質問やフィードバックは
上記サイトへお願い致します。
今回は,確率モデルの潜在変数・パラメータの事後分布を求めるための繰り返し近似法である変分ベイズ法(Variational Bayesian methods)の解説とPythonで実装する方法をお伝えしていこうと思います。
本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。また,本記事の実装はPRML「パターン認識と機械学習<第10章>」に基づいています。演習問題は当サイトにて簡単に解答を載せていますので,参考にしていただければと思います。

VBの気持ち
機械学習を学ばれている方であれば,VB(変分ベイズ)の意味分からなさ加減にはウンザリしたことがあると思います。私自身,学部時代にPRML(機械学習のバイブル的書籍)をパラっと見たとき,あまりの難しさから途方にくれてしまったのを覚えています。VB(変分ベイズ)では何をしたいのか,そもそも何のための手法なのかが見えなくなってしまう場合が多いと思いのではないでしょうか。
そこで,今回は実装の前に,簡単にVBの気持ちをお伝えしてから,ザッと数学的な背景をおさらいして,最後に実装を載せていきたいと思います。早速ですが,一問一答形式で変分ベイズ法に関してみていきたいと思います。
疑問1:何のための手法なの?
 現象を確率モデルで説明
現象を確率モデルで説明VBは確率モデルの潜在変数・パラメータに関する事後確率を計算するための手法です。噛み砕いていきましょう。確率モデルというのは,簡単に言えば「現象の裏側に何か適当な分布を仮定すること」です。
分布を仮定するというのは,尤度関数を定めることに相当します。ほとんどのタスクでは,私たちの目標は事後分布を求めることです。ベイズの定理より,尤度関数と事前分布をかけ合わせると事後確率になります。(詳しくは「【初学者向き】ベイズ推論とは?事前分布や事後分布をド素人向けに分かりやすく解説してみます!」へ)
ですので,尤度関数を仮定したところで,事前分布を定められなければ事後分布を手に入れることができないのです。そして,変分ベイズの本領が発揮されるのは,モデルの事前分布を定められないときです。
多くのベイズモデリングでは,事前分布に共役事前分布を仮定しますが,変分ベイズ法では共役事前分布を持たない,もしくは部分的な共役性をもつ確率モデルの推論を対象とします。
疑問2:EMアルゴリズムとの違いは?
 EMアルゴリズムのMステップ
EMアルゴリズムのMステップEMアルゴリズムや変分ベイズでは,対象とする現象に確率モデルを仮定しましたね。しかし,適当な分布を仮定したところで,その分布の形状を決定するパラメータを定めなくては,現象を確率モデルで説明することはできません。そこで,得られた情報(現象)に尤も良くフィットするようなパラメータを求める操作が「最尤推定」でした。そのための手法がEMアルゴリズムでした。(→【かゆい所に手が届く】EMアルゴリズム解説とPythonによるGMM(混合ガウス分布)への実装。)
しかし,最尤推定にはいくつかの欠点があります。まず,前提の認識として,最尤推定は「点推定」に相当します。求めたいパラメータを「1つの値」に決めつけてしまう手法です。たとえば,EMアルゴリズムでは最尤解を計算しますが,平均は3.2,分散は1.3などといったように,具体的な数値で結果が出てきます。
これらは,高校まで習ってきた数学の問題によく似ています。「関数$f(x)$を最大にする$x$の値を求めなさい」という問題では,$x$の値を微分か何かを利用して求めていましたね。正確性は欠けますが,これが点推定に相当します。
しかし,例えばモデル化する対象が「多峰性」の分布である場合,どうでしょうか。多峰性というのは,多くのピークを持つ性質のことを指します。この場合,点推定では片方のピークの情報を完全に捨ててしまうことになります。他にも,真の分布がなだらかな場合,点推定をしてしまうと偏った推定結果を導くことになってしまいます。(過学習)
もっと,こう,曖昧さを表現できる推定方法はないのでしょうか。たとえば,$f(x)$が複数のピークを持つときに,
みたいな推定ができれば嬉しくないでしょうか。ここで登場するのが,ベイズ推論です。尤度関数を最大にするパラメータを求めるのが「最尤推定」でした。一方,ベイズ推論では,パラメータに確率分布を仮定してしまいます。ここが,変分ベイズを考える際の出発点となります。確率分布を仮定することで,曖昧さを表現できるようになるのです。
つまり,EMアルゴリズムは最尤解を点推定するための手法,変分ベイズは事後確率をベイズ推定するための手法だと言えます。
疑問3:変分ってどういう意味?
 超おおざっぱな理解
超おおざっぱな理解変分ベイズの「変分」は,変分法が由来となっています。変分法というのは,超噛み砕いて言えば,微分の変数が関数になった処理のことを指します。高校の微積分では,変数は基本的に実数でした。大学の微積分では,まずは複数の変数についての処理を学び(偏微分・重積分),その次にベクトルや行列に関する処理を学びます。さらに進むと,変数が関数になったバージョンを学ぶことになります(変分法)。
その通りです。変分ベイズでは,求めたい事後分布をある関数で近似します。変分ベイズは,このような操作をベイズ推論の枠組みで行うことから,「変分」「ベイズ」と呼ばれているのです。
疑問4:メリットは?
上でもお伝えした通り,曖昧さを表現できるのが変分ベイズのメリットです。他にも,クラスタリングのタスクを例に考えたとき,EMアルゴリズムではクラスタ数は自分で設定しなくてはなりませんでした。
一方,変分ベイズでは,初期値は自分で設定するのですが,多少大きめの値を設定しておくことで,不要な要素が0に近づいてくれるという性質があります。このように,スパースな結果を学習してくれる機能は,関連度自動決定と呼ばれています。
疑問5:デメリットは?
いいことばっかりの変分ベイズと思いがちですが,実は欠点もあります。まず第一に,多くの場合,更新式の導出が難しいという点が挙げられます。下でも説明しますが,なかなか骨の折れる計算が多いです。他にも,真の分布を近似する手法のため,サンプリング法と比べた場合に重要な情報が抜け落ちてしまう場合があります。
疑問6:なぜ近似だけで尤度が最適化されるの?
 手法Bの考え
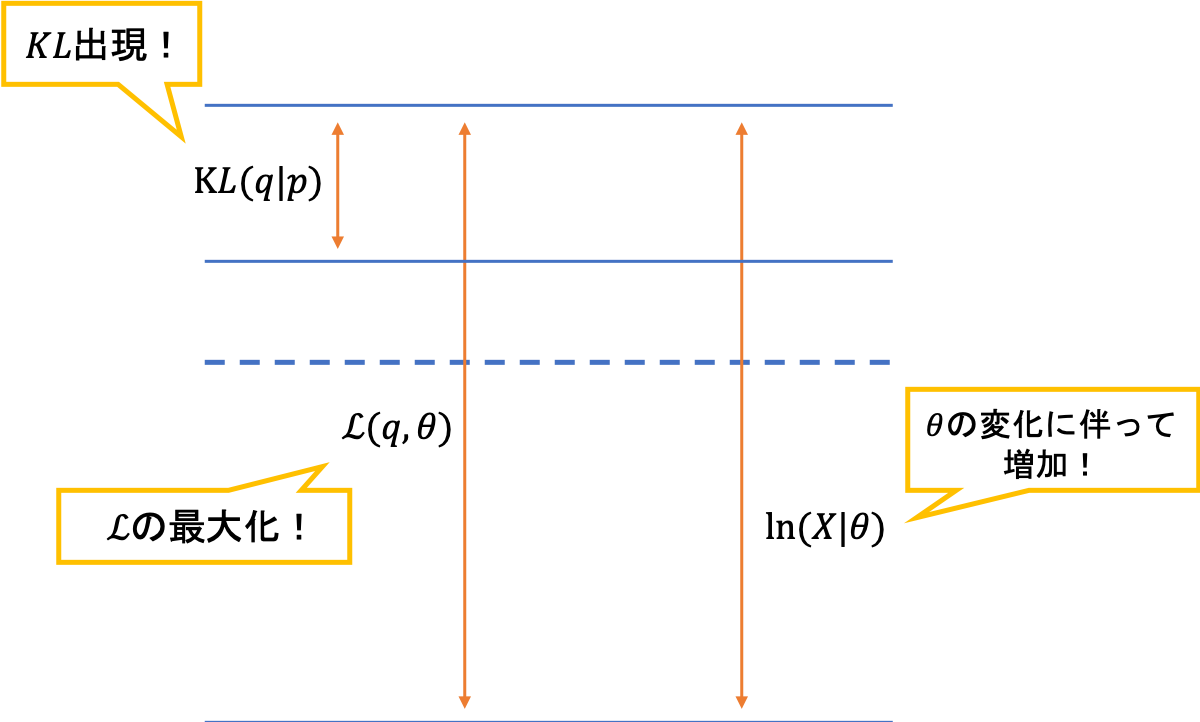
手法Bの考え非常にクリティカルな質問だと思います。EMアルゴリズムでは,Eステップでは尤度を一定に保った中でKLダイバージェンスを最小化する$q$を選びました。また,Mステップでは,下界を最大化することで,尤度を底上げしました。このステップの繰り返しで,尤度が徐々に最大化(最適化)されていくイメージはつきやすいと思います。
一方,変分ベイズでは,EステップでもMステップでも偏微分やラグランジュの未定乗数法等を利用した最適化手法は用いられません。しかし,それでも,尤度を計算すると増加していくのです。
この疑問に答えるカギは,EMアルゴリズムと変分推論の目的関数の違いです。EMアルゴリズムでは「対数尤度」が目的関数であり,二つの項に分解されました。
\begin{eqnarray}
\ln p(\boldsymbol{X}|\boldsymbol{\theta}) = \mathcal{L}(q, \boldsymbol{\theta}) + KL(q\|p) \notag
\end{eqnarray}
一方,変分推論では,対数モデルエビデンス$p(\boldsymbol{X})$を目的関数として,二つの項に分解します。
\begin{eqnarray}
\ln p(X) = \mathcal{L}(q) + KL(q\|p) \notag
\end{eqnarray}
対数尤度は,パラメータに依存するため,パラメータの更新によって値が変わります。EMアルゴリズムではMステップに相当します。一方,モデルエビデンスはパラメータに依存しないため,パラメータを更新したところで値は不変なのです。ここが変分ベイズを理解するための肝であり,多くの人が勘違いをしてしまうポイントになります。
つまり,変分推論では,与えられたデータをよく説明できるようなパラメータとなるように,毎回の更新を行なっているのです。その結果,対数尤度は増加していくことになります。
変分ベイズ
まずは変分ベイズの概要について確認していったうえで,後ほど混合ガウス分布の推論に適用していくという流れにしましょう。
変分ベイズの説明には,大きく分けて2通りの方法があります。1つ目は,事後分布とのKLダイバージェンスを最小化するような分布(制限付き)を求めてしまうという方法(手法A)です。「ある制限」は後ほど解説します。直感的には,こちらの方法の方が分かりやすいと思います。
【手法Aの思考】
●$p(\boldsymbol{Z} | \boldsymbol{X})$を求めたい
↓
●しかし計算が難しい
↓
●ある制限(※)下の分布$q(\boldsymbol{Z})$で近似しよう
↓
●距離尺度はKLダイバージェンスを使おう
↓
●$KL(q \| p)$を最小化する$q$を求める
もう1つの手法は,EMアルゴリズムと同じ枠組みで,尤度関数(周辺尤度)を下界とKLダイバージェンスの2つに分解して考えていく方法(手法B)です。発想は先ほどの手法Aと同じで,KLダイバージェンスを最小化するような$q$(制限付き)を求めることです。
\begin{eqnarray}
\ln p(X) = \mathcal{L}(q) + KL(q\|p)
\end{eqnarray}
下界とKLダイバージェンスの定義は,以下の通りです。
\mathcal{L}(q) &=& \sum_{\boldsymbol{Z}}q(\boldsymbol{Z})\ln \{ \frac{p(\boldsymbol{X}, \boldsymbol{Z})}{q(\boldsymbol{Z})} \} \\
KL(p | q) &=& – \sum_{\boldsymbol{Z}} q(\boldsymbol{Z}) \ln \{ \frac{p(\boldsymbol{Z} | \boldsymbol{X})}{q(\boldsymbol{Z})} \}
\end{eqnarray}
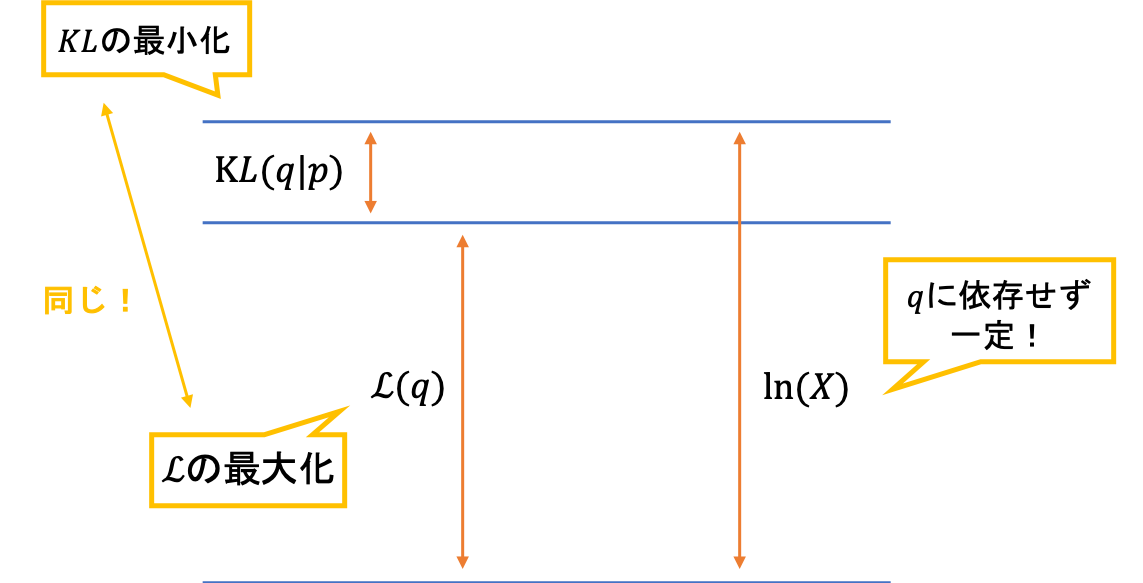
実は,先ほどのKLダイバージェンスと,尤度関数(周辺尤度)を分解して出てきたKLダイバージェンスは同じことが分かります。そして,$\ln p(X)$が$q$に依存しないことをふまえると,$q$に関してKLダイバージェンス$KL(q\|p)$を最小化することは,$q$に関して下界$\mathcal{L}(q)$を最大化することに相当します。手法Bでは,このようにしてKLダイバージェンスの問題を下界の問題に置き換えて考えていきます。
 手法Bの考え
手法Bの考えそうですね。手法Aを利用しないで,手法Bを考えるメリットはどこにあるのでしょうか。上で見たように,手法Aと手法Bは本質的に同じ操作を行なっています。ですので,数学的な背景も,下でお伝えするように,ほぼ同じです。
しかし,下界に注目して考えることで,最尤推定やMAP推定との関わりが一気に明らかになるのです(手法Aでもバラバラではありますが,明らかになります)。後ほど,数式で説明しますね。
【手法Bの思考】
●$p(\boldsymbol{Z} | \boldsymbol{X})$を求めたい
↓
●手法Aを使うか…?
↓
●数学的な背景を一貫させたい
↓
●EMと同じ分解を考えよう
↓
●下界$\mathcal{L}(q)$を最大化する$q$を求める
さて,上では説明を省いていた「ある制限」について補足を加えておきます。この制限は,変分ベイズにおいて,非常に重要な仮定の1つとなります。具体的には,「平均近似場」と呼ばれる近似手法を利用します。
\begin{eqnarray}
q(\boldsymbol{Z}) = \prod_{i=1}^{M}q_i(\boldsymbol{Z}_i)
\end{eqnarray}
この式の解釈としては,事後確率$p(\boldsymbol{Z}|\boldsymbol{X})$をよく近似する$q(\boldsymbol{Z})$は,独立な分布(因子)$q_i(\boldsymbol{Z}_i)$の積で表されるという仮定を表しています。
たとえば,潜在変数の中に$\mu$,$\Sigma$,$\pi$が含まれているとした場合,それらのパラメータそれぞれに独立な分布を仮定するという意味です。その際,パラメータはグループに分割されますので,例えば$\mu$と$\Sigma$をまとめてある分布を仮定することも可能です。
それでは,以下では2つの手法に基づきながら,変分ベイズの一般的な枠組みを説明していきたいと思います。
手法A
以下では,ある潜在変数orパラメータ($\boldsymbol{Z_i}$)の分布を計算していきたいと思います。計算が大変そうに見えますが,表記がややこしいだけで,行なっている操作は高校生でも分かります。
5行目から6行目の変形が一番難しいと思います。期待値をとる変数以外の対象はそのまま残る(例:$E_x[3]=3$)ことの類推で考えていけばOKです。(スクロールできます)
q(\boldsymbol{Z}_i)
&=& \arg \min_{q_i} KL[q(\boldsymbol{Z}) \| p(\boldsymbol{Z}|\boldsymbol{X})] \\
&=& \arg \min_{q_i} KL[q_i(\boldsymbol{Z_i}) \cdot q_{j\neq i}(\boldsymbol{Z}_{j\neq i})\| p(\boldsymbol{Z}|\boldsymbol{X})] \\
&=& \arg \min_{q_i} E_{q(\boldsymbol{Z})}[\ln \frac{q_i(\boldsymbol{Z_i}) \cdot q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}{p(\boldsymbol{Z}|\boldsymbol{X})}] \\
&=& \arg \min_{q_i} E_{q_i(\boldsymbol{Z_i})}[E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln \frac{q_i(\boldsymbol{Z_i}) \cdot q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}{p(\boldsymbol{Z}|\boldsymbol{X})}]] \\
&=& \arg \min_{q_i} E_{q_i(\boldsymbol{Z_i})}[E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln q_i(\boldsymbol{Z_i})] + E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[ \ln q_{j\neq i}(\boldsymbol{Z}_{j\neq i})] – E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln p(\boldsymbol{Z}|\boldsymbol{X})]] \\
&=& \arg \min_{q_i} E_{q_i(\boldsymbol{Z_i})}[ \ln q_{i}(\boldsymbol{Z}_{i}) – E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln p(\boldsymbol{Z}|\boldsymbol{X})]] \\
&=& \arg \min_{q_i} E_{q_i(\boldsymbol{Z_i})}[\ln \frac{q_{i}(\boldsymbol{Z}_{i})}{\exp\{E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln p(\boldsymbol{Z}|\boldsymbol{X})]] \}}] \\
&=& \arg \min_{q_i} E_{q_i(\boldsymbol{Z_i})}[\ln \frac{q_{i}(\boldsymbol{Z}_{i})}{\frac{\exp\{E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln p(\boldsymbol{Z}|\boldsymbol{X})]] \}}{C}} – \ln C] \\
&=& \arg \min_{q_i} KL(q_{i}(\boldsymbol{Z}_{i}) \| \frac{\exp\{E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln p(\boldsymbol{Z}|\boldsymbol{X})] \}}{C})\\
\end{eqnarray}
q_{i}(\boldsymbol{Z}_{i})&=& \frac{\exp\{E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln p(\boldsymbol{Z}|\boldsymbol{X})] \}}{C} \\
\ln q_i(\boldsymbol{Z}_i)
&=& E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln p(\boldsymbol{Z}|\boldsymbol{X})] + \rm{const} \\
&=& E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln \frac{p(\boldsymbol{Z}, \boldsymbol{X})}{p(\boldsymbol{X})}] + \rm{const} \\
&=& E_{q_{j\neq i}(\boldsymbol{Z}_{j\neq i})}[\ln p(\boldsymbol{Z}, \boldsymbol{X})] + \rm{const} \\
\end{eqnarray}
ようやく,得たい式が得られました。こちらの式が,変分ベイズでは大活躍します。
\ln q_i^\ast(\boldsymbol{Z}_i) = E_{j\neq i}[\ln p(\boldsymbol{X, Z})] + \rm{const}
\end{eqnarray}
解釈,というより,覚え方みたいな感覚としては「自分以外の潜在変数orパラメータで期待値をとる」と理解しておきましょう。
手法B
手法Bは,手法Aの目的関数を下界に変えるだけです。一点注意すべきなのは,手法Aでは最小化をしていましたが,手法Bでは最大化をするところです。そこで,手法Aの計算結果を利用するために,手法Bも「負の下限の最小化」と問題を置き換えてしまいましょう。こうすることで,先ほどの結果を流用できます。
負の下限は,定義から下のようになります。
\begin{eqnarray}
\mathcal{L}(q)
&=& – \int q(\boldsymbol{Z})\ln \frac{p(\boldsymbol{X}, \boldsymbol{Z})}{q(\boldsymbol{Z})} \rm{d}\boldsymbol{Z} \\
\end{eqnarray}
これ,よく見ると,先ほどのKLダイバージェンスとほぼ同じ形をしているんですね。
KL(q \| p) &=& – \int q(\boldsymbol{Z}) \ln \frac{p(\boldsymbol{Z} | \boldsymbol{X})}{q(\boldsymbol{Z})} \rm{d}\boldsymbol{Z}
\end{eqnarray}
つまり,先ほどの結果で$p(\boldsymbol{Z} | \boldsymbol{X})$のところを$p(\boldsymbol{X}, \boldsymbol{Z})$で置き換えればOKです。すると,最後のベイズの定理を利用したごちゃごちゃした変形をせずに,式(18)を得ることができます。
最尤推定・MAP推定との関わり
手法Aと手法B,いずれを利用しても最尤推定・MAP推定との関係性が見えてきます。思い出して欲しいのは,最尤推定とMAP推定は「点推定」であったということです。変分推論では「ベイズ推論」をしました。この三者について,簡単にまとめておきます。
【最尤推定】
\begin{eqnarray}
\theta_{ML} = \arg \max_{\theta}\{ p(x|\theta) \}
\end{eqnarray}
【MAP推定】
\theta_{MAP} = \arg \max_{\theta}\{ p(x|\theta)p(\theta) \}
\end{eqnarray}
【ベイズ推論】
\begin{eqnarray}
p(\theta | x) = \frac{p(x|\theta)p(\theta)}{p(x)}
\end{eqnarray}
どの手法とも,観測データ$x$に最もフィットするパラメータを求めるという目的は一貫しています。最尤推定では,尤度を最大にするパラメータを点推定します。EMアルゴリズムは最尤推定を近似的に行う手法でした。
MAP推定では,尤度関数に事前分布の情報を付け加える(=事後確率)ことによって,より汎化性能のある点推定を実現しようとしています。事前分布をかけあわせることは,正則化の役割を果たしています。
ベイズ推論では,単にパラメータの事後分布を求めます。ここで,ベイズ推論だけ「推論」という言葉が利用されていることに気づきましたか?最尤「推定」やMAP「推定」は,何かしらの最適化手法(EMアルゴリズム等)を利用して尤もらしいパラメータの値を求めるのでした。
一方,ベイズ「推論」では,最適化手法等は用いていないことに注意が必要です。パラメータの値を求めるのではなく,パラメータの分布を求めているのです。(そのためには結局パラメータの分布を定めるパラメータを推定しなくてはならず,堂々巡りですが)
さて,以下では最尤推定とMAP推定が変分ベイズの特殊な場合に相当することを示していきたいと思います。基本的な方針としては,ベイズ推論において,事後分布を無限に尖った分布(クロネッカーのデルタ関数)と仮定することで点推定(MAP推定)と捉えることができます。加えて,事前分布が無情報(平坦な分布)である場合,MAP推定は最尤推定と捉えることができます。
手法A
変分推論にて,事後分布を近似するために用意する分布$q(\boldsymbol{Z})$をクロネッカーのデルタ関数$\delta({\boldsymbol{Z}-\hat{\boldsymbol{Z}}})$と仮定します。このとき,手法Aでは事後分布とのKLダイバージェンスを最小化するような$\delta({\boldsymbol{Z}-\hat{\boldsymbol{Z}}})$を求めるのでした。
先ほどの結果を利用するのではなく,もう少し一般的な話をしたいと思います。ですから,KLダイバージェンスの定義から数式を変形してみます。
KL(\delta(\boldsymbol{Z} – \hat{\boldsymbol{Z}}) \| p(\boldsymbol{Z}|\boldsymbol{X}))
&=& \int \delta(\boldsymbol{Z} – \hat{\boldsymbol{Z}}) \ln \frac{\delta(\boldsymbol{Z} – \hat{\boldsymbol{Z}})}{p(\boldsymbol{Z}|\boldsymbol{X})} \rm{d}\boldsymbol{Z} \\
&=& \int \delta(\boldsymbol{Z} – \hat{\boldsymbol{Z}}) \ln \delta(\boldsymbol{Z} – \hat{\boldsymbol{Z}}) \rm{d}\boldsymbol{Z} \notag \\
&& – \int \delta(\boldsymbol{Z} – \hat{\boldsymbol{Z}}) \ln p(\boldsymbol{Z}|\boldsymbol{X}) \rm{d}\boldsymbol{Z} \\
&=& \ln \delta(\boldsymbol{Z} – \hat{\boldsymbol{Z}}) – \ln p(\hat{\boldsymbol{Z}}|\boldsymbol{X}) \\
&=& \ln \delta(\hat{\boldsymbol{Z}} – \hat{\boldsymbol{Z}}) – \ln \frac{p(\boldsymbol{X} | \hat{\boldsymbol{Z}})p(\hat{\boldsymbol{Z})}}{p(\boldsymbol{X})} \\
&=& \ln \delta(\hat{\boldsymbol{Z}} – \hat{\boldsymbol{Z}}) – \ln p(\boldsymbol{X} | \hat{\boldsymbol{Z}}) – \ln p(\hat{\boldsymbol{Z}}) + \ln p(\boldsymbol{X}) \\
&\overset{\hat{\boldsymbol{Z}}}{=}& -\ln p(\boldsymbol{X} | \hat{\boldsymbol{Z}}) p(\hat{\boldsymbol{Z}})
\end{eqnarray}
式(25)から式(26)はクロネッカーのデルタ関数の性質を利用しています。
\begin{eqnarray}
\int \delta(\theta – \hat{\theta}) f(\theta) \rm{d}\theta = f(\hat{\theta})
\end{eqnarray}
つまり,KLダイバージェンスを最小化する潜在変数・パラメータは以下の式で表現されます。
\begin{eqnarray}
\hat{\boldsymbol{Z}}
&=& \arg \min_{\hat{\boldsymbol{Z}}} \{ -\ln p(\boldsymbol{X} | \hat{\boldsymbol{Z}}) p(\hat{\boldsymbol{Z})} \} \\
&=& \arg \max_{\hat{\boldsymbol{Z}}} \{\ln p(\boldsymbol{X} | \hat{\boldsymbol{Z}}) p(\hat{\boldsymbol{Z})} \}
\end{eqnarray}
どうでしょうか。見事MAP推定の式が出てきましたね。ちなみに,$\delta(\hat{\boldsymbol{Z}} – \hat{\boldsymbol{Z}})=\delta(\boldsymbol{0})$は無限大の値をとりますが,潜在変数・パラメータ$\boldsymbol{Z}$に依存しないために除外しました。
上の式で,潜在変数・パラメータ$\boldsymbol{Z}$の事前分布$p(\boldsymbol{Z})$が無情報(平坦な分布)だと仮定すると,MAP推定は最尤推定になるのでした。
\begin{eqnarray}
\hat{\boldsymbol{Z}}
&=&
\arg \max_{\hat{\boldsymbol{Z}}} \{\ln p(\boldsymbol{X} | \hat{\boldsymbol{Z}}) p(\hat{\boldsymbol{Z}}) \}\\
&=& \arg \max_{\hat{\boldsymbol{Z}}} \{\ln p(\boldsymbol{X} | \hat{\boldsymbol{Z}}) \cdot C) \}\\
&=& \arg \max_{\hat{\boldsymbol{Z}}} \{\ln p(\boldsymbol{X} | \hat{\boldsymbol{Z}}) \}
\end{eqnarray}
たしかに,尤度関数だけになることが確認できましたね。
手法B
同様のことを手法Bで確認していきます。上でもお伝えしたように,手法Bを考えるメリットは,変分推論と最尤推定・MAP推定の関係を同時に捉えられる点にあります。下界の定義をさらに変形して,KLダイバージェンスを出現させてみましょう。
\mathcal{L}(q)
&=& \int q(\boldsymbol{Z})\ln \frac{p(\boldsymbol{X}, \boldsymbol{Z})}{q(\boldsymbol{Z})} \rm{d}\boldsymbol{Z}\\
&=& \int q(\boldsymbol{Z})\ln \frac{p(\boldsymbol{X}| \boldsymbol{Z}) p(\boldsymbol{Z})}{q(\boldsymbol{Z})} \rm{d} \boldsymbol{Z}\\
&=& \int q(\boldsymbol{Z})\ln p(\boldsymbol{X}| \boldsymbol{Z}) \rm{d} \boldsymbol{Z} – \int q(\boldsymbol{Z})\ln \frac{q(\boldsymbol{Z})}{p(\boldsymbol{Z})} \rm{d} \boldsymbol{Z} \\
&=& \int q(\boldsymbol{Z})\ln p(\boldsymbol{X}| \boldsymbol{Z}) \rm{d} \boldsymbol{Z} – KL(q \| p)
\end{eqnarray}
ここで,式(39)に注目してみましょう。この式は,下界を表しています。つまり,私たちが目指すのは,式(39)の最大化です。
第1項目は,「$q$による対数尤度の期待値」を表しています。つまり,第1項目を最大化するアイディアは,対数尤度を最大化するアイディアと本質的には変わらないことがわかります。つまり,第1項目は最尤推定に相当するのです。
それでは,第1項目を最大化する$q$はどのような関数でしょうか。それは,対数尤度$\ln p(\boldsymbol{X}| \boldsymbol{Z})$が最大となる$\hat{\boldsymbol{Z}}$で値をもつクロネッカーのデルタ関数$\delta(\boldsymbol{Z} – \hat{\boldsymbol{Z}})$を考えればOKです。
同じように,第2項目に注目してみましょう。私たちは式(39)を最大化したいのですから,第2項目は最小化を考えなくてはなりません。第2項目は,シンプルにKLダイバージェンスを表しています。手法Aで見たように,KLダイバージェンスの最小化は最尤推定をMAP推定的に正則化のペナルティを与える役割を果たします。
つまり,第1項目は「最尤推定的発想」,第2項目は「MAP推定(正則化)的発想」を表現していることが分かります。下界を最大化することは,第1項目を大きくする(最尤推定の効果を大きくする)か,第2項目を小さくする(正則化の効果を大きくする)かのバランスを取っていることが分かるのです。以上をまとめます。
GMM(混合ガウス分布)への適用
それでは,ここからは変分ベイズを実際にGMMのパラメータ推論に適用していこうと思います。まずは,流れを確認したいと思います。
【GMMへの適用の流れ】
1.同時分布のグラフィカルモデル(依存関係)を確認
2.平均場近似のグループ分けを仮定
3.式(18)を利用して更新式を導出
4.更新式を繰り返し用いることで下界を最大化する
グラフィカルモデル
さて,早速GMMのグラフィカルモデルを確認しましょう。GMMのパラメータは,潜在変数も含めると,$\boldsymbol{Z}, \boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda}$です。今回仮定する依存関係は,一般的によく利用されるものです。以下にグラフィカルモデルを示します。
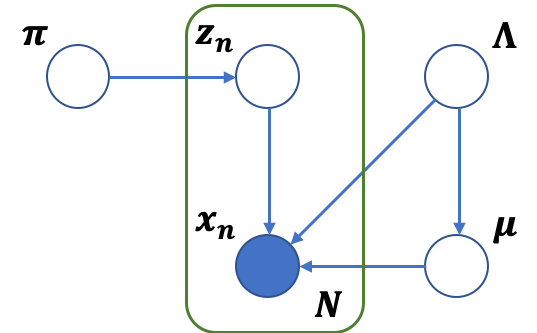 GMMのグラフィカルモデル
GMMのグラフィカルモデルこれを数式を用いて表すと,以下のようになります。
p(\boldsymbol{X}, \boldsymbol{Z}, \boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda}) &=& p(\boldsymbol{X} | \boldsymbol{Z}, \boldsymbol{\mu}, \boldsymbol{\Lambda}) p(\boldsymbol{Z} | \boldsymbol{\pi}) p(\boldsymbol{\pi}) p(\boldsymbol{\mu} | \boldsymbol{\Lambda}) p(\boldsymbol{\Lambda})
\end{eqnarray}
ここで,各分布は以下のように定めると仮定します。
p(\boldsymbol{X} | \boldsymbol{Z}, \boldsymbol{\mu}, \boldsymbol{\Lambda})
&=& \prod_{n=1}^{N} \prod_{k=1}^{K} \mathcal{N} (\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k^{-1}) \\
p(\boldsymbol{Z} | \boldsymbol{\pi})
&=& \prod_{n=1}^{N} \prod_{k=1}^{K} \pi_k^{z_{nk}} \\
p(\boldsymbol{\pi})
&=& \rm{Dir}(\boldsymbol{\pi} | \boldsymbol{\alpha_0}) \\
p(\boldsymbol{\mu} | \boldsymbol{\Lambda})
&=& \prod_{k=1}^K \mathcal{N}(\boldsymbol{\mu}_k | \boldsymbol{m}_0, (\beta_0 \boldsymbol{\Lambda}_k)^{-1}) \\
p(\boldsymbol{\Lambda})
&=& \prod_{k=1}^{K} \mathcal{W}(\boldsymbol{\Lambda}_k | \boldsymbol{W}_0, \nu_0)
\end{eqnarray}
簡単に,なぜこのような仮定を置くのかの根拠を説明しておきます。$\boldsymbol{Z}$の条件付き分布は,$z$と$\pi$の性質から自然に導かれる関係です。つまり,$\boldsymbol{z}$はone-hot-vector(ある要素だけ1で他は0)ですので,$\boldsymbol{z}$の生成確率を$\pi$を利用して表現すれば,上のように累乗と総乗で表すことができるのです。
データの条件付き確率も同様に,$\boldsymbol{z}$がone-hot-vectorであることを利用して表現できます。$\boldsymbol{\pi}$の事前分布がディリクレ分布であるのは,$p(\boldsymbol{Z} | \boldsymbol{\pi})$が多項分布の形(n=1のカテゴリカル分布)をしており,その共役事前分布として定めているからです。同様に,多変量正規分布$p(\boldsymbol{X} | \boldsymbol{Z}, \boldsymbol{\mu}, \boldsymbol{\Lambda})$の共役事前分布として$p(\boldsymbol{\mu} | \boldsymbol{\Lambda})p(\boldsymbol{\Lambda})$には,ガウスウィシャート分布を仮定しています。
以下では,ここで定義した分布を使って計算していくため,定義を確認しておきましょう。具体的には,ディリクレ分布,多変量ガウス分布,ウィシャート分布の定義を知っておく必要があります。また,のちに期待値と対数幾何平均($E[\ln x]$)を利用することになるため,ここで一緒に確認しておきましょう。
【ディリクレ分布】
\rm{Dir}(\boldsymbol{\pi} | \boldsymbol{\alpha_0})
&=& C(\boldsymbol{\alpha}_0) \prod_{k=1}^{K} \pi_k ^{\alpha_0 – 1} \\
E[\pi_k] &=& \frac{\alpha_k}{\hat{\alpha}}\\
E[\ln \pi_k] &=& \psi(\alpha_k) – \psi(\hat{\alpha})
\end{eqnarray}
ただし,$\hat{\alpha}, C(\cdot), \psi(\cdot)$は以下のように定義されます。
\begin{eqnarray}
\hat{\alpha} &=& \sum_{k=1}^{K} \alpha_k \\
C(\boldsymbol{\alpha}) &=& \frac{\Gamma(\hat{\alpha})}{\prod_{k=1}^{K} \Gamma(\alpha_k)} \\
\psi(a) &=& \frac{\rm{d}}{\rm{d}a} \ln \Gamma(a)
\end{eqnarray}
ちなみに,ガンマ関数($\Gamma(a)$)の定義は以下の通りで,階乗の一般化として捉えられます。
\begin{eqnarray}
\Gamma(a) &=& \int_0^{\infty} t^{a-1} e^{-t} \rm{d}t
\end{eqnarray}
続いて,多変量ガウス分布です。こちらは大丈夫だと思います。
【多変量ガウス分布】
\mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}, \boldsymbol{\Sigma})
&=& \frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{|\boldsymbol{\Sigma}|^{\frac{1}{2}}} \exp\{ -\frac{1}{2} (\boldsymbol{x} – \boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x} – \boldsymbol{\mu}) \} \\
E[\boldsymbol{x}] &=& \boldsymbol{\mu}
\end{eqnarray}
最後に,ウィシャート分布です。
【ウィシャート分布】
\mathcal{W}(\boldsymbol{\Lambda} | \boldsymbol{W}, \nu)
&=& B(\boldsymbol{W}, \nu)|\Lambda|^{\frac{\nu – D – 1}{2}} \exp(-\frac{1}{2} Tr[\boldsymbol{W}^{-1}\boldsymbol{\Lambda}])\\
E[\boldsymbol{\Lambda}] &=& \nu \boldsymbol{W} \\
E[\ln |\boldsymbol{\Lambda}|] &=& \sum_{i=1}^{D} \psi(\frac{\nu + 1 – i}{2}) + D \ln 2 + \ln |\boldsymbol{W}|
\end{eqnarray}
$\psi(\cdot)$は上で定義した通りです。また,$B(\cdot)$は,以下のように定義されます。
B(\boldsymbol{W}, \nu) &=& |\boldsymbol{W}|^{-\frac{\nu}{2}}\{ 2^{\frac{\nu D}{2}} \pi^{\frac{D(D-1)}{4}} \prod_{i=1}^{D}\Gamma(\frac{\nu + 1 – i}{2}) \}^{-1}
\end{eqnarray}
平均近似場のグループ分け
さて,ここまでで「ステップ1」が終了です。続いて,平均近似場のグループ分け(ステップ2)を考えていきましょう。ここでは,潜在変数と他のパラメータは別々のグループに排反に分かれることを仮定しましょう。
\begin{eqnarray}
q(\boldsymbol{Z}, \boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda}) &=& q(\boldsymbol{Z}) q(\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda})
\end{eqnarray}
さて,「ステップ2」まで終了しました。続いて,変分ベイズ法の一般的な結果である式(18)を利用して,具体的な更新式を導きたいと思います。なかなか大変な計算が続きますが,丁寧に行間を詰めていこうと思いますので,頑張って計算していきましょう。
潜在変数に関する最適化
まずは,最適な$q$である$q^{\ast} (\boldsymbol{Z})$から導出を始めます。式(18)を利用すれば,以下のように式を展開できます。
\ln q^{\ast} (\boldsymbol{Z}) &=& E_{\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda}} [\ln p(\boldsymbol{X}, \boldsymbol{Z}, \boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda})] + \rm{const} \\
&\overset{\boldsymbol{Z}}{=}& E_{\boldsymbol{\pi}} [\ln p(\boldsymbol{Z} | \boldsymbol{\pi} )] + E_{\boldsymbol{\mu}, \boldsymbol{\Lambda}}[p(\boldsymbol{X} | \boldsymbol{Z}, \boldsymbol{\mu}, \boldsymbol{\Lambda})] + \rm{const} \\
&=& \sum_{n=1}^{N} \sum_{k=1}^{K} z_{nk} \{ E[\ln \pi_k] + \frac{1}{2} E[\ln |\boldsymbol{\Lambda}_k|] – \frac{D}{2} \ln (2\pi) \notag \\
&&- E_{\boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k} [(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \boldsymbol{\Lambda}_k (\boldsymbol{x}_n – \boldsymbol{\mu}_k)] \} + \rm{const} \\
&=& \sum_{n=1}^{N} \sum_{k=1}^{K} z_{nk} \ln \rho_{nk} + \rm{const}
\end{eqnarray}
ただし,ごちゃごちゃしている$\rho_{nk}$は以下のように置きました。
\ln \rho_{nk} &=& E[\ln \pi_k] + \frac{1}{2} E[\ln |\boldsymbol{\Lambda}_k|] – \frac{D}{2} \ln (2\pi) \notag \\
&& – E_{\boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k} [(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \boldsymbol{\Lambda}_k (\boldsymbol{x}_n – \boldsymbol{\mu}_k)]
\end{eqnarray}
一旦,定数項constを無視すると,以下のように変形できます。
\begin{eqnarray}
q^{\ast}(\boldsymbol{Z}) &\propto& \prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}}
\end{eqnarray}
以下では,厳密に$q^{\ast}(\boldsymbol{Z})$を定めるために,正規化定数$A$を求めていきたいと思います。
\begin{eqnarray}
A &=& \sum_{\boldsymbol{Z}} \prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}} \\
&=& \sum_{\boldsymbol{z}_1} \prod_{k=1}^{K} \rho_{1k}^{z_{1k}} \cdot\sum_{\boldsymbol{z}_2} \prod_{k=1}^{K} \rho_{2k}^{z_{2k}} \cdots \\
&=& \sum_{k} \rho_{1k} \cdot \sum_{k} \rho_{2k} \cdots \\
&=& \prod_{n=1}^{N} \sum_{k=1}^{K}\rho_{nk}
\end{eqnarray}
このように,正規化定数が求まりました。したがって,$q^{\ast}(\boldsymbol{Z})$は正確に以下のように表されます。
q^{\ast}(\boldsymbol{Z}) &=& \frac{\prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}}}{A}\\
&=& \frac{\prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}}}{\prod_{n=1}^{N} \sum_{k=1}^{K}\rho_{nk}}\\
&=& \prod_{n=1}^{N} \frac{\prod_{k=1}^{K} \rho_{nk}^{z_{nk}}}{\sum_{k=1}^{K}\rho_{nk}} \\
&=& \prod_{k=1}^{N} \frac{\prod_{k=1}^{K} \rho_{nk}^{z_{nk}}}{\prod_{k=1}^{K}\{ \sum_{k=1}^{K}\rho_{nk} \}^{z_{nk}} }\\
&=& \prod_{n=1}^{N} \prod_{k=1}^{K}\{ \frac{\rho_{nk}}{\sum_{k=1}^{K} \rho_{nk}} \}^{z_{nk}} \\
&=& \prod_{n=1}^{N} \prod_{k=1}^{K} r_{nk}^{z_{nk}}
\end{eqnarray}
ただし,$r_{nk}$は以下のように置きました。
\begin{eqnarray}
r_{nk} = \frac{\rho_{nk}}{\sum_{j=1}^K \rho_{nj}}
\end{eqnarray}
実は,この$r_{nk}$がEMアルゴリズムにおける負担率となります。その証明としては,式(75)の期待値が$r_{nk}$となることから確認できます。
つまり,以下のような関係性が成り立ちます。この式は,EMアルゴリズムで定義した負担率と全く同じです。
\begin{eqnarray}
E[z_{nk}] &=& r_{nk}
\end{eqnarray}
さて,具体的に$r_{nk}$を計算するために,$\rho_{nk}$を求めてしまいましょう。式(64)の$\rho$の定義と事前分布の仮定から,変形をすることができます。
\ln \rho_{nk} &=& E[\ln \pi_k] + \frac{1}{2} E[\ln |\boldsymbol{\Lambda}_k|] – \frac{D}{2} \ln (2\pi) \notag \\
&& – \frac{1}{2} E_{\boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k} [(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \boldsymbol{\Lambda}_k (\boldsymbol{x}_n – \boldsymbol{\mu}_k)] \\
&=& \{ \psi (\alpha_k) – \psi (\hat{\alpha}) \} \notag \\
&& + \frac{1}{2} \{ \sum_{i=1}^{D} \psi(\frac{\nu_k + 1 – i}{2}) + D \ln (2) + \ln |\boldsymbol{W}_k| \} \notag \\
&& – \frac{1}{2} \{ D \beta_k^{-1} + \nu_k(\boldsymbol{x}_n – \boldsymbol{m}_k)^T \boldsymbol{W}_k(\boldsymbol{x}_n – \boldsymbol{m}_k) \} \\
&=& \ln \tilde{\pi}_k + \ln \tilde{\Lambda}_k – \frac{1}{2}\{ D \beta_k^{-1} + \nu_k(\boldsymbol{x}_n – \boldsymbol{m}_k)^T \boldsymbol{W}_k(\boldsymbol{x}_n – \boldsymbol{m}_k) \}
\end{eqnarray}
ただし,恒例ですが,ごちゃごちゃした項は以下のように置き換えました。
\ln \tilde{\pi}_k &=& E[\ln \pi_k] \\
&=& \psi (\alpha_k) – \psi (\hat{\alpha}) \\
\ln \tilde{\Lambda}_k &=& \frac{1}{2}E[\ln |\boldsymbol{\Lambda}_k|] \\
&=& \sum_{i=1}^{D} \psi(\frac{\nu_k + 1 – i}{2}) + D \ln (2) + \ln |\boldsymbol{W}_k|
\end{eqnarray}
この$\rho_{nk}$を計算して$r_{nk}$を求めておくことが,変分ベイズにおけるEステップになります。最後に,ダイレクトに$r_{nk}$を更新できるような式を求めておきましょう。式(80)の定義から$\rho$を求めます。$\rho$さえ求まれば,あとは正規化するだけで負担率$r_{nk}$が計算できます。
\rho_{nk} &=& \exp \{ \ln \tilde{\pi}_k + \frac{1}{2}\ln \tilde{\boldsymbol{\Lambda}}_k – \frac{1}{2}\{ D \beta_k^{-1} + \nu_k(\boldsymbol{x}_n – \boldsymbol{m}_k)^T \boldsymbol{W}_k(\boldsymbol{x}_n – \boldsymbol{m}_k) \} \} \\
&=& \tilde{\pi}_k \tilde{\boldsymbol{\Lambda}}_k ^{\frac{1}{2}} \exp \{- \frac{D}{2 \beta_k} – \frac{\nu_k}{2}(\boldsymbol{x}_n – \boldsymbol{m}_k)^T \boldsymbol{W}_k(\boldsymbol{x}_n – \boldsymbol{m}_k) \}
\end{eqnarray}
さて,変分ベイズのEステップをまとめておきましょう。
以下の2つの式を利用して負担率$r_{nk}$を計算する。
r_{nk} &=& \frac{\rho_{nk}}{\sum_{j=1}^K \rho_{nj}}\\
\rho_{nk}
&=& \tilde{\pi}_k \tilde{\boldsymbol{\Lambda}}_k ^{\frac{1}{2}} \exp \{- \frac{D}{2 \beta_k} – \frac{\nu_k}{2}(\boldsymbol{x}_n – \boldsymbol{m}_k)^T \boldsymbol{W}_k(\boldsymbol{x}_n – \boldsymbol{m}_k) \}
\end{eqnarray}
パラメータの最適化
続いて,変部ベイズのMステップです。Mステップでは,潜在変数以外のパラメータ(の分布)に関して最適化を施していきます。もちろん,また式(18)を利用していきます。
と,その前に。やや天下り的ですが,Eステップで計算した負担率($r_{nk}$)を用いて表すことができる統計量を定義しておきましょう。これらを先に定めておくことで,煩雑な式をシンプルに書き表すことができます。
N_k &=& \sum_{n=1}^{N} r_{nk} \\
\overline{x}_k &=& \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} \boldsymbol{x}_n \\
\boldsymbol{S}_k &=& \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} (\boldsymbol{x}_n – \overline{\boldsymbol{x}}_k) (\boldsymbol{x}_n – \overline{\boldsymbol{x}}_k)^T
\end{eqnarray}
さて,式(18)を利用するためには,$\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda}$の対数同時分布を知る必要があります。それは,式(40)の仮定と式(43)から(45)の仮定を利用すれば分かります。残念ながら,$\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda}$は式(40)の右辺の全ての項に出現していますので,全ての項について考えなくてはいけません。
\ln p(\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda})
&=& \ln p(\boldsymbol{X} | \boldsymbol{Z}, \boldsymbol{\mu}, \boldsymbol{\Lambda}) + \ln p(\boldsymbol{Z} | \boldsymbol{\pi}) \notag \\
&& + \ln p(\boldsymbol{\pi}) + \ln p(\boldsymbol{\mu} | \boldsymbol{\Lambda}) + \ln p(\boldsymbol{\Lambda}) \\
\end{eqnarray}
こちらの式を利用すれば,式(18)の一般的な結果が利用できます。
\ln q^{\ast} (\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda})
&=& E_{\boldsymbol{Z}}[\ln p(\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Lambda})]\\
&=& \sum_{k=1}^{K} \sum_{n=1}^{N} E[z_{nk}] \ln \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Lambda}^{-1}) + E_{\boldsymbol{Z}}[\ln p(\boldsymbol{Z} | \boldsymbol{\pi})] \notag \\
&& + \ln p(\boldsymbol{\pi}) + \sum_{k=1}^{K} \ln p(\boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k) + \rm{const}
\end{eqnarray}
以下では,$\boldsymbol{\pi}$と$\boldsymbol{\mu}, \boldsymbol{\Lambda}$に分けてパラメータの更新式を導出したいと思います。方針としては,式(94)のうち,最初に$\boldsymbol{\pi}$に関わる部分を抽出します。その形が実は「ディリクレ分布の対数形」となっているため,係数比較からパラメータの更新式を求めることができます。
$\boldsymbol{\mu}, \boldsymbol{\Lambda}$も同様に導出します。しかし,こちらは$\boldsymbol{\pi}$のように一筋縄にはいきません。後ほど説明しますが,ベイズの定理を利用して地道に計算をしていかなくてはいけません。最終的に係数比較を利用する点は変わりません。
さて,早速$\boldsymbol{\pi}$から計算を始めましょう。式(94)に式(43)から(45)の仮定を代入して,$\boldsymbol{\pi}$に関係する項だけを取り出します。すると,それは$q^{\ast}(\boldsymbol{\pi})$を表していますよね。
\ln q^{\ast}(\boldsymbol{\pi}) &=& \ln C(\boldsymbol{\alpha}_0) \prod_{k=1}^{K} \pi_k ^{\alpha_0 – 1} + \sum_{k=1}^{K} \sum_{n=1}^{N} r_{nk} \ln \pi_k +\rm{const}\\
&=& (\alpha_0 – 1)\sum_{k=1}^{K} \ln \pi + \sum_{k=1}^{K} \sum_{n=1}^{N} r_{nk} \ln \pi_k +\rm{const}\\
&=& (\alpha_0 + N_k – 1)\sum_{k=1}^{K} \ln \pi_k + \rm{const}
\end{eqnarray}
ちなみに,以下の定義を利用しました。
\begin{eqnarray}
N_k &=& \sum_{n=1}^{N} r_{nk} \\
&=& \sum_{n=1}^{N} E[z_{nk}]
\end{eqnarray}
先ほどもお伝えした通り,この形はディリクレ分布の対数をとったものになっています。
\ln \rm{Dir}(\boldsymbol{\pi} | \boldsymbol{\alpha}) = (\alpha_k – 1) \sum_{k=1}^{K} \ln \pi_k + const
\end{eqnarray}
これらの係数を比較することにより,以下のような更新式を得ることができます。
\begin{eqnarray}
q^{\ast}(\boldsymbol{\pi}) &=& \rm{Dir}(\boldsymbol{\pi} | \boldsymbol{\alpha}) \\
\boldsymbol{\alpha} &=& \{ \alpha_0, \cdots, \alpha_K \} \\
\alpha_k &=& \alpha_0 + N_k
\end{eqnarray}
これにて,とりあえず$\boldsymbol{z}$に関する更新は終了です。
さて,いよいよ変分ベイズのGMMへの適用もクライマックスです。これからの計算が一番煩雑なので,少し覚悟してください。流れは,先ほどもお伝えした通り,式(94)に式(43)から(45)の仮定を代入して,$\boldsymbol{\mu},\boldsymbol{\Lambda} $に関係する項だけを取り出します。
\ln q^{\ast}(\boldsymbol{\mu}, \boldsymbol{\Lambda})
&=& \sum_{k=1}^{K} \ln \mathcal{N}(\boldsymbol{\mu} | \boldsymbol{m}_0, (\beta_0 \boldsymbol{\Lambda}_k)^{-1}) + \sum_{k=1}^{K} \ln \mathcal{W}(\boldsymbol{\Lambda}_k | \boldsymbol{W}_0, \boldsymbol{\nu}_0) \notag \\
&+& \sum_{n=1}^{N} \sum_{k=1}^{K} E[z_{nk}] \ln \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k^{-1}) + \rm{const} \\
&\propto& \sum_{k=1}^{K} \{ \frac{1}{2} \ln |\beta_0 \boldsymbol{\Lambda}_k| – \frac{1}{2} (\boldsymbol{\mu}_k – \boldsymbol{m}_0)^T \beta_0 \boldsymbol{\Lambda}_k (\boldsymbol{\mu}_k – \boldsymbol{m}_0) \notag \\
&+& \frac{\boldsymbol{\nu}_0 – D – 1}{2} \ln |\boldsymbol{\Lambda}_k| – \frac{1}{2} Tr(\boldsymbol{W}_0 \boldsymbol{\Lambda}_k) \notag \\
&+& \frac{1}{2} N_k \ln |\boldsymbol{\Lambda}_k| – \frac{1}{2} \sum_{n=1}^{N} r_{nk} (\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \boldsymbol{\Lambda}_k (\boldsymbol{x}_n – \boldsymbol{\mu}_k) \}
\end{eqnarray}
ここで注意するべきなのは,最後の項で早とちりして$\sum_{n=1}^{N}r_{nk}=N_k$と変形してしまわないことです。なぜなら,$\sum_n$の中身に$\boldsymbol{x}_n$が含まれているため,$N_k$の定義とは一致しないからです。ここは,引っかかりポイントだと思います。
先に,$\boldsymbol{\mu}$に関する項を取り出します。ベイズの定理より,
\ln q^{\ast}(\boldsymbol{\mu},\boldsymbol{\Lambda})
&=& \ln q^{\ast}(\boldsymbol{\mu}|\boldsymbol{\Lambda}) + \ln q^{\ast}(\boldsymbol{\Lambda})
\end{eqnarray}
となりますので,$\boldsymbol{\mu}$に関係する項だけを取り出した結果は$\ln q^{\ast}(\boldsymbol{\mu}|\boldsymbol{\Lambda})$となることが分かります。先ほどの結果を流用します。
\ln q^{\ast}(\boldsymbol{\mu}|\boldsymbol{\Lambda}) &=&
\sum_{k=1}^{K} \{ – \frac{1}{2} (\boldsymbol{\mu}_k – \boldsymbol{m}_0)^T \beta_0 \boldsymbol{\Lambda}_k (\boldsymbol{\mu}_k – \boldsymbol{m}_0) \notag \\
&& – \frac{1}{2} N_k (\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \boldsymbol{\Lambda}_k (\boldsymbol{x}_n – \boldsymbol{\mu}_k) \}
\end{eqnarray}
この中で,$\boldsymbol{\mu}_k$の二次の項である$\boldsymbol{\mu}_k^T \boldsymbol{\mu}_k$の係数を取り出してみます。
– \frac{1}{2}\boldsymbol{\mu}_k^T \beta_0 \boldsymbol{\Lambda}_k \boldsymbol{\mu}_k – \frac{1}{2} N_{k} \boldsymbol{\mu}_k^T \boldsymbol{\Lambda}_k \boldsymbol{\mu}_k = – \frac{1}{2} \boldsymbol{\mu}_k^T (\beta_o \boldsymbol{\Lambda}_k + N_k\boldsymbol{\Lambda}_k)\boldsymbol{\mu}_k
\end{eqnarray}
この形,多変量ガウス分布における$\boldsymbol{\mu}_k^T \boldsymbol{\mu}_k$の対数形の係数と一致していますよね。つまり,以下のような関係が成り立っています。
\ln q^{\ast}(\boldsymbol{\mu}|\boldsymbol{\Lambda})
&=& \ln \mathcal{N}(\boldsymbol{\mu}_k | \boldsymbol{m}_k, \beta_k \boldsymbol{\Lambda}_k)
\end{eqnarray}
先ほどと同じように係数を比較すれば,以下のような更新式を得られます。
\begin{eqnarray}
\beta_k = \beta_0 + N_k
\end{eqnarray}
$\boldsymbol{\mu}_k$の一次の項である$\boldsymbol{\mu}_k^T$についても,同様に係数を取り出してみます。
\boldsymbol{\mu}_k^T \beta_0 \boldsymbol{\Lambda}_k \boldsymbol{m}_0 + \sum_{n=1}^{N} r_{nk} \boldsymbol{\mu}_k^T \boldsymbol{\Lambda}_k \boldsymbol{x}_n
&=& \boldsymbol{\mu}_k^T \boldsymbol{\Lambda}_k \{ \beta_0 m_0 + N_k \overline{\boldsymbol{x}}_k \}
\end{eqnarray}
例のごとく,しっかりと多変量ガウス分布の対数形と一致しています。係数を比較することで,更新式を手に入れましょう。
\begin{eqnarray}
\boldsymbol{m}_k = \frac{1}{\beta_k} (\beta_0 \boldsymbol{m}_0 + N_k \overline{\boldsymbol{x}}_n)
\end{eqnarray}
最後は,$\boldsymbol{\Lambda}$に関して係数を比較していきたいと思います。先ほどのベイズの定理による展開を利用すれば,$\ln q^{\ast}(\boldsymbol{\Lambda})$は以下のように表すことができます。
\ln q^{\ast}(\boldsymbol{\Lambda})
&=& \ln q^{\ast}(\boldsymbol{\mu},\boldsymbol{\Lambda}) – \ln q^{\ast}(\boldsymbol{\mu}|\boldsymbol{\Lambda})
\end{eqnarray}
式(105)から式(109)を引きます。$\frac{1}{2} \ln |\boldsymbol{\Lambda}_k|$だけ打ち消しあってくれます。また,ここがキモになるのですが,のちにウィシャート分布の形を出現させたいため,$\ln |\boldsymbol{\Lambda}_k|$以外の項は全てトレースに突っ込んでしまいます。利用するトレースの公式は以下の通りです。
\begin{eqnarray}
\boldsymbol{x}^T \boldsymbol{A} \boldsymbol{x}
&=& Tr[\boldsymbol{A} \boldsymbol{x} \boldsymbol{x}^T]
\end{eqnarray}
さて,計算していきましょう。
\ln q^{\ast}(\boldsymbol{\Lambda})
&=& \sum_{k=1}^{K} \{ \frac{1}{2} \ln |\beta_0 \boldsymbol{\Lambda}_k| – \frac{1}{2} (\boldsymbol{\mu}_k – \boldsymbol{m}_0)^T \beta_0 \boldsymbol{\Lambda}_k (\boldsymbol{\mu}_k – \boldsymbol{m}_0) \notag \\
&& + \frac{\boldsymbol{\nu}_0 – D – 1}{2} \ln |\boldsymbol{\Lambda}_k| – \frac{1}{2} Tr(\boldsymbol{W}_0 \boldsymbol{\Lambda}_k) \notag \\
&& + \frac{1}{2} N_k \ln |\boldsymbol{\Lambda}_k| – \frac{1}{2} \sum_{n=1}^{N} r_{nk} (\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \boldsymbol{\Lambda}_k (\boldsymbol{x}_n – \boldsymbol{\mu}_k) \notag \\
&& – \frac{1}{2}|\boldsymbol{\Lambda}_k| +\frac{\beta_k}{2} (\boldsymbol{\mu}_k – \boldsymbol{m}_k)^T \boldsymbol{\Lambda}_k (\boldsymbol{\mu}_k – \boldsymbol{m}_k)\} \\
&=& \frac{\nu_k – D – 1}{2} \ln |\boldsymbol{\Lambda}_k| – \frac{1}{2}Tr[\boldsymbol{\Lambda}\boldsymbol{W}_k^{-1}]
\end{eqnarray}
ここで,$\nu_k$と$\boldsymbol{W}_k^{-1}$はごちゃごちゃした項をひとつにまとめた項です。なぜ$\nu_k$と$\boldsymbol{W}_k^{-1}$のように「更新式の対象」として置けるのかというと,式(116)がウィシャート分布の対数をとった形になっているからです。
ですから,式(115)から式(116)の置き換えを求めることで,$\nu_k$と$\boldsymbol{W}_k^{-1}$に関する更新式を手に入れることができます。さて,最初に簡単な$\nu_k$の方からみていきましょう。$\ln |\boldsymbol{\Lambda}_k|$の係数に注目すれば,以下のような関係式が導かれます。
\begin{eqnarray}
\nu_k = \nu_0 + N_k
\end{eqnarray}
さて,次は$\boldsymbol{W}_k^{-1}$に関してです。ここでは,先ほどのトレースの公式を利用します。
\boldsymbol{W}^{-1} &=& \beta_0 (\boldsymbol{\mu}_k – \boldsymbol{m}_0)(\boldsymbol{\mu}_k – \boldsymbol{m}_0)^T + \boldsymbol{W}_0^{-1} \notag \\
&& + \sum_{n=1}^{N} r_{nk }(\boldsymbol{x}_n – \boldsymbol{\mu}_k)(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T – \beta_k (\boldsymbol{\mu}_k – \boldsymbol{m}_k)(\boldsymbol{\mu}_k – \boldsymbol{m}_k)^T
\end{eqnarray}
この式を,式(89)から式(91)を使って綺麗にしていきます。その際,ポイントとなるのは,$\boldsymbol{\mu}_k$の項は打ち消されるという点です。実際に,$\beta_k = \beta_0 + N_k$ を利用すれば計算しても示すことができますが,今回は$\ln q^{\ast}(\boldsymbol{\Lambda})$を考えていますので,$\boldsymbol{\mu}_k$は「消えるはず」なんです。
そこで,以下では$\boldsymbol{\mu}_k$の項を無視して考えていきます。以下の関係式を利用します。
\sum_{n=1}^{N} r_{nk}\boldsymbol{x}_n \boldsymbol{x}_n^T
&=& \sum_{n=1}^{N} r_{nk}(\boldsymbol{x}_n – \overline{\boldsymbol{x}}_k)(\boldsymbol{x}_n – \overline{\boldsymbol{x}}_k)^T \notag \\
&& + 2 \sum_{n=1}^{N} r_{nk} \boldsymbol{x}_n \overline{\boldsymbol{x}}_k – \sum_{n=1}^{N} r_{nk} \overline{\boldsymbol{x}}_k \overline{\boldsymbol{x}}_k^T\\
&=& \sum_{n=1}^{N} r_{nk}(\boldsymbol{x}_n – \overline{\boldsymbol{x}_k})(\boldsymbol{x}_n – \overline{\boldsymbol{x}_k})^T + 2 N_k \overline{\boldsymbol{x}}_k \overline{\boldsymbol{x}}_k^T – \overline{\boldsymbol{x}}_k \overline{\boldsymbol{x}}_k^T\\
&=& \sum_{n=1}^{N} r_{nk}(\boldsymbol{x}_n – \overline{\boldsymbol{x}}_k)(\boldsymbol{x}_n – \overline{\boldsymbol{x}}_k)^T + N_k \overline{\boldsymbol{x}}_k \overline{\boldsymbol{x}}_k^T \\
&=& N_k \boldsymbol{S}_k + N_k \overline{\boldsymbol{x}}_k \overline{\boldsymbol{x}}_k^T
\end{eqnarray}
また,式(110)と式(112)の$\beta_k$と$\boldsymbol{m}_k$の更新式も利用します。それでは,式(117)を変形していきましょう。先ほどもお伝えしましたが,$\boldsymbol{\mu}_k$を含む項を無視するのがポイントです。
\boldsymbol{W}_k^{-1}
&=& \boldsymbol{W}_0^{-1} + \beta_0 \boldsymbol{m}_0 \boldsymbol{m}_0^T + \sum_{n=1}^N \boldsymbol{x}_n \boldsymbol{x}_n^T – \beta_k \boldsymbol{m}_k \boldsymbol{m}_k^T \\
&=& \boldsymbol{W}_0^{-1} + \beta_0 \boldsymbol{m}_0 \boldsymbol{m}_0^T \notag \\
&& + (N_k \boldsymbol{S}_k + N_k \overline{\boldsymbol{x}}_k \overline{\boldsymbol{x}}_k^T) – \beta_k \boldsymbol{m}_k \boldsymbol{m}_k^T \\
&=& \boldsymbol{W}_0^{-1} + N_k \boldsymbol{S}_k \notag \\
&& +\beta_0 \boldsymbol{m}_0 \boldsymbol{m}_0^T + N_k \overline{\boldsymbol{x}}_k \overline{\boldsymbol{x}}_k^T \notag \\
&& – (\beta_0 + N_k) \cdot \frac{1}{(\beta_0 + N_k)^2}(\beta_0 \boldsymbol{m}_0 + N_k \overline{\boldsymbol{x}}_k) (\beta_0 \boldsymbol{m}_0^T + N_k \overline{\boldsymbol{x}}_k^T) \\
&=& \boldsymbol{W}_0^{-1} + N_k \boldsymbol{S}_k \notag \\
&& + \frac{1}{\beta_0 + N_k} \{ (\beta_0 + N_k)(\beta_0 \boldsymbol{m}_0 \boldsymbol{m}_0^T + N_k \overline{\boldsymbol{x}}_k \overline{\boldsymbol{x}}_k^T) – (\beta_0 \boldsymbol{m}_0 + N_k \overline{\boldsymbol{x}}_k)(\beta_0 \boldsymbol{m}_0^T + N_k \overline{\boldsymbol{x}}_k^T) \} \\
&=& \boldsymbol{W}_0^{-1} + N_k \boldsymbol{S}_k \notag \\
&& + \frac{\beta_0 N_k}{\beta_0 + N_k} (\overline{\boldsymbol{x}}_k – \boldsymbol{m}_0)(\overline{\boldsymbol{x}}_k – \boldsymbol{m}_0)^T
\end{eqnarray}
以上より,$\boldsymbol{W}_k^{-1}$の更新式は以下のように表されます。
\boldsymbol{W}_k^{-1}
&=& \boldsymbol{W}_0^{-1} + N_k \boldsymbol{S}_k + \frac{\beta_0 N_k}{\beta_0 + N_k} (\overline{\boldsymbol{x}}_k – \boldsymbol{m}_0)(\overline{\boldsymbol{x}}_k – \boldsymbol{m}_0)^T
\end{eqnarray}
本当にお疲れ様でした!!以上で,全てのパラメータの更新式が手に入りました。一旦,Mステップについてまとめた後に,全体の流れをまとめていきます。
Eステップで計算した負担率$r_{nk}$を利用して,各パラメータの更新式を計算する。
N_k &=& \sum_{n=1}^{N} r_{nk} \\
\overline{x}_k &=& \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} \boldsymbol{x}_n \\
\boldsymbol{S}_k &=& \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} (\boldsymbol{x}_n – \overline{\boldsymbol{x}}_k) (\boldsymbol{x}_n – \overline{\boldsymbol{x}}_k)^T \\
\alpha_k &=& \alpha_0 + N_k \\
\beta_k &=& \beta_0 + N_k \\
\boldsymbol{m}_k &=& \frac{1}{\beta_k} (\beta_0 \boldsymbol{m}_0 + N_k \overline{\boldsymbol{x}}_n) \\
\nu_k &=& \nu_0 + N_k \\
\boldsymbol{W}_k^{-1}
&=& \boldsymbol{W}_0^{-1} + N_k \boldsymbol{S}_k + \frac{\beta_0 N_k}{\beta_0 + N_k} (\overline{\boldsymbol{x}}_k – \boldsymbol{m}_0)(\overline{\boldsymbol{x}}_k – \boldsymbol{m}_0)^T
\end{eqnarray}
まとめ
最後に,変分ベイズのまとめです。
1.初期値設定
2.(Eステップ)負担率$r_{nk}$の計算
3.(Mステップ)各パラメータの更新
4.収束判定
実装
以下では,10000個の3次元データをGMMーVB(変分ベイズによる混合ガウス分布の推論)を利用してクラスタリングする実装例をお伝えしていこうと思います。EMアルゴリズムの実装例では,クラスを定義せずにひたすら関数を定義していきましたが,今回はしっかりと「変分ベイズクラス」を定義して,オブジェクト指向の考え方に則ってコーディングしていこうと思います。
必要なモジュール等のインポート
import csv
import numpy as np
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
from numpy import linalg as la
from scipy.special import digamma, gamma, logsumexp
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys特に珍しいものはインポートしていません。VBの計算にはディガンマ関数やガンマ関数,logsumexpが必要なので,scipyの力を借りたいと思います。
データのリスト化
txt_dir = "data.csv"
with open(txt_dir) as f:
reader = csv.reader(f)
l = [row for row in reader]
for i in range(len(l)):
for j in range(len(l[i])):
l[i][j] = float(l[i][j])
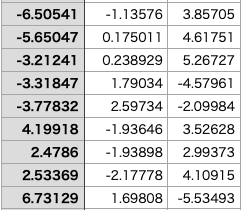
l = np.array(l)データを読み込みます。以下ではNumpyを活用するので,Numpy.ndarrayに変換しておきます。ちなみに,data.csvは以下のような3次元座標のデータの集まりになっています。
クラスの定義
class VBGMM():
def __init__(self, K=6, alpha0=0.1):
self.K = K
self.alpha0 = alpha0
以下では,VBGMMクラスのメソッドを定義していきます。最初に,コンストラクタとして,クラスタの個数$K$とディリクレ分布のハイパーパラメータ$\alpha_0$を定義します。
パラメータの初期化
def init_params(self, X):
self.N, self.D = X.shape
self.m0 = np.random.randn(self.D)
self.beta0 = np.array([1.0])
self.W0 = np.eye(self.D)
self.nu0 = np.array([self.D])
self.N_k = (self.N / self.K) + np.zeros(self.K)
self.alpha = np.ones(self.K) * self.alpha0
self.beta = np.ones(self.K) * self.beta0
self.m = np.random.randn(self.K, self.D)
self.W = np.tile(self.W0, (self.K, 1, 1))
self.nu = np.ones(self.K)*self.D
self.Mu = self.m
self.Sigma = np.zeros((self.K, self.D, self.D))
for k in range(self.K):
self.Sigma[k] = la.inv(self.nu[k] * self.W[k])
以下では,VBGMMクラス内のインデントが必要なことに注意してください。最初に定義するメソッドは,パラメータの初期化です。Nはサンプル数,Dは各データの次元です。今回は,N=10000, D=3のデータを用意しました。続いて,mは多変量ガウス分布(ガウスウィシャートの片っ方)の期待値です。標準正規分布からランダムに初期値を生成しています。
betaは多変量ガウス分布の制度行列の係数です。初期値は$1$で設定します。Wとnuはどちらもウィシャート分布のパラメータです。Wは単位行列,nuは次元の数として初期値を設定します。N_kは各クラスタに属する実質的なデータ数なので,初期値は全データ数をクラスタ数で当分したものを利用します。
その下には,実際にEステップで利用する最初のパラメータを更新してしまっています。こうすることで,Eステップを実行する際に,「self.hoge」を呼び出すだけでパラメータの更新ができます。
また,MuとSigmaですが,これは混合ガウス分布の期待値と共分散行列です。どこで定義しても良いですが,初期化の時点で一旦定めてしまおうと思います。
Eステップ
def e_step(self, X):
pi = digamma(self.alpha) - digamma(self.alpha.sum())
Lambda_tilde = np.zeros((self.K))
for k in range(self.K):
digamma_sum = np.array([])
for i in range(self.D):
digamma_sum = np.append(digamma_sum, digamma((self.nu[k] + 1 - i)/2))
A = np.sum(digamma_sum)
B = self.D * np.log(2)
C = np.log(la.det(self.W[k]))
Lambda_tilde[k] = A + B + C
rho = np.zeros((self.N, self.K))
for n in range(self.N):
for k in range(self.K):
gap = (X[n] - self.m[k])[:, None]
A = -(self.D/(2*self.beta[k]))
B = -(self.nu[k]/2)*(gap.T@self.W[k]@gap)
rho[n][k] = pi[k] + 0.5*Lambda_tilde[k] + A + B
r_log = rho - logsumexp(rho, axis=1)[:,None]
r = np.exp(r_log)
r[np.isnan(r)] = 1.0 / (self.K)
return r
上で導出したEステップを実装しています。ここでは,ポイントを絞って大事な点をお伝えしていこうと思います。私も引っかかったのですが,正規化は対数領域で行います。ここは非常に重要なポイントです。
指数領域のままで正規化を行うと,非常に小さい値で割り算を行うことになります。そうなると,オーバーフローをおこしてしまう危険性があります。実際に,私もオーバーフローを起こしてしまい,1日を費やしてしまいました。
一応,nanが出てきた際の例外処理も記述しておりますが,対数領域で正規化を行えば,基本的にnanが出てくることはありません。
Mステップ
def m_step(self, X, r):
self.N_k = np.sum(r, axis=0, keepdims=True).T
barx = (r.T @ X) / self.N_k
S_list = np.zeros((self.N, self.K, self.D, self.D))
for n in range(self.N):
for k in range(self.K):
gap = (X[n] - barx[k])[:, None]
S_list[n][k] = r[n][k] * gap @ gap.T
S = np.sum(S_list, axis=0) / self.N_k[:,None]
self.alpha = self.alpha0 + self.N_k
self.beta = self.beta0 + self.N_k
for k in range(self.K):
self.m[k] = (1/self.beta[k]) * (self.beta0 * self.m0 + self.N_k[k] * barx[k])
for k in range(self.K):
gap = (barx[k] - self.m0)[:, None]
A = la.inv(self.W0)
B = self.N_k[k] * S[k]
C = ((self.beta0*self.N_k[k]) / (self.beta0 + self.N_k[k])) * gap@gap.T
self.W[k] = la.inv(A + B + C)
self.nu[k] = self.nu0 + self.N_k[k]
pi = self.alpha / np.sum(self.alpha, keepdims=True)
return pi
Mステップを実装しています。ここでも,ポイントを絞って大切な点をお伝えしていきます。まず,引っかかりやすいのが次元の処理です。例えば,gapを定義する際に「[:, None]」を付けて次元を拡張しています。これは,後に行列計算を行うために,しっかりと行列の形にしておかなければならないためです。この処理を行わないと,うまく更新式が収束しません。
また,Wの更新式は特に要注意です。なぜなら,Wだけ他のパラメータとは異なり,逆行列の更新式が定義されているからです。更新式に「la.inv」をとったものが,更新後のWになるので気をつけてください。
混合ガウス分布の計算
def calc(self, x, mu, sigma_inv, sigma_det):
exp = -0.5*(x - mu).T@sigma_inv.T@(x - mu)
denomin = np.sqrt(sigma_det)*(np.sqrt(2*np.pi)**self.D)
return np.exp(exp)/denomin
def gauss(self, X, mu, sigma):
output = np.array([])
eps = np.spacing(1)
Eps = eps*np.eye(sigma.shape[0])
sigma_inv = la.inv(sigma)
sigma_det = la.det(sigma)
for i in range(self.N):
output = np.append(output, self.calc(X[i], mu, sigma_inv, sigma_det))
return output
def mix_gauss(self, X, Mu, Sigma, Pi):
output = np.array([Pi[i]*self.gauss(X, Mu[i], Sigma[i]) for i in range(self.K)])
return output, np.sum(output, 0)[None,:]これは,EMアルゴリズムで用いたコードと同じです。各データ点ごとに多変量ガウス分布を計算(calc)して,それらをデータ全体に拡張(gauss)します。それを,混合係数で重み付けして返します(mix_gauss)。
対数尤度の計算
def log_likelihood(self, X, pi):
for i in range(self.K):
self.Sigma[i] = la.inv(self.nu[i] * self.W[i])
self.Mu = self.m
_, out_sum = self.mix_gauss(X, self.Mu, self.Sigma, pi)
logs = np.array([np.log(out_sum[0][n]) for n in range(self.N)])
return np.sum(logs)これも,EMアルゴリズムで用いた関数と同じです。ただ一点,MuとSigmaはガウスウィシャートの期待値で設定しています。ここが,変分ベイズがEMアルゴリズムと大きく異なる点です。
EMアルゴリズムでは,MuとSigmaが直接更新されましたね。変分ベイズでは,それらに分布を仮定したため,その分布から実際の値を取ってくる必要があるのです。どのように取ってくるかは「最大値をとる値」「中央値」等,様々考えられますが,今回は単純に期待値を採用することにしました。式(54)と式(56)です。
VBの実行メソッド
def fit(self, X, iter_max, thr):
self.init_params(X)
log_list = np.array([])
pi = np.array([1/self.K for i in range(self.K)])
log_list = np.append(log_list, self.log_likelihood(X, pi))
count = 0
for i in range(iter_max):
r = self.e_step(X)
pi = self.m_step(X, r)
log_list = np.append(log_list, self.log_likelihood(X, pi))
if np.abs(log_list[count] - log_list[count+1]) < thr:
return count+1, log_list, r, pi, self.Mu, self.Sigma
else:
print("Previous log-likelihood gap:" + str(np.abs(log_list[count] - log_list[count+1])))
count += 1今まで定義してきたメソッドを駆使して,VBの実行メソドを定義します。初期化,Eステップ,Mステップ,収束判定と繰り返すことで,パラメータを更新していきます。収束判定では,「閾値」もしくは「最大更新回数」のいずれかが引っかかった場合に更新をストップするようにしています。
クラス分類
def classify(self, X):
return np.argmax(self.e_step(X), 1) Eステップで計算された負担率の最大値を見ることで,そのデータが属するクラスを判別します。
実行
model = VBGMM(K=4, alpha0=0.01)
n_iter, log_list, r, pi, Mu, Sigma = model.fit(l, iter_max=100, thr = 0.01)
labels = model.classify(l)
print(n_iter)
print(log_list)さて,上で定義したクラスを利用して,modelインスタンスを生成しましょう。とりあえず,クラスタの個数は4,ディリクレ分布ハイパーパラメータの初期値は0.01としました。また,最大更新回数は100回で,閾値は0.01としました。以下のような出力が得られるはずです。
Out:
Previous log-likelihood gap:352374.7690722999
Previous log-likelihood gap:2068.3469153671103
Previous log-likelihood gap:645.1411503082345
Previous log-likelihood gap:305.0644913427459
Previous log-likelihood gap:234.10144599397609
Previous log-likelihood gap:315.719198657207
Previous log-likelihood gap:132.44763434375636
Previous log-likelihood gap:4.526144501374802
Previous log-likelihood gap:0.08259978266869439
10
[-412713.06303586 -60338.29396356 -58269.94704819 -57624.80589788
-57319.74140654 -57085.63996054 -56769.92076189 -56637.47312754
-56632.94698304 -56632.86438326 -56632.86105805]EMと同じくらいの対数尤度でしっかりと収束してくれました。更新回数も10回で,EMとほぼ変わりありません。
視覚化
cm = plt.get_cmap("tab10")
fig = plt.figure()
ax = Axes3D(fig)
N = l.shape[0]
for n in range(N):
ax.plot([l[n][0]], [l[n][1]], [l[n][2]], "o", color=cm(labels[n]), ms=1.5)
ax.view_init(elev=30, azim=45)
plt.show()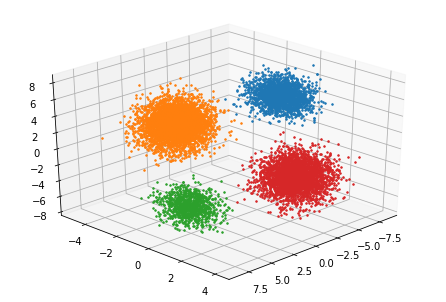 k=4
k=4視覚化の結果,しっかりとクラスタリング出来ていることが分かります。
EMアルゴリズムとの比較実験
PRML10章でも言及がある通り,変分ベイズ(VB)のほうが使うメリットが大きいということです。上でもお伝えしましたが,その理由の1つに,クラスタがスパース化されるという効力が挙げられます。
EMアルゴリズムでは,多くの試行の結果から,クラスタの個数は4が適切だと判断できました。一方,変分ベイズでは,クラスタの個数を大きめ(K=10など)に設定すれば,勝手に適切なクラスタ数にフィットしてくれるというのです。
上でもお伝えしましたが,この働きを「関連度自動決定」と呼びます。不要なゴミは,勝手に小さくなってくれるのが変分ベイズの嬉しいポイントです。試しに,K=8で実験してみましょう。
EMアルゴリズムを用いた場合
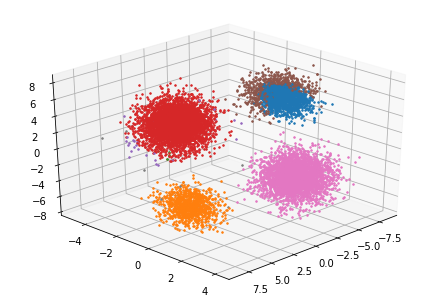 k=8
k=8●更新回数:100回
●最終対数尤度:-56596
やはり,EMアルゴリズムでは,正しくクラスタリングされませんでした。また,閾値を0.01に設定した場合,100回更新しても対数尤度の変化は閾値を下回りませんでした。
変分ベイズを用いた場合
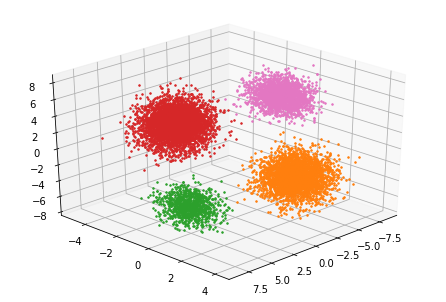 k=8
k=8●更新回数:16回
●最終対数尤度:-56632
一方,変分ベイズを利用した場合では,正しくクラスタリングされ,更新回数も16回でできました。
まとめ
EMアルゴリズムとの比較を通しながら,変分ベイズ法について出来るだけ噛み砕いた説明を心がけました。特に,最尤推定やMAP推定とベイズ推論の違いを頭に置いておくことで,多くの手法をかなり高い立場から俯瞰できるようになると思います。関連度自動決定についても,興味がある方は調べてみてください。
全体のコード
import csv
import numpy as np
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
from numpy import linalg as la
from scipy.special import digamma, gamma, logsumexp
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys
txt_dir = "data.csv"
with open(txt_dir) as f:
reader = csv.reader(f)
l = [row for row in reader]
for i in range(len(l)):
for j in range(len(l[i])):
l[i][j] = float(l[i][j])
l = np.array(l)
class VBGMM():
def __init__(self, K=6, alpha0=0.1):
self.K = K
self.alpha0 = alpha0
def init_params(self, X):
self.N, self.D = X.shape
self.m0 = np.random.randn(self.D)
self.beta0 = np.array([1.0])
self.W0 = np.eye(self.D)
self.nu0 = np.array([self.D])
self.N_k = (self.N / self.K) + np.zeros(self.K)
self.alpha = np.ones(self.K) * self.alpha0
self.beta = np.ones(self.K) * self.beta0
self.m = np.random.randn(self.K, self.D)
self.W = np.tile(self.W0, (self.K, 1, 1))
self.nu = np.ones(self.K)*self.D
self.Sigma = np.zeros((self.K, self.D, self.D))
for k in range(self.K):
self.Sigma[k] = la.inv(self.nu[k] * self.W[k])
self.Mu = self.m
def e_step(self, X):
pi = digamma(self.alpha) - digamma(self.alpha.sum())
Lambda_tilde = np.zeros((self.K))
for k in range(self.K):
digamma_sum = np.array([])
for i in range(self.D):
digamma_sum = np.append(digamma_sum, digamma((self.nu[k] + 1 - i)/2))
A = np.sum(digamma_sum)
B = self.D * np.log(2)
C = np.log(la.det(self.W[k]))
Lambda_tilde[k] = A + B + C
rho = np.zeros((self.N, self.K))
for n in range(self.N):
for k in range(self.K):
gap = (X[n] - self.m[k])[:, None]
A = -(self.D/(2*self.beta[k]))
B = -(self.nu[k]/2)*(gap.T@self.W[k]@gap)
rho[n][k] = pi[k] + 0.5*Lambda_tilde[k] + A + B
r_log = rho - logsumexp(rho, axis=1)[:,None]
r = np.exp(r_log)
r[np.isnan(r)] = 1.0 / (self.K)
return r
def m_step(self, X, r):
self.N_k = np.sum(r, axis=0, keepdims=True).T
barx = (r.T @ X) / self.N_k
S_list = np.zeros((self.N, self.K, self.D, self.D))
for n in range(self.N):
for k in range(self.K):
gap = (X[n] - barx[k])[:, None]
S_list[n][k] = r[n][k] * gap @ gap.T
S = np.sum(S_list, axis=0) / self.N_k[:,None]
self.alpha = self.alpha0 + self.N_k
self.beta = self.beta0 + self.N_k
for k in range(self.K):
self.m[k] = (1/self.beta[k]) * (self.beta0 * self.m0 + self.N_k[k] * barx[k])
for k in range(self.K):
gap = (barx[k] - self.m0)[:, None]
A = la.inv(self.W0)
B = self.N_k[k] * S[k]
C = ((self.beta0*self.N_k[k]) / (self.beta0 + self.N_k[k])) * gap@gap.T
self.W[k] = la.inv(A + B + C)
self.nu[k] = self.nu0 + self.N_k[k]
pi = self.alpha / np.sum(self.alpha, keepdims=True)
return pi
def calc(self, x, mu, sigma_inv, sigma_det):
exp = -0.5*(x - mu).T@sigma_inv.T@(x - mu)
denomin = np.sqrt(sigma_det)*(np.sqrt(2*np.pi)**self.D)
return np.exp(exp)/denomin
def gauss(self, X, mu, sigma):
output = np.array([])
eps = np.spacing(1)
Eps = eps*np.eye(sigma.shape[0])
sigma_inv = la.inv(sigma)
sigma_det = la.det(sigma)
for i in range(self.N):
output = np.append(output, self.calc(X[i], mu, sigma_inv, sigma_det))
return output
def mix_gauss(self, X, Mu, Sigma, Pi):
output = np.array([Pi[i]*self.gauss(X, Mu[i], Sigma[i]) for i in range(self.K)])
return output, np.sum(output, 0)[None,:]
def log_likelihood(self, X, pi):
for i in range(self.K):
self.Sigma[i] = la.inv(self.nu[i] * self.W[i])
self.Mu = self.m
_, out_sum = self.mix_gauss(X, self.Mu, self.Sigma, pi)
logs = np.array([np.log(out_sum[0][n]) for n in range(self.N)])
return np.sum(logs)
def fit(self, X, iter_max, thr):
self.init_params(X)
log_list = np.array([])
pi = np.array([1/self.K for i in range(self.K)])
log_list = np.append(log_list, self.log_likelihood(X, pi))
count = 0
for i in range(iter_max):
r = self.e_step(X)
pi = self.m_step(X, r)
log_list = np.append(log_list, self.log_likelihood(X, pi))
if np.abs(log_list[count] - log_list[count+1]) < thr:
return count+1, log_list, r, pi, self.Mu, self.Sigma
else:
print("Previous log-likelihood gap:" + str(np.abs(log_list[count] - log_list[count+1])))
count += 1
def classify(self, X):
return np.argmax(self.e_step(X), 1)
model = VBGMM(K=8, alpha0=0.01)
n_iter, log_list, r, pi, Mu, Sigma = model.fit(l, iter_max=100, thr = 0.01)
labels = model.classify(l)
print(n_iter)
print(log_list)
cm = plt.get_cmap("tab10")
fig = plt.figure()
ax = Axes3D(fig)
N = l.shape[0]
for n in range(N):
ax.plot([l[n][0]], [l[n][1]], [l[n][2]], "o", color=cm(labels[n]), ms=1.5)
ax.view_init(elev=30, azim=45)
plt.show()
●PRML「パターン認識と機械学習<第10章>」
●http://www.ccn.yamanashi.ac.jp/~tmiyamoto/img/variational_bayes1.pdf



















はじめまして,生物系の院生です!
学部で数学や統計をまともにやっていないので,zukaさんのわかりやすい説明に助けられています!
一点質問です!
式(6)→(7)の式変形なのですが,①KL(q||p)の定義をq(Z)に関する期待値に書き直す②lnの分母分子を入れ替えて正負を逆にする,で合っていますか?
EMアルゴリズムや変分ベイズで行われている,抽象的な式変形にまだ慣れていません…。
教えていただけると助かります!!
ubosus様
図らずもコメントの通知設定がOFFになっており,ご返信が遅れてしまいました。失礼いたしました。(通常であればその日中にご返信できることがほとんどです。)
ここら辺の式変形は,慣れていないと難しく感じますよね。
KLダイバージェンスの定義は$KL[p(x)|q(x)]=\int_{-\infty}^{\infty} p(x)\ln \frac{p(x)}{q(x)}dx=E_{p(x)}[\ln\frac{p(x)}{q(x)}]$ですので,おっしゃっている「①KL(q||p)の定義をq(Z)に関する期待値に書き直す」のみでOKです。
ご返信頂き,ありがとうございます.
式変形を順番に手計算で確かめることでだんだんコツが掴めてきました!
全ての式が理解できるようになるまで頑張ります!
初心者ながら一点気になったのですが,式(8)以降で$E_{q_i(Z_i)}$と$E_{q(Z)}$が区別されていないのが少しわかりにくいと感じました.
ご指摘誠にありがとうございます!修正いたしましたので,ご確認ください.
これ以降も疑問点がありましたら,お気軽にお尋ねください.助かりました!
度々すみません。
変分ベイズに使われる多くのライブラリで,SgdやAdamといった最適化アルゴリズムが使われている理由がいまいち掴めません。
本来,本記事のようにモデル毎に更新式を導出しなければならないところを,最適化アルゴリズムによってパラメータの更新を一般化しているのでしょうか?
ubosus様
ご質問ありがとうございます。
変分法では,解析的に最適解を求められないことがほとんどです。
その場合は,SGDやAdamなどの近似手法に頼るほかないのが現状です。
一般化,というよりかはライブラリとして汎用性を持たせるための苦肉の策というイメージでしょうか。
(例えば,NMFでは解析的に解を求めることができるため,わざわざAdamなどを利用する必要はありませんよね!)
ご返信ありがとうございます!
なるほど…。
“変分法入門”のような変分法の紹介では,分かりやすさを重視するため,解析的に解を求められる特殊な例を用いているんですね。
実験データの解釈のために,データ解析の実用的な部分から学び始めてしまったみたいなので,参考書をもとに基礎から固めようと思います。
はい!
ぜひ,またご指摘・ご質問お願い致します。
とてもわかりやすくて大変助かりました。1つ質問をさせてください。
今回は混合ガウスモデルへの適用ということで解析的に求解が可能な場合を扱っていますが、そうでない場合にはどのような操作を行なっているのでしょうか?
同時分布Pが複雑な関数形をしている状況でどのようにlogPの期待値計算を行なっているのか教えてください。
わた様
ご質問ありがとうございます。質問にお答えしていきます。
>今回は混合ガウスモデルへの適用ということで解析的に求解が可能な場合を扱っていますが、そうでない場合にはどのような操作を行なっているのでしょうか?
非常に本質を突く質問ですね…。変分推論で大切な式(18)が計算できるようにモデルを構築するというのが答えになると思います。式(18)は,期待値計算の積分ができるようにモデルを組み立てなければ,近似すらできないということを示しているとも捉えられます。堂々巡りですが。
>同時分布Pが複雑な関数形をしている状況でどのようにlogPの期待値計算を行なっているのか教えてください。
上述の通り,$\log P$の期待値計算ができるようなモデリングをするということになると思います。期待値が計算できなければ,変分推論を使った近似は計算できません(もし方法があればどなたかご教授ください)。管理人の現時点での解釈としては,変分推論は森羅万象すべての確率分布を近似できるという手法ではないということです。
もしご興味があるのであれば,同様の手法でMCMCなどのサンプリング手法があります。そちらと対比して捉えると,また違った視点から変分推論を理解することができるかと思います。
丁寧な回答ありがとうございます。
>変分推論で大切な式(18)が計算できるようにモデルを構築する
なるほど。自分の中で変分ベイズ はとても汎用的な手法だと勝手に思っていたのですが案外そういうわけでもなさそうですね。
>もしご興味があるのであれば,同様の手法でMCMCなどのサンプリング手法があります。そちらと対比して捉えると,また違った視点から変分推論を理解することができるかと思います。
MCMCについての基本的なことは勉強したのですが、
・式(18)に対して、うまくPが設計できる
(計算効率重視)→変分ベイズ
(精度重視)→MCMC
・式(18)に対して、うまくPが設計できない→MCMC
といった認識で合っているでしょうか?
度々すみません。
わた様
はい。私もおっしゃる通りの認識です。
これから勉強を続けていく中で気づくこともあると思いますので,その際は改めてまとめさせていただきます。
(わた様も何か発見したことがあれば教えていただけますと非常に助かります><)
大変ご丁寧な解説をありがとうございます。
大学院の授業でPRMLの上を輪読しましいたが、
難しかったので助かります。
サイト内にご記載があれば申し訳ないのですが、
上記の data.csv はどのようなデータでしょうか?
また、どこかでダウンロードできますでしょうか?
大変ご丁寧な解説をありがとうございます。
サイト内でご記載があれば、申し訳ないのですが、
上記の data.csv をダウンロードすることはできます
でしょうか?
yaga様
ご連絡ありがとうございます。zukaです。
data.csvは4つのクラスタを適当に作ったものですが,諸事情でローデータをお渡しすることは難しいです><。 何卒,ご理解いただけますと幸いです。 もしよろしければ,例えば2つのクラスタでも十分機能すると思いますので,適当に多峰ガウス分布からサンプリングして偽クラスタを作って試してみると面白いかもしれません。
zuka様
非常にご丁寧なご返信ありがとうございます。
また、重複して質問が投稿されてしまったようで、
申し訳ございませんでした。
ご回答の件、了解いたしました。
自分の研究で、あるデータのクラスタリングを模索しており、
zuka様のコードで動くか試してみたいと思っておりました。
そこで、data.csvの構造と申しますか、形状を知りたかった
のです。
とはいえ、いただいたアドバイス通りに試してみたいと思います。この度はありがとうございました。
yaga様
ご返信ありがとうございます。zukaです。
なるほどです。クラスタリングの利用を検討されているのですか。
最近であれば,DNNベースのクラスタリング手法が主流のようですね。
data.csvの一部の様式を本文中に画像として挿入しました。
ぜひご参照ください。
正直,本記事の実装部分はコメントもなく,コーディングもかなり未熟な部分が多いと思っています。
ですので,時間がある際にリファクタリング含めて新しいブログに移行させようと思っています。
新ブログの体裁と記事が完成し次第,弊サイトにて完成の旨を報告させていただきます。
参考にしていただいて,嬉しい限りです。
これからもどうぞよろしくお願いいたします。
zuka様
ご丁寧なご対応ありがとうございました。
もちろん、DNNで行きたいのですが、
教師データを与えることも考慮して、
様々なクラスタリング手法を模索しています…
k-means++ は微妙な感じです…
私自身、数学もPythonも勉強不足で、zuka様のおっしゃる
未熟な部分がわからないのですが、新ブログを楽しみに
しております!
また、私の研究で、クラスタリングの結果が出れば、
コードが大丈夫かどうか、PRMLの授業の教授に確認
をとることもできるかもしれませんが、
私の研究の発表範囲はおそらく学内に留まりますし、
zuka様に無断で論文本文や参考文献に記載することは
断じて致しませんのでご安心いただければと存じます。
yaga様
はい。ぜひ一緒に頑張っていきましょう^^
変分ベイズ法を用いた混合ガウス分布への適応と実装をありがとうございます!!類を見ない貴重な資料だと思います。理解できるように繰り返し、読ませていただきます。ぜひ混合ベルヌーイ分布への適応と実装についてもご教示いただけないでしょうか?
KFurudate様
コメントありがとうございます!
実装はコメントも付いておらずかなり不親切な内容となっているため,近々アップデート予定です.
混合ベルヌーイ分布のリクエストもありがとうございます.前向きに検討していきます.
ただいま,本サイトを解体して4つの新しいサイトにリニューアルしようと画策中です.
リニューアル後は,より分かりやすさを重視した内容を心がけ,実装も丁寧に行おうと思っています.
その際に,混合ベルヌーイ分布バージョンも作成できたらと思っております.
ご検討ありがとうございます!!
4つの新しいサイトにリニューアルされるのですね!さらにわかりやすくなるなんですごいです。ますますのご活躍を心からお祈りいたします!
いつも拝見させていただいています。
いつも見させていただいています。
質問なのですが、潜在変数に関する最適化の、正規化定数Aを求める際の式変形がど
のようになっているかわかりません。
もしよろしければ教えていただきたいです。
VB様
ご連絡ありがとうございます。
ご返信が遅くなってしまい,大変失礼いたしました。
また,mathjaxのバージョンが更新されたためか,式番号が抜けてしまっていますね。後ほど修正します。
Aは$q^{\ast}(\bf{Z})$が足して1になるための正規化定数でした。
\begin{align}
A &= \sum_{Z} \prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{n k}^{z_{n k}}
\end{align}
$z$がone-hot vectorであることに注意すると,以下のように変形できます。
\begin{align}
\begin{array}{l}
\sum_{Z} \prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{n k}^{z_{n k}} &=\sum_{z_{1}} \prod_{k=1}^{K} \rho_{1 k}^{z_{1 k}} \cdot \sum_{z_{2}} \prod_{k=1}^{K} \rho_{2 k}^{z_{2 k}} \cdots \\
&=\sum_{k} \rho_{1 k} \cdot \sum_{k} \rho_{2 k} \cdots \\
&=\prod_{n=1}^{N} \sum_{k=1}^{K} \rho_{n k}
\end{array}
\end{align}
いかがでしょうか?
いつも楽しく拝見しております。
こちらの記事を読んでいて「あれっ?」と思うことがありましたので、記載致します。
(78)式の第一項で$E[\ln\pi_k]$を計算していますが、
$q(\pi)$がディレクレ分布であることを示しているのは(101)-(103)式であり、(78)式より後ろの方で示していたので
$q(\pi)$がディレクレ分布であることを示してから、期待値を計算したほうがいいんじゃないかって思いました。
maki 様
ご返信遅れてしまい大変申し訳ありません。
本記事の内容を洗練させて新しいブログの方に移植致しました。
ご指摘の内容も反映されているはずです。
ぜひ参考にしていただけますと幸いです。
https://academ-aid.com/variational-bayes