本記事の内容は新ブログに移行されました。
こちらのブログにコメントをいただいても
ご返信が遅れてしまう場合がございます。
予めご了承ください。
ご質問やフィードバックは
上記サイトへお願い致します。
今回は，確率モデルの最尤解を求めるための繰り返し近似法であるEM(Expectation–Maximization)アルゴリズムの解説とPythonで実装する方法をお伝えしていこうと思います。
本記事はpython実践講座シリーズの内容になります。その他の記事は，こちらの「Python入門講座/実践講座まとめ」をご覧ください。また，本記事の実装はPRML「パターン認識と機械学習＜第９章＞」に基づいています。演習問題は当サイトにて簡単に解答を載せていますので，参考にしていただければと思います。
読みたい場所へジャンプ！
EMの気持ち
機械学習を学ばれている方であれば，EMアルゴリズムが一番最初に大きく立ちはだかる壁だとも言えます。何をしたいのか，そもそも何のための手法なのかが見えなくなってしまう場合が多いと思います。
そこで，今回は実装の前に，簡単にEMアルゴリズムの気持ちをお伝えしてから，ザッと数学的な背景をおさらいして，最後に実装を載せていきたいと思います。早速ですが，一問一答形式でEMアルゴリズムに関してみていきたいと思います。
疑問１：何のための手法なの？
EMアルゴリズムは，確率モデルのパラメータに関する最尤解を求めるための手法です。噛み砕いていきましょう。確率モデルというのは，簡単に言えば「現象の裏側に何か適当な分布を仮定すること」です。
しかし，適当な分布を仮定したところで，その分布の形状を決定するパラメータを定めなくては，現象を確率モデルで説明することはできません。そこで，得られた情報（現象）に尤も良くフィットするようなパラメータを求める操作が「最尤推定」なのです。
ちなみに，こちらの記事（【初学者向き】ベイズ推論とは？事前分布や事後分布をド素人向けに分かりやすく解説してみます！）では，尤度，事前分布，事後分布等のベイズ推論に登場する用語を簡単に説明していますので，ぜひ参考にして見てください。
もう少し詳しく説明すると，EMアルゴリズムは潜在変数をもつ確率モデルの最尤解を求める手法です。しかし，多くのモデルの場合，対数尤度関数を計算すると「log-sum」が出現してしまいます。
そのため，潜在変数を含むモデルの最尤解を解析的に求めることは難しくなっているのです。EMアルゴリズムでは，この問題を「下界を最大化していく」ことで解決していきます。
疑問２：EMってどういう意味？
EMアルゴリズムのEMは「Expectation–Maximization」の頭文字を取ったものです。日本語訳すると「期待値化・最大化アルゴリズム」といったところでしょうか。
実は，あとで説明するように，EMアルゴリズムは二つのステップを繰り返します。それぞれのステップは「Eステップ」「Mステップ」と呼ばれていて，それぞれ「期待値を取る」「偏微分をして最尤解を求める」という操作に相当しています。
つまり，EMアルゴリズムのEMというのは，近似手法の各ステップの操作を表しているのです。
疑問３：K-meansとの関わりは？
EMアルゴリズムを学んでいると，必ずと言っていいほど出てくる話題がK-meansとの関連性です。実は，K-meansは混合ガウス分布に関するEMアルゴリズムの分散を0に近づけたときの極限として与えられます。
K-meansは，あるデータ点がどこのクラスタに属するかを「ハード」に割り当てます。例えば，４番目のデータ点は２個目のクラスタに属する，といった具合にです。
一方，混合ガウス分布に基づくクラスタリングでは，$n$番目のデータが$k$番目のクラスタに属する割合を$\gamma_{nk}$で表します。例えば，$\gamma_{42}=0.3$であれば，４番目のデータ点が2番目のクラスタに属する割合は0.3というようになります。このようにクラスタリングすることを，「ソフト」な割り当てを行う，と言います。
ソフトからハードな割り当てにするためには，ガウス分布において分散（共分散行列の対角成分）を0に近づければOKということです。
疑問５：下界ってなに？
対数尤度関数を２つの項に分解したときの片っぽうです。ちなみに，もう一方はKLダイバージェンスです。KLダイバージェンスが非負値なために，対数尤度関数が下回らない下限として「下界」と呼ばれています。Mステップでは，パラメータに関して下界を最大化します。
疑問４：Q関数ってなに？
一般化EMアルゴリズムの導出で出てくるのが，Q関数です。結論から言うと，Q関数は「尤度関数の潜在変数に関する期待値」のことです。何のことだかサッパリだと思います。
数学的な背景は後ほど説明するとして，とりあえずの解釈をお伝えしておくと，下界をパラメータに関して整理しただけの式のことです。logの性質を利用して下界を和になおしたときに，パラメータに依存しない部分を除けばQ関数の出来上がりです。
疑問５：一般化アルゴリズムのEステップでは事後確率を求めるのになぜ「E」ステップと呼ばれているの？
クリティカルな疑問だと思います。後ほど説明するように，一般化EMアルゴリズムの説明では，Eステップでは潜在変数の事後確率を求めます。しかし，Eステップでは「期待値」を求めるはずでしたよね…？
ここでは，私の見解をお伝えしようと思います。Eステップでは，潜在変数の事後確率を計算しますが，この理由は「Mステップの目的関数であるQ関数を計算するのに必要だから」です。
そして，Q関数自体が期待値を取る操作に相当していましたよね。つまり，Q関数値という「期待値」を計算するために必要な事後確率をEステップでは計算しているのです。また，注意が必要なのですが，混合ガウス分布のEステップでは事後確率を求めるのではなくて，負担率（事後確率に関する潜在変数の期待値）を計算します。
実はこの計算は，事後確率を求める操作と本質的には同じです。なぜなら，混合ガウス分布のEステップで負担率を求める理由は，Mステップで求める最尤解を計算するのに必要だからです。
疑問６：K（クラスタの個数）はどうやって決めるの？
EMアルゴリズムでは，クラスタリングするクラスの個数は自分で決めなくてはなりません。ここが，問題点とも言えるでしょう。ちなみに，EMアルゴリズムをベイズ的に拡張した「変分ベイズ法」では，この問題点をエレガントに解決してくれます。
疑問７：EMの解は必ず正しいの？
実は，EMアルゴリズムで導出される最尤解は，局所解の可能性があります。そのため，初期値をうまく与えてあげる必要があります。たとえば，初期値としてクラスタの平均値は標準正規分布から生成し，共分散行列は単位行列として設定するとよいでしょう。
疑問８：潜在変数の事後確率って計算できるの？
Eステップでは，潜在変数の事後確率を計算することになりますが，この計算って実際に行えるのでしょうか。これは，行えます。なぜなら，まず第一に仮定している確率モデルを利用することができるからです。例えば，ガウス分布やポアソン分布を仮定していれば，式を知っていますから，計算することができますね。
また，事後分布ですから，パラメータは既知であるという条件です。つまり，潜在変数以外の値は分かっている状態ですので，分布の式に当てはめることで事後確率を計算することができます。
EMアルゴリズム
まずは，一般のEMアルゴリズムについて確認していったうえで，混合ガウス分布に適用していくという流れにしましょう。さて，以下では数式を用いていきます。私たちが最大化したい関数は，$\ln p(\boldsymbol{X}|\boldsymbol{\theta})$でした。潜在変数$\boldsymbol{Z}$を噛ませることで，以下のように分解することができます。
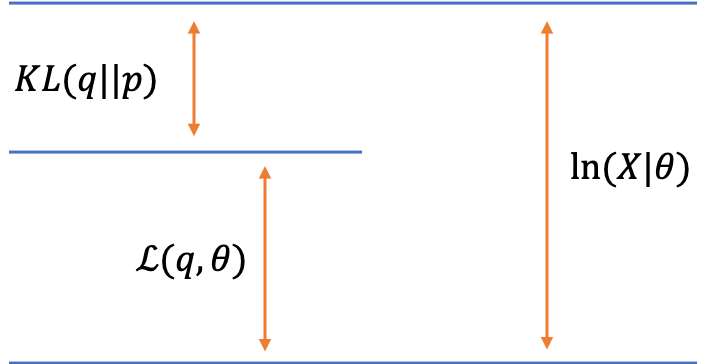対数尤度関数の２つの分解\begin{eqnarray}
\ln p(\boldsymbol{X}|\boldsymbol{\theta}) = \mathcal{L}(q, \boldsymbol{\theta}) + KL(q\|p)
\end{eqnarray}
第一項目は下界と呼ばれており，第二項目はKLダイバージェンスを表しています。それぞれの定義は以下の通りです。
\begin{eqnarray}
\mathcal{L}(q, \boldsymbol{\theta}) &=& \sum_{\boldsymbol{Z}}q(\boldsymbol{Z})\ln \{ \frac{p(\boldsymbol{X}, \boldsymbol{Z} | \boldsymbol{\theta})}{q(\boldsymbol{Z})} \} \\
KL(q \| p) &=& \sum_{\boldsymbol{Z}} q(\boldsymbol{Z}) \ln \{ \frac{q(\boldsymbol{Z})}{p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{\theta})} \}
\end{eqnarray}
ちなみに，式（1）の導出には２つの方法があります。１つは，対数尤度関数にイェンゼンの不等式を利用して下界を導出する方法です。これによれば，対数尤度関数は下界によって下からおさえられます。また，その差は$q$と$p$のKLダイバージェンスになります。
２つ目の方法は，式（2）と式（3）を足すことで対数尤度関数になることを確認する方法です。これは，かなり天下り的な発想ですが，確認できることに変わりはありません。
さて，この２つの分解を利用して，対数尤度関数を最大化していきましょう。最適化するパラメータの対象は，$\theta$と$q$です。高校数学でも習ったように，$\theta$と$q$をそれぞれ固定しながらその和を最大化していくという方法をとりましょう。
それでは，下界とKLダイバージェンスはどちらから注目していけばいいのでしょうか。それは，どちらでもOKです。Eステップから始めるか，Mステップから始めるかは，初期値の設定の違いだけです。ここでは，「EM」アルゴリズムと呼ばれていることから，とりあえずEステップと呼ばれるフェーズから考えていきます。Eステップでは，「$\theta$を固定してKLダイバージェンスを最小化する$q$を求める」操作をします。
しかし，一点注意点があります。感覚的には「KLダイベージェンスを最大化する$q$」を求めたくなりますが，実はこれが反対で，KLダイバージェンスを最小化する$q$を求めることになります。理由は，KLダイバージェンスを最小化することで，下界が最大化されるからです。
このポイントを理解するためには，固定されている変数に注意する必要があります。今回は$\theta$を固定しているため，$\ln p(\boldsymbol{X}|\boldsymbol{\theta})$も固定されます。つまり，和の結果が固定されているため，一方（KLダイバージェンス）が最小化されれば，もう一方（下界）は最大化されるということなのです。
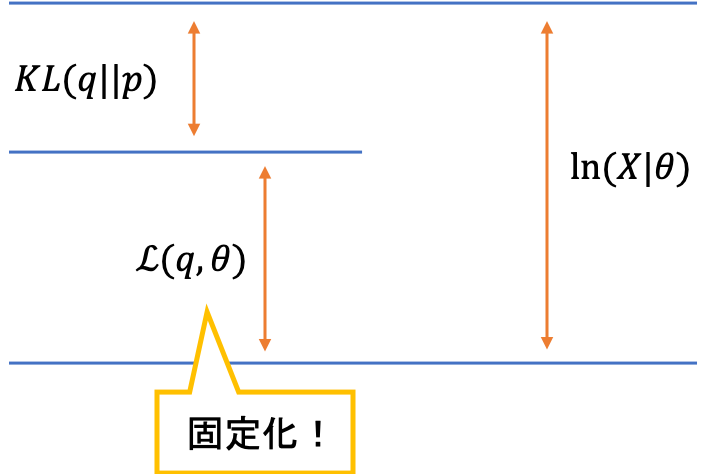qに関する固定化こちらの考え方は簡単で，KLダイバージェンスが最小となるのは，KLダイバージェンスが0となるとき，つまり$q=p$のときです。これを数式で表してみましょう。
\begin{eqnarray}
\arg \min_q (KL(q|p)) &=& p \\
&=& p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{\theta})
\end{eqnarray}
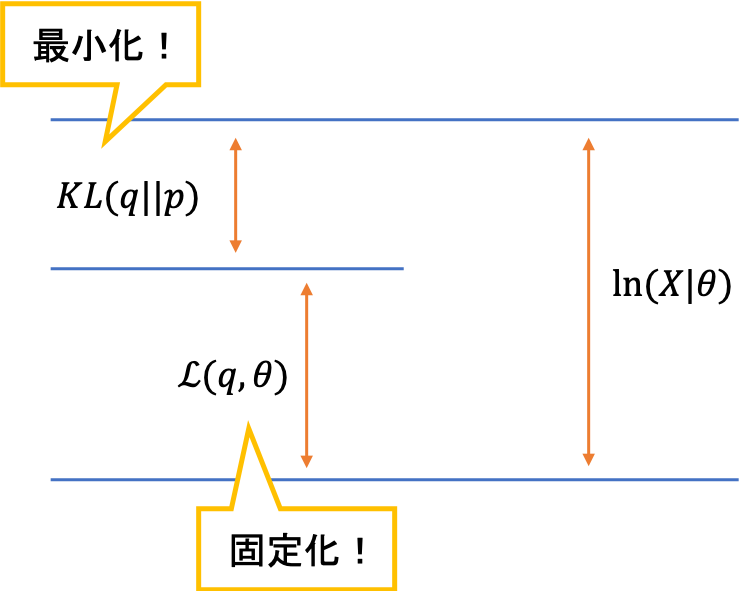まずはKLダイバージェンスから注目しますこの操作が，EMアルゴリズムのEステップに相当します。つまり，$\theta$を固定してKLダイバージェンスを最小化する$q$を求めるということです。このとき，固定化されている下界も$\theta$が変化するために変化します。（先ほどの和の議論と同じ）
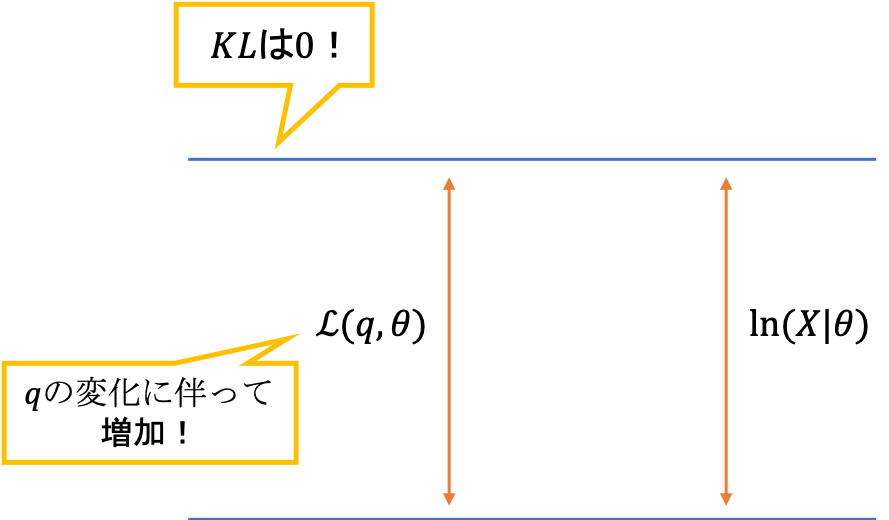qに関する固定化なのでθを動かせば下界は可変続くMステップでは，下界をパラメータに関して最大化します。これは，対数尤度関数を底上げしているイメージで，実際に対数尤度関数は$q$には依存せず$\theta$に依存しているため，このMステップで増加していくことになります。
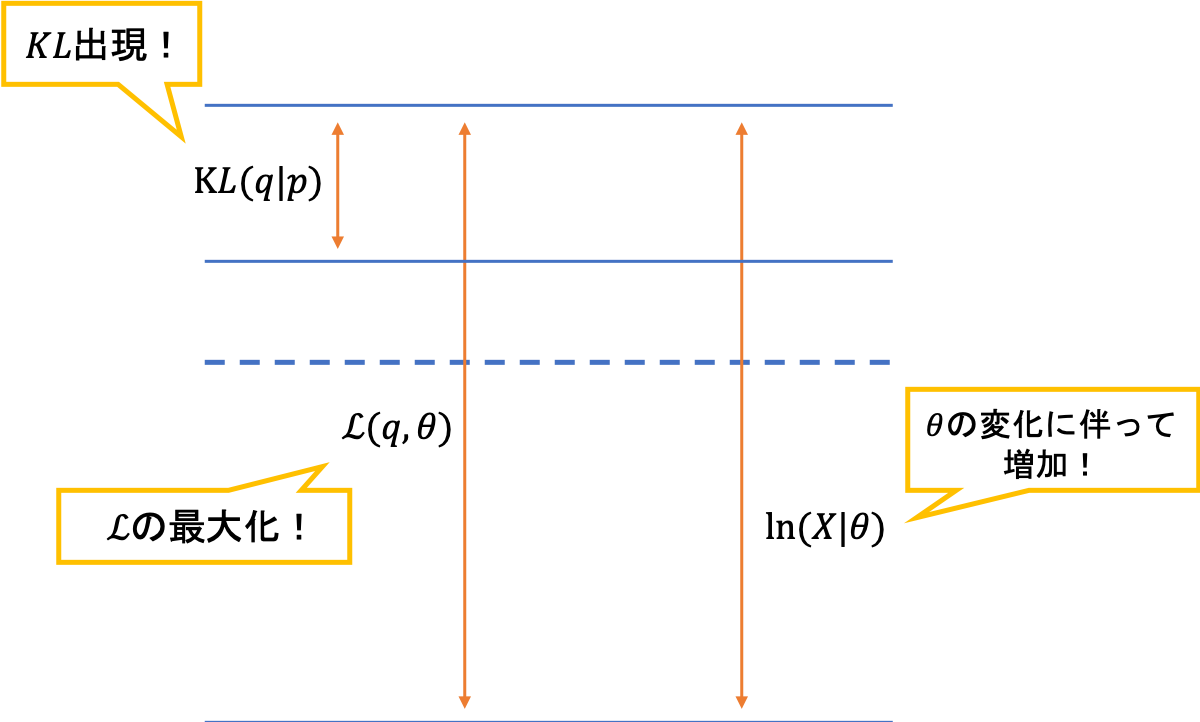今度は下界を最大化します実際に，数式で確認していきましょう。まずは，下界の定義から和に分解します。$\theta$に関係しない項は定数項にしてしまいます。
\begin{eqnarray}
\mathcal{L}(q, \boldsymbol{\theta}) &=& \sum_{\boldsymbol{Z}}q(\boldsymbol{Z})\ln \{ \frac{p(\boldsymbol{X}, \boldsymbol{Z} | \boldsymbol{\theta})}{q(\boldsymbol{Z})} \} \\
&=& \sum_{\boldsymbol{Z}}q(\boldsymbol{Z})\ln p(\boldsymbol{X}, \boldsymbol{Z} | \boldsymbol{\theta}) – \sum_{\boldsymbol{Z}}q(\boldsymbol{Z})\ln q(\boldsymbol{Z}) \\
&=& \sum_{\boldsymbol{Z}}q(\boldsymbol{Z})\ln p(\boldsymbol{X}, \boldsymbol{Z} | \boldsymbol{\theta}) + const
\end{eqnarray}
ここで，Eステップの結果を思い出してみましょう。上の式では，まだKLダイバージェンスを0にした結果が反映されていませんね。そこで，Eステップの解である$q = p$，つまり$q(\boldsymbol{Z}) = p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{\theta})$を代入してみましょう。ここでは，更新されていない$\theta$は$\theta^{old}$と書くことにします。つまり，$q(\boldsymbol{Z}) = p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{\theta^{old}})$を代入することになります。
\begin{eqnarray}
\mathcal{L}(q, \boldsymbol{\theta}) &=& \sum_{\boldsymbol{Z}}q(\boldsymbol{Z})\ln p(\boldsymbol{X}, \boldsymbol{Z} | \boldsymbol{\theta}) + const \\
&=& \sum_{\boldsymbol{Z}}p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{\theta^{old}})\ln p(\boldsymbol{X}, \boldsymbol{Z} | \boldsymbol{\theta}) + const
\end{eqnarray}
はい，出ました！これが噂のQ関数です。数式で表します。
\begin{eqnarray}
\mathcal{L}(q, \boldsymbol{\theta}) &=& \sum_{\boldsymbol{Z}}p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{\theta^{old}})\ln p(\boldsymbol{X}, \boldsymbol{Z} | \boldsymbol{\theta}) + const \\
&=& Q(\boldsymbol{\theta}, \boldsymbol{\theta}^{old}) + const
\end{eqnarray}
上でもお伝えした通り，Q関数はしっかりと「尤度関数の潜在変数に関する期待値」となっていますね。さて，一般化EMアルゴリズムをまとめておきましょう。
１．パラメータを初期化
２．Eステップ
→潜在変数の事後確率を計算
３．Mステップ
→下界を最適化
混合ガウス分布とEMアルゴリズム
さて，本題に入っていきたいと思います。今回は，EMアルゴリズムを適用する具体例として，混合ガウス分布（GMM）のパラメータ推定を挙げたいと思います。
となると思います。具体的なイメージをしていきましょう。あるデータが与えられます。そのデータを，いくつかのクラスタに分類したいと思っているとします。そのときに，与えられたデータ点は「いくつかのガウス分布から生成されたものだ」と仮定するのが，混合ガウス分布を利用したクラスタリングです。
EMアルゴリズムでは，いくつかの混合ガウス分布のパラメータ（平均，共分散行列，混合係数）を推定するという流れになります。つまり，与えられたデータの生成をよく裏付けられるようないくつかのガウス分布の形状を求めることが，今回のミッションです。
まずは，Eステップからみていきましょう。本来，事後確率を求めるのがEステップでした。しかし，GMMの場合は，「事後確率に関する潜在変数の期待値」を求めるのがEステップに相当します。なぜなら，Eステップで期待値まで計算してしまえば，そのままMステップに利用できるからです。
実際に，数式をみてみましょう。ベイズの定理より，潜在変数の事後確率は以下のように変形できます。
\begin{eqnarray}
p(z_{nk}|\boldsymbol{x}_n, \boldsymbol{\theta})
&=& \frac{p(\boldsymbol{x}_n, z_{nk} | \boldsymbol{\theta})}{p(\boldsymbol{x}_n|\boldsymbol{\theta})} \\
&=& \frac{p(\boldsymbol{x}_n, z_{nk} | \boldsymbol{\theta})}{\sum_{z_n}p(\boldsymbol{x}_n, z_{nj}|\boldsymbol{\theta})} \\
&=& \frac{p(z_{nk})p(\boldsymbol{x}_n | z_{nk},\boldsymbol{\theta})}{\sum_{z_n}p(z_{nj})p(\boldsymbol{x}_n|z_{nj}, \boldsymbol{\theta})}\\
&=& \frac{\{ \pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \}^{z_{nk}}}{\sum_{z_n} \{ \pi_j \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j) \}^{z_{nj}}}
\end{eqnarray}
Eステップでは，この期待値を計算してしまうのでした。実際に，式にしてみましょう。
\begin{eqnarray}
E_{z|x}[z_{nk}]
&=& \sum_{z_n} z_{nk} p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta})\\
&=& \sum_{z_n} z_{nk} \frac{ \{\pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \}^{z_{nk}}}{\sum_{z_n} \{ \pi_j \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j) \}^{z_{nj}}}\\
&=& \frac{\pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)} {\sum_{j}\pi_j \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}
\end{eqnarray}
出てきました。この結果が，負担率と呼ばれるものです。数式では$\gamma(z_{nk})$と定義されます。
\begin{eqnarray}
\frac{\pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)} {\sum_{j}\pi_j \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}&=& \gamma(z_{nk})
\end{eqnarray}
この式の解釈を考えてみましょう。分母は，混合ガウス分布の各クラスタに関する和です。分子は，混合ガウス分布のある特定のクラスタ１つの値です。つまり，負担率とは，あるクラスタ$k$が，データ$\boldsymbol{x}_n$をどれだけよく説明しているかを，全体に占める割合で表したものなのです。
ちなみに，負担率は「$z_{nk}=1$となる事後確率」とも等価です。なぜなら，$\boldsymbol{z}$は二値変数のベクトルであり，事後確率に関する潜在変数の期待値を取れば，$z_{nk}=1$となる事後確率しか残らないからです。しかも，その係数は$z_{nk} = 1$ですので消えてしまい，期待値と事後確率は完全に等価になります。以下に数学的な証明を載せておきます。
\begin{eqnarray}
p(z_{nk}=1|\boldsymbol{x}_n, \boldsymbol{\theta})
&=&\frac{ \pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) }{\sum_{j} \pi_j \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j) }\\
&=& \gamma(z_{nk})
\end{eqnarray}
他にも，以下のようにして「$z_{nk}=1$の事後確率と期待値は等価」を示すことができます。
\begin{eqnarray}
E_{z|x}[z_{nk}]
&=& 1 \cdot p(z_{nk}=1|\boldsymbol{x}_n, \boldsymbol{\theta}) + 0 \cdot p(z_{nk}=0|\boldsymbol{x}_n, \boldsymbol{\theta})\\
&=& p(z_{nk}=1|\boldsymbol{x}_n, \boldsymbol{\theta})\\
&=& \gamma(z_{nk})
\end{eqnarray}
さて，まとめていきます。上述の通り，Eステップでは「事後確率に関する潜在変数の期待値（＝負担率）」を計算するのでした。負担率は，混合ガウス分布の式を使って，割合のような形で定義されていましたね。
負担率を計算する。
\begin{eqnarray}
\gamma(z_{nk}) = \frac{\pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)} {\sum_{j}\pi_j \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}
\end{eqnarray}
さて，次はMステップです。Mステップでは，Q関数を最大化するパラメータを偏微分を利用して求めていきます。このときに注意が必要なのは，パラメータのうち$\pi_k$だけは$\sum_k \pi_k = 1$という制限がありますので，ラグランジュの未定乗数法を利用するということです。
ですので，Q関数を一旦$F$とおき，$F$に$\sum_k \pi_k = 1$の制限をつけたラグランジュ関数を$G$とおくことにします。
\begin{eqnarray}
F &=& E_{Z|X} [ \ln p(\boldsymbol{X},\boldsymbol{Z} | \boldsymbol{\theta} )] \\
&=& E_{Z|X}[\sum_n \sum_k z_{nk}(\ln \pi_k – \ln \mathcal{N}(\boldsymbol{x}_n|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k))] \\
&\overset{\theta}{=}& \sum_n \sum_k E_{Z|X} [z_{nk}] \{ -\frac{1}{2}\ln |\Sigma_k|-\frac{1}{2}(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \Sigma_k^{-1}(\boldsymbol{x}_n – \boldsymbol{\mu}_k) \} \\
&=& \sum_n \sum_k \gamma(z_{nk}) \{ -\frac{1}{2}\ln |\Sigma_k|-\frac{1}{2}(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \Sigma_k^{-1}(\boldsymbol{x}_n – \boldsymbol{\mu}_k) \}\\
G &=& F + \lambda(\sum_k \pi_k – 1)
\end{eqnarray}
それぞれ，実際に計算をしていきましょう。（スクロールできます）
\frac{\partial F}{\partial \boldsymbol{\mu}_k}
&=& \sum_n \gamma(z_{nk}) \cdot \{ -\frac{1}{2}\cdot 2\Sigma_k^{-1} (\boldsymbol{x}_n – \boldsymbol{\mu}_k) \}\\
&=& 0\\
\Leftrightarrow\boldsymbol{\mu}_k &=& \frac{\sum_n \gamma(z_{nk})\boldsymbol{x}_n}{\sum_n \gamma(z_{nk})}\\
&=& \frac{\sum_n \gamma(z_{nk})\boldsymbol{x}_n}{N_k}\\
\\
\\
\frac{\partial F}{\partial \boldsymbol{\Sigma}_k}
&=& \sum_n \gamma(z_{nk}) \cdot \{ -\frac{1}{2} \Sigma_k^{-1} -\frac{1}{2}\frac{\partial}{\partial \Sigma_k}(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T \Sigma_k^{-1}(\boldsymbol{x}_n – \boldsymbol{\mu}_k) \}\\
&=& \sum_n \gamma(z_{nk}) \cdot \{ -\frac{1}{2} \Sigma_k^{-1} -\frac{1}{2} \Sigma_k^{-1} (\boldsymbol{x}_n – \boldsymbol{\mu}_k)(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T\Sigma_k^{-1}\} \tag{※}\\
&=& 0\\
\Leftrightarrow\boldsymbol{\Sigma}_k &=& \frac{\sum_n \gamma(z_{nk}) (\boldsymbol{x}_n – \boldsymbol{\mu}_k)(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T}{\sum_n \gamma(z_{nk})}\\
&=& \frac{\sum_n \gamma(z_{nk}) (\boldsymbol{x}_n – \boldsymbol{\mu}_k)(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T}{N_k}\\
\\
\\
\frac{\partial G}{\partial \pi_k}
&=& \sum_n \gamma(z_{nk})\frac{1}{\pi_k}+\lambda \\
&=& 0\\
\Leftrightarrow \sum_n \gamma(z_{nk}) +\lambda \pi_k &=& 0\\
\Rightarrow \sum_n \sum_k \gamma(z_{nk}) + \lambda &=& 0\\
\Leftrightarrow \lambda &=& – \sum_n \sum_k \gamma(z_{nk})\\
\Rightarrow \pi_k &=& \frac{\sum_n \gamma(z_{nk})}{\sum_n \sum_k \gamma(z_{nk})}\\
&=& \frac{N_k}{N}
\end{eqnarray}
ただし，式変形の途中（※）で以下の公式を利用しました。
\begin{eqnarray}
\frac{\partial a^TX^{-1}b}{\partial X} = – X^{-T} ab^T X^{-T}
\end{eqnarray}
さて，まとめていきましょう。
Q関数を最大化するパラメータを偏微分，もしくはラグランジュの未定乗数法を利用して求める。
\begin{eqnarray}
\boldsymbol{\mu}_k
&=& \frac{\sum_n \gamma(z_{nk})\boldsymbol{x}_n}{N_k}\\
\boldsymbol{\Sigma}_k
&=& \frac{\sum_n \gamma(z_{nk}) (\boldsymbol{x}_n – \boldsymbol{\mu}_k)(\boldsymbol{x}_n – \boldsymbol{\mu}_k)^T}{N_k}\\
\pi_k
&=& \frac{N_k}{N}
\end{eqnarray}
以上で，理論的な背景は終了です。お疲れ様でした。以下では，早速実装を確認していきたいと思います。
実装
最初に細かく関数を見ていって，最後に全体のコードをお伝えしたいと思います。本当であれば，しっかりとクラスを作って見通しの良いコーディングをするべきなのですが，ここでは関数をとりあえず定義していって，それらを組み合わせてEMという関数を作る方針でいきたいと思います。
また，今回は以下のような用法を想定しています。全体のコードを「em.py」として保存し，コマンドライン上で以下のように引数を与えてあげれば，python上のコードでsysが拾ってくれます。負担率とパラメータはファイルに書き出して保存するようにしています。
python em.py [データファイル名] [負担率書き出しファイル名] [パラメータ書き出しファイル名]必要なモジュール等のインポート
import sys
import csv
import numpy as np
from numpy import linalg as la
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D標準的なライブラリ等をインポートしています。データを読み込むためにcsvもインポートしています。laは逆行列や行列式を求めるためにインポートしています。
コマンドラインからの引数を受け取る
txt_dir = sys.argv[1]
csv_name = sys.argv[2]
dat_name = sys.argv[3]用法にも書いた通り，最初の引数はデータファイル名，次の引数は負担率をcsvで保存するためのファイル名，最後の引数はパラメータの値を保存するためのファイル名です。
データファイルを読み込む
with open(txt_dir) as f:
reader = csv.reader(f)
l = [row for row in reader]
for i in range(len(l)):
for j in range(len(l[i])):
l[i][j] = float(l[i][j])
l = np.array(l)csvを読み込んで，numpyのarrayとして定義しておきます。今回は，10000個の３次元データを利用します。また，以下では「（サンプル数）×（次元数）」で保存されているとします。
多次元ガウス分布の出力
def calc(x, mu, sigma_inv, sigma_det):
D = x.shape[0]
exp = -0.5*(x - mu).T @ sigma_inv.T @ (x - mu)
denomin = np.sqrt(sigma_det)*(np.sqrt(2*np.pi)**D)
return np.exp(exp)/denominここでは，ある１点のデータを多次元ガウス分布に突っ込んだときに出される出力を計算しています。ポイントなのですが，ここでは共分散行列の逆行列と行列式を引数として設定しています。この理由は，この関数内で逆行列を行列式を計算してしまうと，10000回も（同じ）その計算を繰り返すことになるからです。
データ全体に対するガウス分布の出力
def gauss(X, mu, sigma):
output = np.array([])
eps = np.spacing(1)
Eps = eps*np.eye(sigma.shape[0])
sigma_inv = la.inv(sigma)
sigma_det = la.det(sigma)
N = X.shape[0]
for i in range(N):
output = np.append(output, calc(X[i], mu, sigma_inv, sigma_det))
return outputここでは，データ全体をガウス分布に突っ込んだ時の出力を行列で返しています。ここで逆行列を行列式を計算することにより，無駄な計算を省くことができます。
混合ガウス分布の計算
def mix_gauss(X, Mu, Sigma, Pi):
k = len(Mu)
output = np.array([Pi[i]*gauss(X, Mu[i], Sigma[i]) for i in range(k)])
return output, np.sum(output, 0)[None,:]上で求めた多次元ガウス分布の出力を，$\pi_k$で重み付けして出力します。出力は，後のために次元を拡張しておきます。
初期値設定
def setInitial(X, k):
D = X.shape[1]
Mu = np.random.randn(k, D)
Sigma = np.array([np.eye(D) for i in range(k)])
Pi = np.array([1/k for i in range(k)])
return Mu, Sigma, Pi平均の初期値は標準正規分布から，共分散の初期値は単位行列，混合係数の初期値はクラス数で等分した確率としています。
対数尤度関数の計算
def log_likelihood(X, Mu, Sigma, Pi):
K = Mu.shape[0]
D = X.shape[1]
N = X.shape[0]
_, out_sum = mix_gauss(X, Mu, Sigma, Pi)
logs = np.array([np.log(out_sum[0][n]) for n in range(N)])
return np.sum(logs)収束判定のために，対数尤度関数を計算する関数を定義しています。対数尤度関数は，混合正規分布のクラス数に関する和の対数を取って，それらのサンプル数に関する和を計算します。
\begin{eqnarray}
\ln p(\boldsymbol{X} | \boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \sum_{k} \pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)
\end{eqnarray}
EMアルゴリズムの更新式
def EM(X, k, Mu, Sigma, Pi, thr):
K = Mu.shape[0]
D = X.shape[1]
N = X.shape[0]
log_list = np.array([])
log_list = np.append(log_list, log_likelihood(X, Mu, Sigma, Pi))
count = 0
while True:
out_com, out_sum = mix_gauss(X, Mu, Sigma, Pi)
gamma = out_com / out_sum
N_k = np.sum(gamma, 1)[:,None]
Mu = (gamma @ X) / N_k
sigma_list = np.zeros((N, K, D, D))
for k in range(K):
for n in range(N):
sigma_com = gamma[k][n]*(X[n] - Mu[k])[:,None]@((X[n] - Mu[k]))[None,:]
sigma_list[n][k] = sigma_com
Sigma = np.sum(sigma_list, 0) / N_k[:,None]
Pi = N_k/N
log_list = np.append(log_list, log_likelihood(X, Mu, Sigma, Pi))
if np.abs(log_list[count] - log_list[count+1]) < thr:
return count+1, log_list, Mu, Sigma, Pi, gamma
else:
print("Previous log-likelihood gap:" + str(np.abs(log_list[count] - log_list[count+1])))
count += 1閾値を設定して，対数尤度関数の変化分がその閾値を下回ったときに繰り返しを終了するように設定しています。更新式は，上でお伝えした通りです。
アルゴリズムの実行
thr = 0.01
k = 4
Mu, Sigma, Pi = setInitial(l, k)
n_iter, log_list, Mu, Sigma, Pi, gamma = EM(l, k, Mu, Sigma, Pi, thr)
print("Iteration:"+str(n_iter))
print("log-likelihood:"+str(log_list))実際に，上で定義したEMアルゴリズムを実行しています。ここでは，何回目の繰り返しなのか，対数尤度関数の値はいくらなのかを表示するようにしています。閾値は，適当に0.01としました。np.allcloseを利用しても良いかもしれません。また，クラスタの個数は何回か試したところ４個がよさそうでしたので，あらかじめ定めてしまいました。
局所解に陥らなければ，出力はおおよそ以下のようになります。
Output:
Previous log-likelihood gap:110537.84635013063
Previous log-likelihood gap:1692.5207489158565
Previous log-likelihood gap:625.8344688315847
Previous log-likelihood gap:409.1997838134703
Previous log-likelihood gap:17.39281884128286
Previous log-likelihood gap:0.07082455944328103
Iteration:7
log-likelihood:[-169914.59718808 -59376.75083795 -57684.23008903 -57058.3956202
-56649.19583639 -56631.80301754 -56631.73219298 -56631.73176504]出力する変数の定義
params = np.array([Mu.ravel(), Sigma.ravel(), Pi.ravel()])今回は，負担率とパラメータを出力するのでした。負担率はすでにまとまった配列として定義されているため，今回新しくパラメータをまとめて配列化しておきます。その際，ravel()で一次元化しておかなければ，ファイルとして出力する際にエラーを起こしてしまいます。
属するクラスターの判別
index = np.argmax(gamma, 0)負担率の大きさから，データ点が属するクラスタを判別しています。クラスタとは，どの正規分布から生成したものとみなせるかを表しているものです。
可視化
cm = plt.get_cmap("tab10")
fig = plt.figure()
ax = Axes3D(fig)
N = l.shape[0]
for n in range(N):
ax.plot([l[n][0]], [l[n][1]], [l[n][2]], "o", color=cm(index[n]), ms=1.5)
ax.view_init(elev=30, azim=45)
plt.show()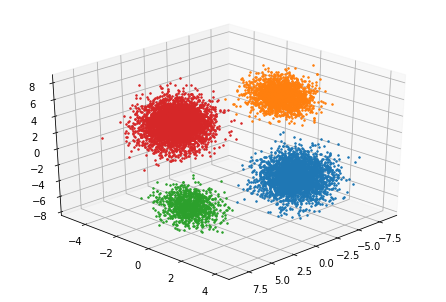
上で求めたindexをもとに，色分けして10000個のデータをプロットしています。for文で回していますが，もっと他に良い方法があれば教えていただけると助かります。
ファイル出力
with open(csv_name, 'w') as file:
writer = csv.writer(file, lineterminator='\n')
writer.writerows(gamma.T)
with open(dat_name, 'w') as file:
writer = csv.writer(file, lineterminator='\n\n')
writer.writerows(params)最後に，負担率とパラメータをファイルに出力して終了です。お疲れ様でした。
全体のコード
import numpy as np
import csv
from numpy import linalg as la
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys
txt_dir = sys.argv[1]
csv_name = sys.argv[2]
dat_name = sys.argv[3]
with open(txt_dir) as f:
reader = csv.reader(f)
l = [row for row in reader]
for i in range(len(l)):
for j in range(len(l[i])):
l[i][j] = float(l[i][j])
l = np.array(l)
def calc(x, mu, sigma_inv, sigma_det):
D = x.shape[0]
exp = -0.5*(x - mu).T@sigma_inv.T@(x - mu)
denomin = np.sqrt(sigma_det)*(np.sqrt(2*np.pi)**D)
return np.exp(exp)/denomin
def gauss(X, mu, sigma):
output = np.array([])
eps = np.spacing(1)
Eps = eps*np.eye(sigma.shape[0])
sigma_inv = la.inv(sigma)
sigma_det = la.det(sigma)
N = X.shape[0]
for i in range(N):
output = np.append(output, calc(X[i], mu, sigma_inv, sigma_det))
return output
def mix_gauss(X, Mu, Sigma, Pi):
k = len(Mu)
output = np.array([Pi[i]*gauss(X, Mu[i], Sigma[i]) for i in range(k)])
return output, np.sum(output, 0)[None,:]
def setInitial(X, k):
D = X.shape[1]
Mu = np.random.randn(k, D)
Sigma = np.array([np.eye(D) for i in range(k)])
Pi = np.array([1/k for i in range(k)])
return Mu, Sigma, Pi
def log_likelihood(X, Mu, Sigma, Pi):
K = Mu.shape[0]
D = X.shape[1]
N = X.shape[0]
_, out_sum = mix_gauss(X, Mu, Sigma, Pi)
logs = np.array([np.log(out_sum[0][n]) for n in range(N)])
return np.sum(logs)
def EM(X, k, Mu, Sigma, Pi, thr):
K = Mu.shape[0]
D = X.shape[1]
N = X.shape[0]
log_list = np.array([])
log_list = np.append(log_list, log_likelihood(X, Mu, Sigma, Pi))
count = 0
while True:
out_com, out_sum = mix_gauss(X, Mu, Sigma, Pi)
gamma = out_com / out_sum
N_k = np.sum(gamma, 1)[:,None]
Mu = (gamma @ X) / N_k
sigma_list = np.zeros((N, K, D, D))
for k in range(K):
for n in range(N):
sigma_com = gamma[k][n]*(X[n] - Mu[k])[:,None]@((X[n] - Mu[k]))[None,:]
sigma_list[n][k] = sigma_com
Sigma = np.sum(sigma_list, 0) / N_k[:,None]
Pi = N_k/N
log_list = np.append(log_list, log_likelihood(X, Mu, Sigma, Pi))
if np.abs(log_list[count] - log_list[count+1]) < thr:
return count+1, log_list, Mu, Sigma, Pi, gamma
else:
print("Previous log-likelihood gap:" + str(np.abs(log_list[count] - log_list[count+1])))
count += 1
thr = 0.01
k = 4
Mu, Sigma, Pi = setInitial(l, k)
n_iter, log_list, Mu, Sigma, Pi, gamma = EM(l, k, Mu, Sigma, Pi, thr)
print("Iteration:"+str(n_iter))
print("log-likelihood:"+str(log_list))
params = np.array([Mu.ravel(), Sigma.ravel(), Pi.ravel()])
index = np.argmax(gamma, 0)
cm = plt.get_cmap("tab10")
fig = plt.figure()
ax = Axes3D(fig)
N = l.shape[0]
for n in range(N):
ax.plot([l[n][0]], [l[n][1]], [l[n][2]], "o", color=cm(index[n]), ms=1.5)
ax.view_init(elev=30, azim=45)
plt.show()
with open(csv_name, 'w') as file:
writer = csv.writer(file, lineterminator='\n')
writer.writerows(gamma.T)
with open(dat_name, 'w') as file:
writer = csv.writer(file, lineterminator='\n\n')
writer.writerows(params)
●PRML「パターン認識と機械学習＜第９章＞」
「下界とKLダイバージェンスはどちらから注目していけばいいのでしょうか。それは，qのみに依存しているKLダイバージェンスです。」と記載されているのですが、KLダイバージェンスは分子部分がp(Z|X,θ)であり、θにも依存しているように思うのですが。なぜ、qのみに依存しているのでしょうか。逆に言うとなぜL(q,θ)はqとθに依存するのでしょうか？
go様
ご返信が遅れまして，大変失礼致しました。（通常であれば1日以内の返信を心掛けています）
ご指摘誠にありがとございます。少し考えてみたのですが，確かにKLダイバージェンスと下界はどちらも「$\theta$」「$q$」に依存していますよね（というより，依存していなければEMのような反復操作に基づく近似は不可能）。ですので，EMではどちらのステップから初めてもOKだと思います。
本文を少し修正いたしました。勉強になりました！
このプログラムを実装したいのですが、元の.csvファイルの10000個の３次元データはどのように保存されているのでしょうか？
sa様
ご連絡ありがとうございます。
また，ご返信が遅くなり大変申し訳ありません。
csvファイルのデータは適当に作成したものでして，現在手元にはありません>< 3次元空間を4つに分割して，それぞれで乱数を発生させることで似たようなデータを作成することが可能です。 お手数ですが，お試しいただけますと幸いです。