【超初心者向け】ガウス過程とは？出来る限り分かりやすく簡潔に説明します。

この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多少意訳した部分もあります。ですので，参考程度におさめていただければ幸いです。

間違えている箇所がございましたらご指摘いただけますと助かります。随時更新予定です。他のサーベイまとめ記事はコチラのページをご覧ください。

ガウス過程とは？

 

ガウス過程というのは，面に関数が書かれたサイコロのことです。つまり，ガウス過程からは関数が出力されるのです。

ガウス過程を使うことで，何が嬉しいのでしょうか。

このように，ガウス過程はベイズに基づく手法なので，データが十分に存在する場所では自信のある出力（分散が小さい）をして，データが足りない場所では自信の無い出力（分散が大きい）をします。また，昔からガウス過程は単一層のニューラルネットワークとの等価性が示されていましたが，最近になって深層学習との完全な対応関係も示されました。詳しくは，以下の記事をご覧ください。

【サーベイまとめ】ガウス過程と深層学習の美しい関係。出来る限り分かりやすく簡潔に説明します。この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多...

 

以下では，ガウス過程を３つの側面からお伝えしていこうと思います。

 

ガウス過程の説明①

ガウス過程は，無限次元のガウス分布です。

 

 

「無限次元のガウス分布」とは，入力と出力がそれぞれ無限次元のガウス分布のことを指します。そして，各入力と各出力は，それぞれガウス分布に従っています。

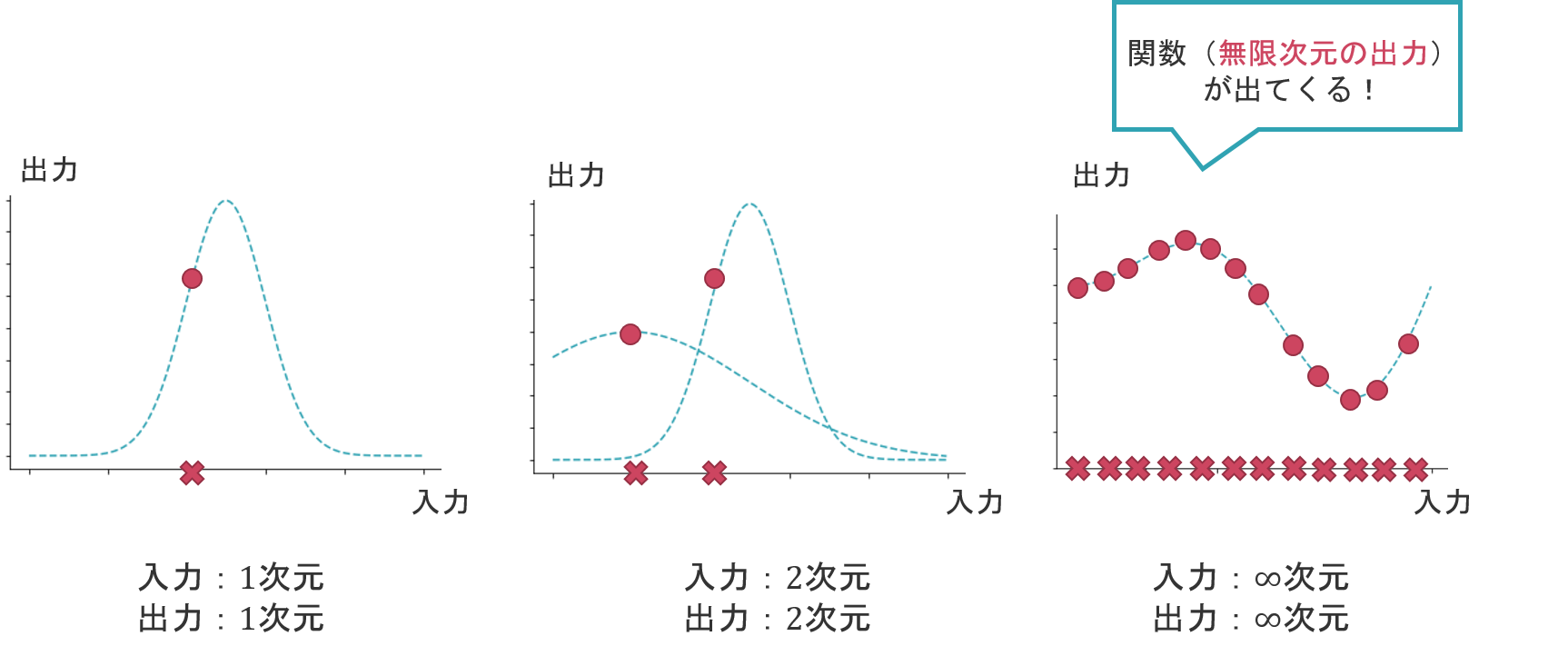
無限次元の出力というのは，いわば関数そのものです。つまり，全てガウス分布に従う無限次元の入力から，無限次元の出力が得られるというこの機構こそ，ガウス過程のことを指しているのです。

 

ガウス過程の説明②

ガウス過程は，線形回帰モデルの無限次元への拡張です。線形回帰モデルを無限次元に拡張する前に，簡単に線形回帰モデルを復習しておきましょう。

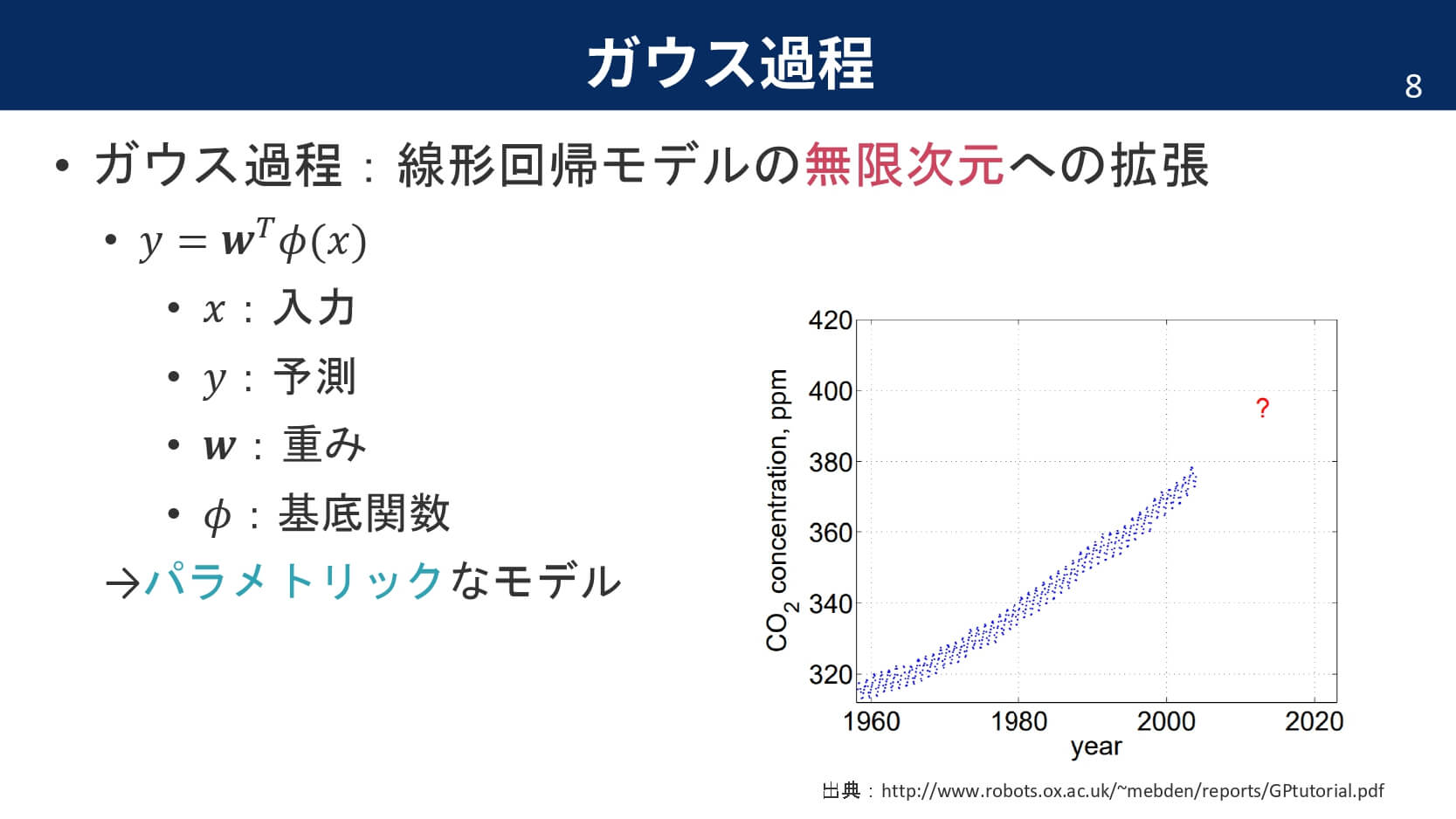
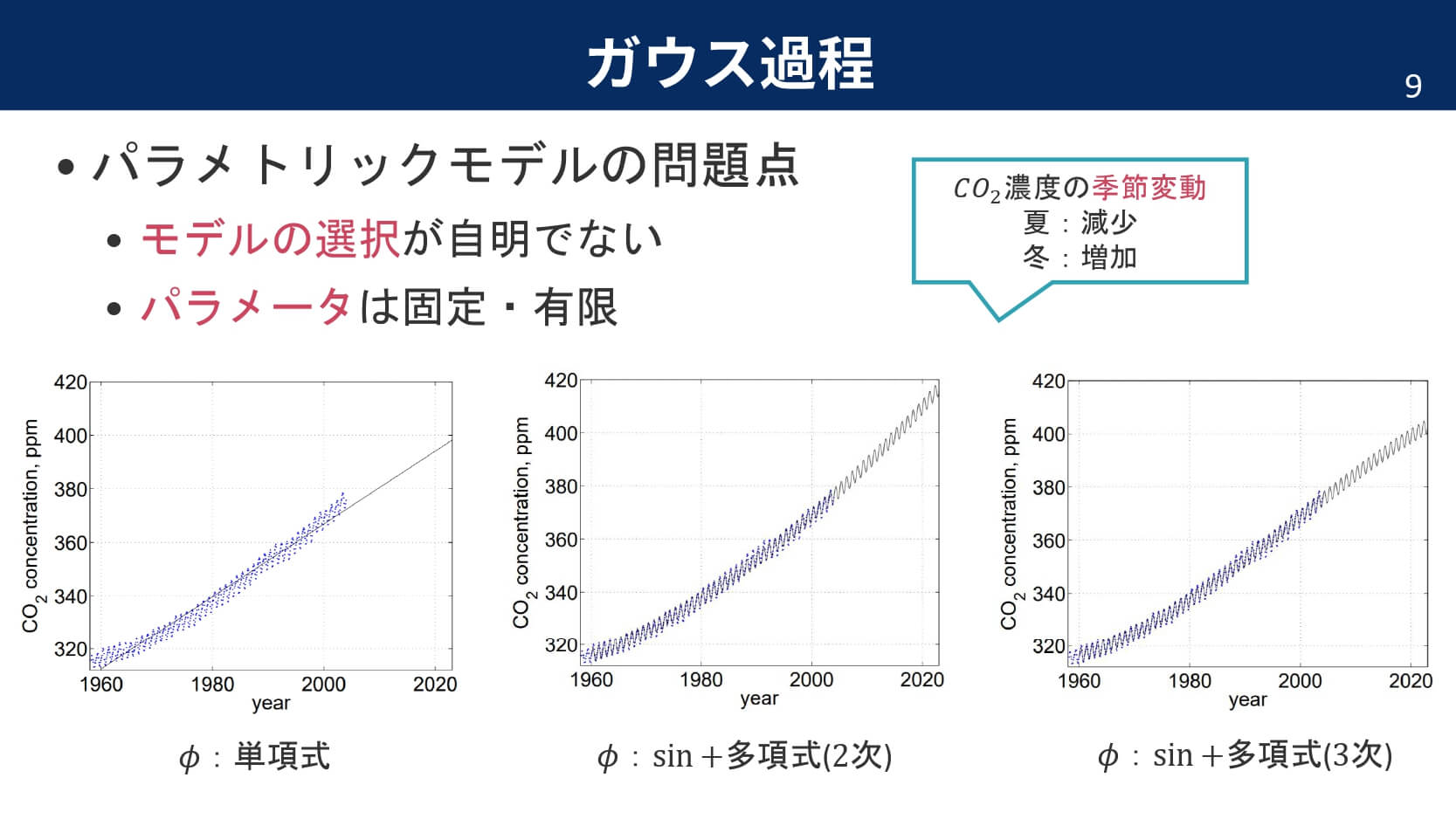
つまり，パラメータを分布という確率密度で表現してあげることで，あいまいさを持たせた状態でモデル化できるという訳です。さて，ここからは線形回帰モデルを行列で表して，事前分布の仮定を導入していきます。

ガウス分布というのは，ガウス分布に従う入力が与えられたときに，出力もガウス分布に従うようなモデルのことを指します。それでは，事前分布を導入して線形回帰モデルがガウス過程の定義にマッチすることを確認しましょう。

見事，出力$\boldsymbol{y}$もガウス分布に従うことが示されました。ここで，最初のサイコロの例に戻ってみましょう。出力である関数が$\mathcal{N}(\boldsymbol{0},\boldsymbol{K})$に従うというのは，$N$次元の中で定義される多次元正規分布の中の１点が，ある１つの関数に対応しているということを意味しています。つまり，サイコロを振るという操作は，多次元正規分布から１点をサンプリングするという操作と同じなのです。

 

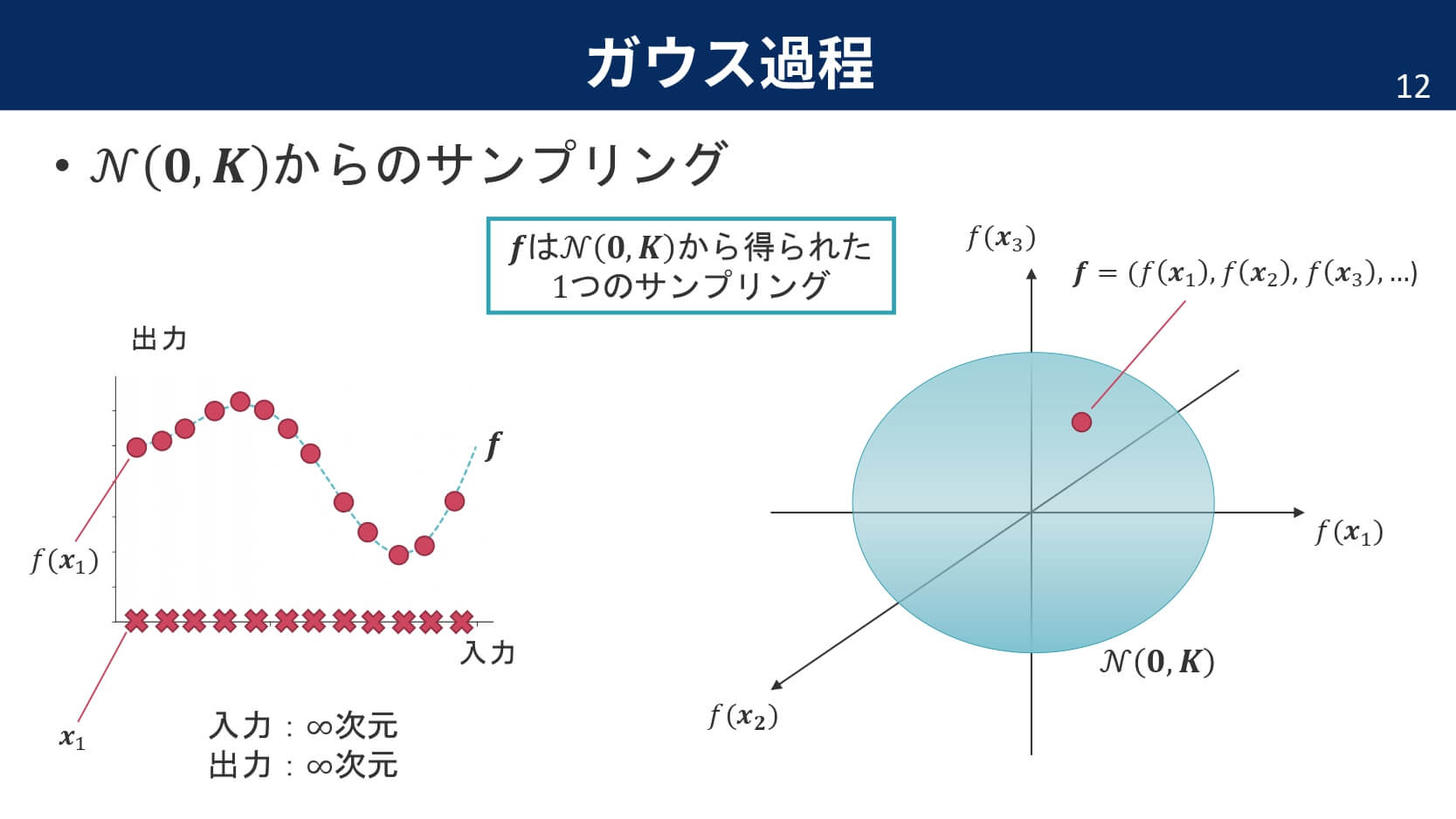
さて，ここでカーネルに関しても復習しておきましょう。カーネルというのは特徴ベクトルの内積で定義され，距離尺度のような意味合いを持ちます。

カーネルを説明するためによく利用される例が，カーネルトリックです。下の図は，分類タスクで二次元では線形分類することが難しそうな例でも，カーネルによって高次元へと変換することで，超平面により分離が可能になっている例を表しています。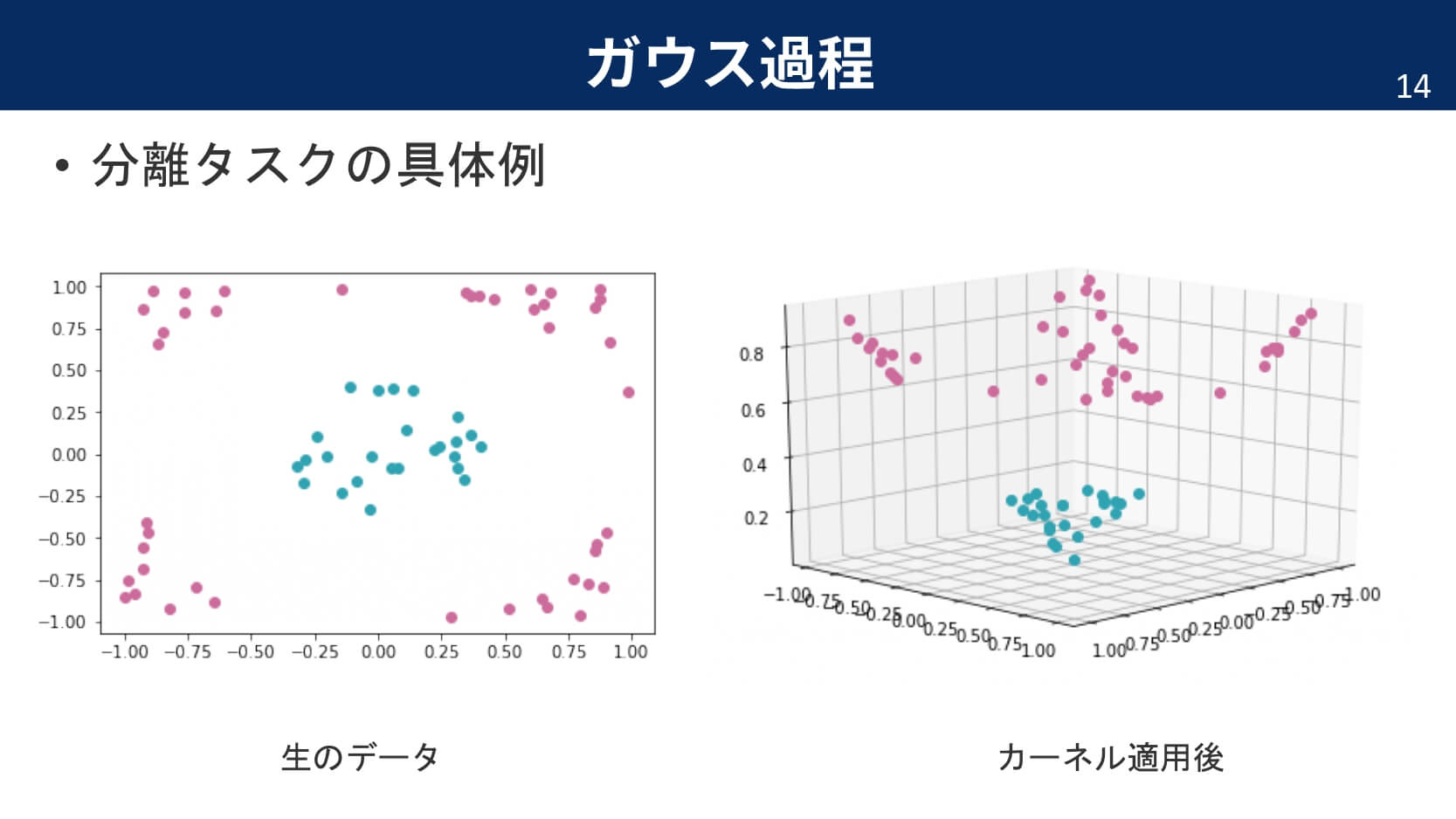

このカーネルが，ガウス過程では非常に重要な役割を果たします。線形回帰モデルを無限次元へと拡張するにあたり，今回は自然な流れとして，カーネルにガウスカーネルを仮定してみることにしましょう。実は，ガウスカーネルを仮定していること自体が，線形回帰モデルの無限次元への拡張を表しています。というのも，ガウスカーネルというのは$M\rightarrow\infty$とした無限次元特徴ベクトルの内積で表されるからです。

ここまでをまとめてみます。線形回帰モデルでパラメータの事前分布にガウス分布を仮定すると，出力もガウス分布になります。つまり，ガウス過程です。カーネルとしては何を仮定してもよいのですが，特にガウスカーネルを仮定すると，$\phi$にガウス基底を仮定していることになります。また，簡単な変形により，ガウスカーネルが無限次元の特徴ベクトルの内積で表されることが分かりました。

 

ガウス過程の説明③

ガウスカーネルは，基底関数に「平均を無限個用意したガウス分布を仮定する」という説明もできます。だからこそ，ガウスカーネルを利用したガウス過程の出力は滑らかな関数になるのです。

 

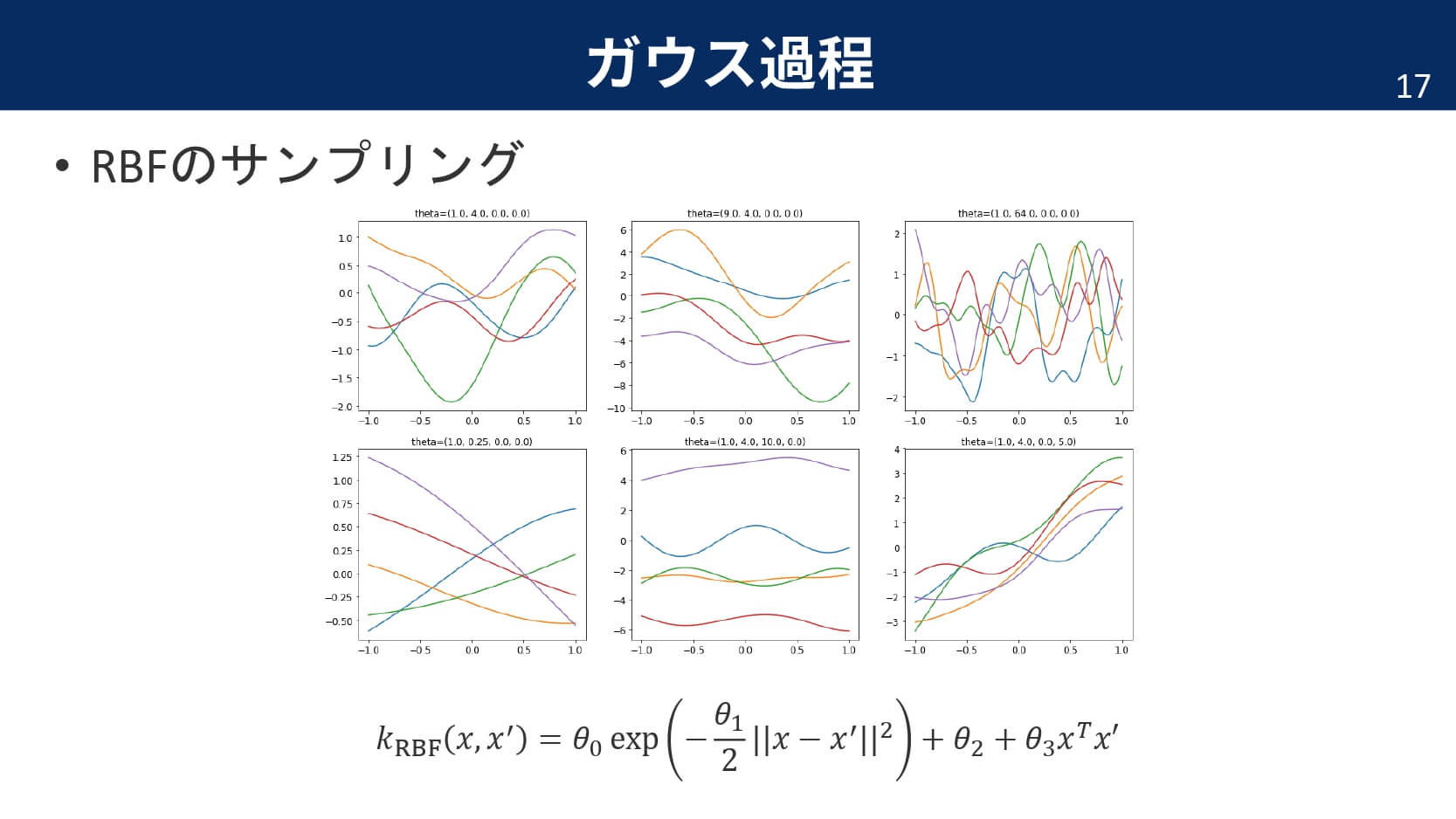
実際はノイズが付加される

今までは，モデルの出力が単純に特徴ベクトルの線形和だったのですが，実際にはノイズとして$\epsilon$が加えられます。ノイズがガウス分布に従って発生したとすれば，ガウス分布の畳み込みの性質から出力もガウス分布に従うことが分かります。

 

ガウス過程の予測分布

さて，ここからがガウス過程のミソです。線形回帰モデルの予測は，単に最適化されたパラメータ$\boldsymbol{w}$を使って重みづけ和を計算すればOKでした。しかし，今回の場合は重みパラメータを全てカーネルというくくりの中で表してしまっているため，重みパラメータを明示的に求めている訳ではないのです。そこで，ガウス過程の予測分布では「行列でひとまとめに表してしまう」というアイディアを利用します。

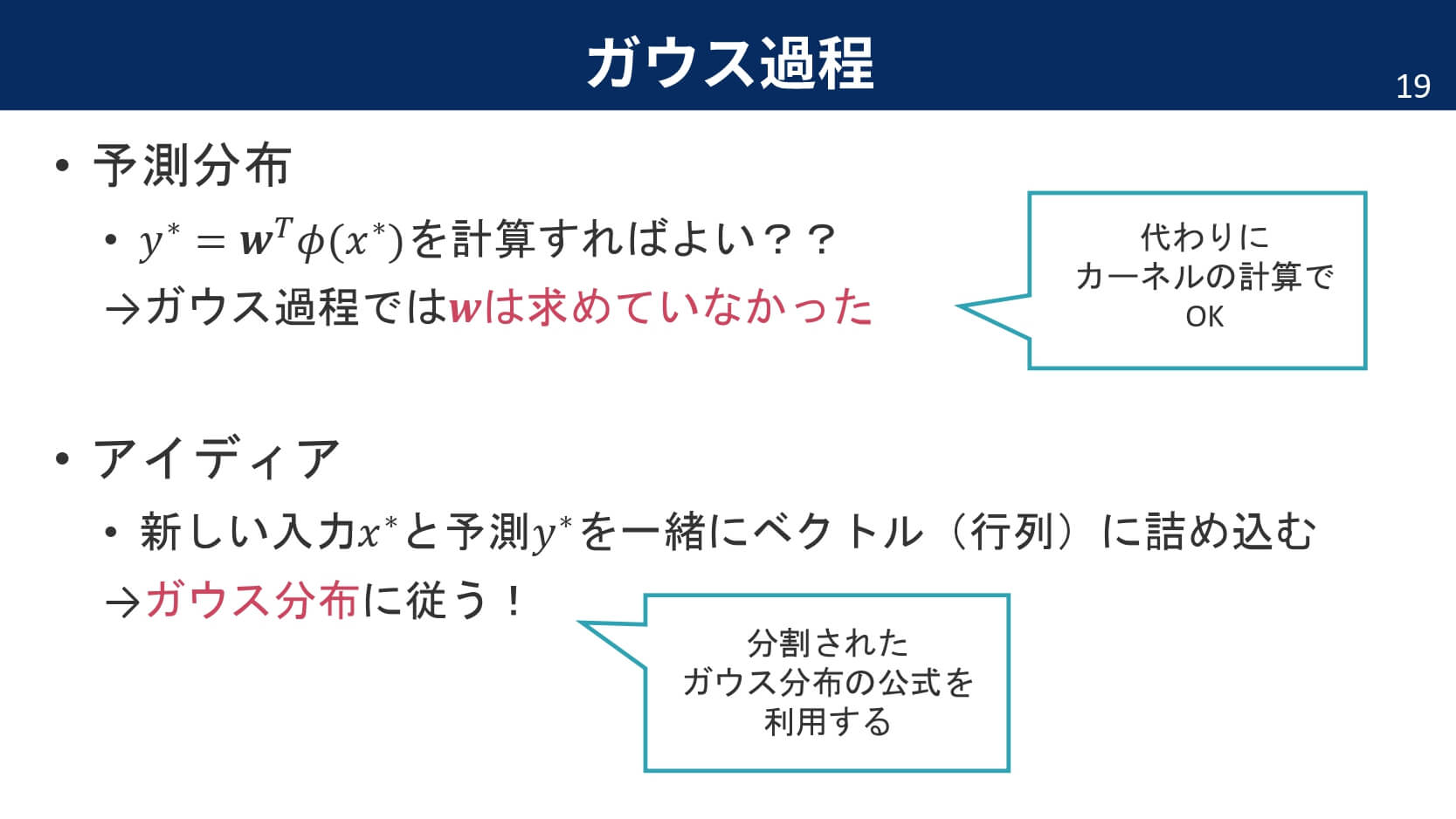
参考の式は，PRMLでも証明されている通りです。

 

イメージアニメーション

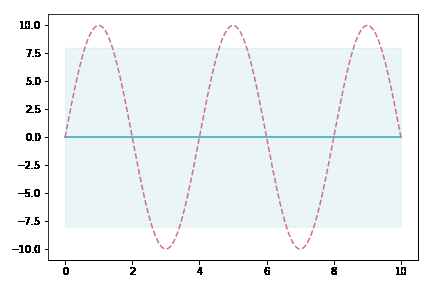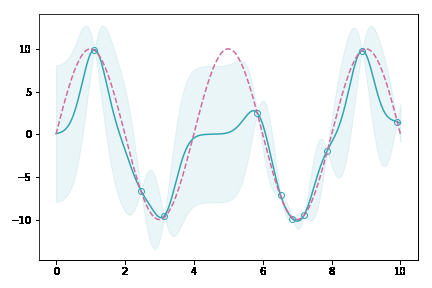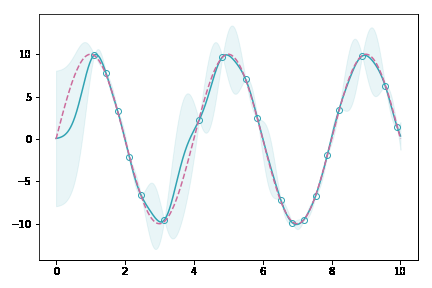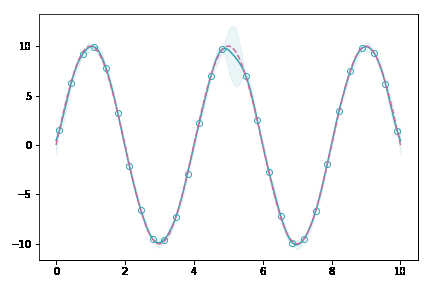
データ点が増えていくにしたがって，薄緑（分散を表している）の領域がどんどん狭まっていくのが分かると思います。これは，ガウス過程がベイズに基づく手法であることを裏付けています。データがある場所では自信満々に，無い場所ではあいまいさを持たせて出力するモデルなのです。

 

大問題

メリットばかりだと思われるガウス分布ですが，実は大問題があります。それは，カーネル行列の計算です。

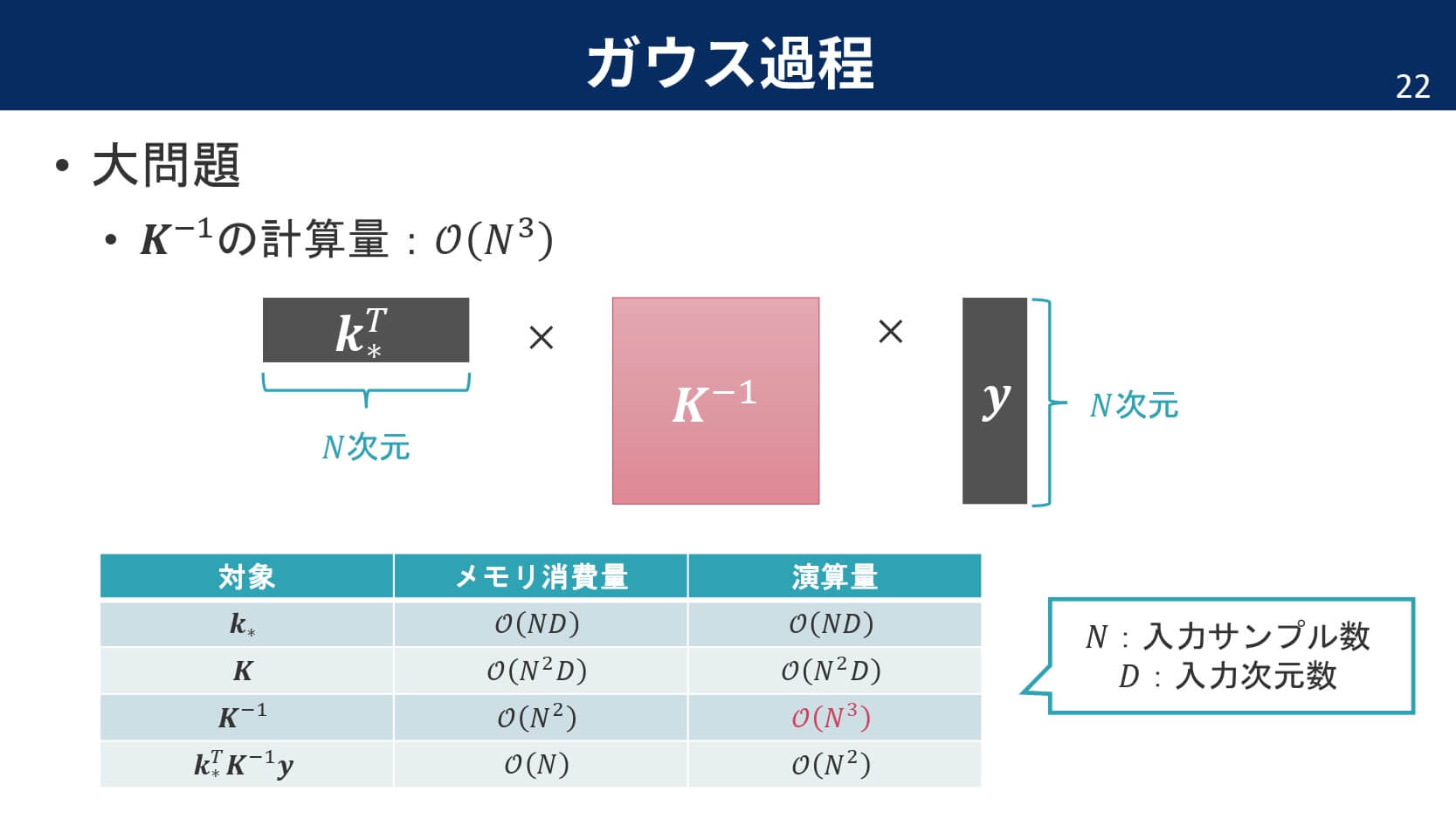
サンプル数の$3$乗だけ計算量がかかってしまうのです。この大問題を克服するために，先人たちは多くの手法を考案してきました。

 

まとめ

ガウス過程は，関数が面に書かれたサイコロのようなものでした。ガウス分布に従う事前分布を導入することで，線形回帰モデルはガウス過程となりました。ガウス分布に従うノイズを導入した場合も，出力はガウス分布に従いました。ガウス過程の予測分布は，行列計算を分割して，公式をうまく利用することで求めることが可能です。

ガウス過程の予測分布は，カーネルのみで表すことができている点が重要です。ここでも，重みパラメータを明示的に扱っている訳ではありません。カーネルの世界で話を進めているのです。また，ガウス過程の大問題はカーネル行列の計算ですが，計算量を減らすために多くの取り組みがなされてきました。

 

おすすめ参考書

超おすすめの参考書になります。本記事も，コチラの書籍を参考にさせていただいた部分が大きいです。ガウス過程だけでなく，「機械学習とはなにか」という本質部分も柔らかな口調で解説されており，「第０章だけでも読んでいってください!!」という帯宣伝通り，ガウス過程を知りたいという読者以外の方にもおススメできる参考書になっています。