この記事では,研究のサーベイをまとめていきたいと思います。ただし,全ての論文が網羅されている訳ではありません。また,分かりやすいように多少意訳した部分もあります。ですので,参考程度におさめていただければ幸いです。
間違えている箇所がございましたらご指摘ください。随時更新予定です。他のサーベイまとめ記事はコチラのページをご覧ください。
読みたい場所へジャンプ!
ガウス過程とは?

詳しくは,上の記事をご覧ください。
ガウス過程と深層学習
実は,1990年代からニューラルネットワークと深層学習の関係性は指摘されていました。具体的には,隠れ層が1層のニューラルネットワークで隠れ層のユニット数を$\infty$にすると,ニューラルネットワークの出力はガウス過程と等価になるというのです。特に重要なポイントは,独立な確率密度関数の和が正規分布に従うようになる中心極限定理です。
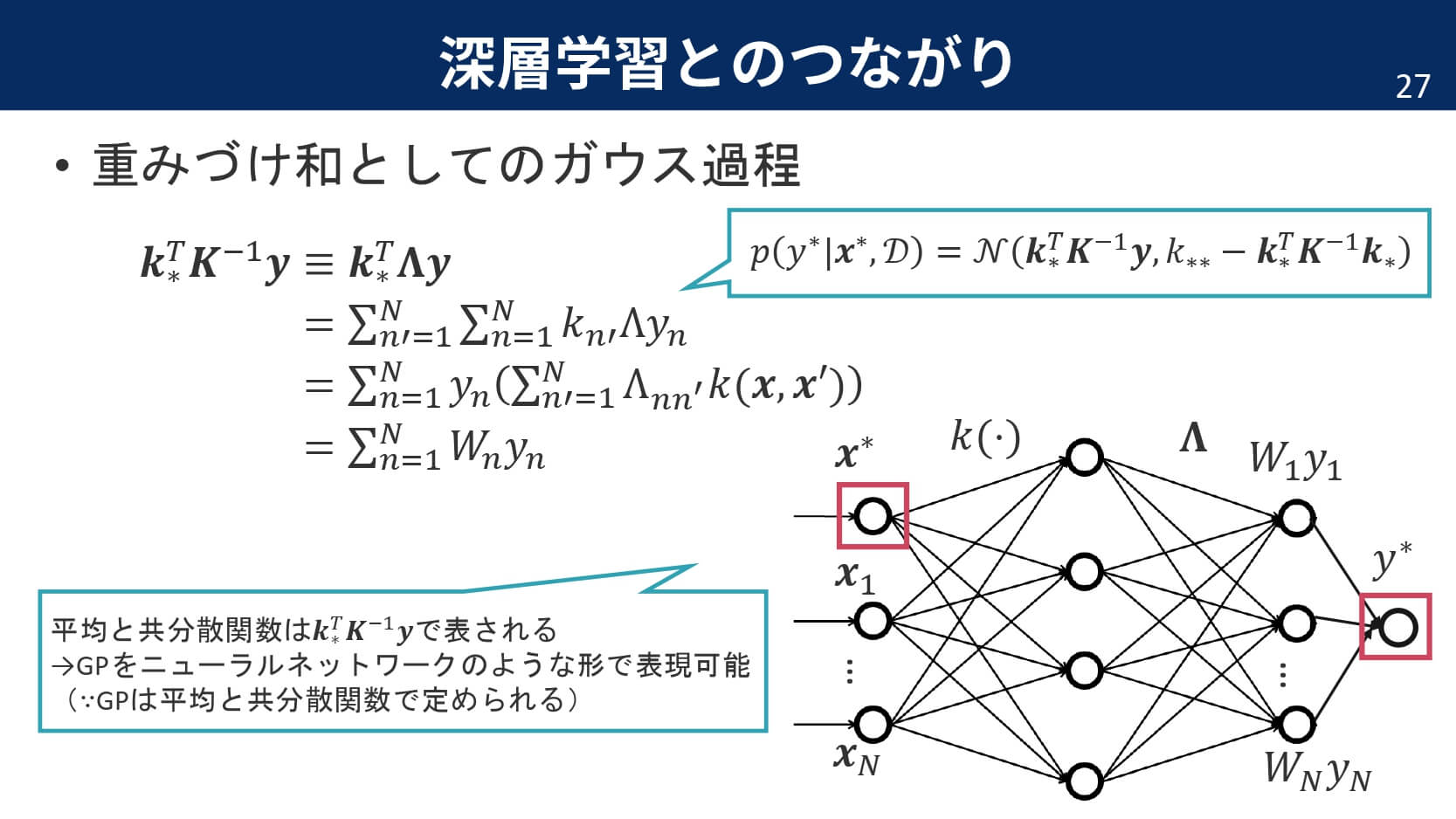

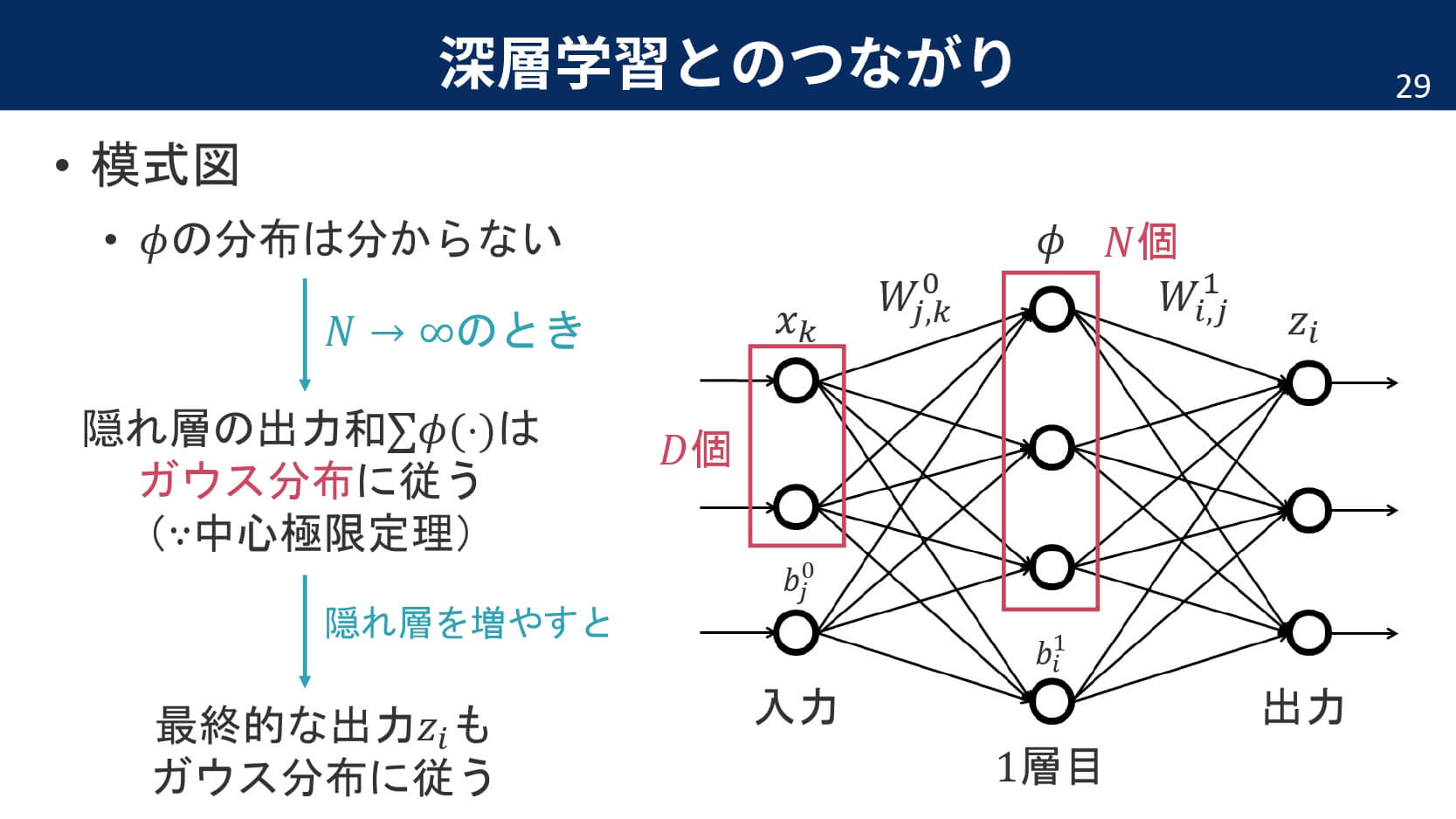
今回は,カーネル関数として出力の積の期待値を定義します。こうすることで,隠れ層が1層だけのニューラルネットワークから$L$層のニューラルネットワークへと再帰的な拡張が可能になります。
というのも,カーネルを計算するとまたまた「積の期待値」という形が出現するのです。これにより,隠れ層が1層の場合のカーネルの計算結果を参考にして,$l$層目のカーネルを再帰的に定義することができます。ここでは,期待値は積分計算を含みますので,結果を$\phi$に依存する適当な関数$F_{\phi}$として表してしまいます。この際,層を重ねていることから,項として自分自身とのカーネルも含むことに注意が必要です。

勝手に定義した$F_{\phi}$ですが,非線形関数がランプ関数ReLUのときには解析的に求められることが分かっています。
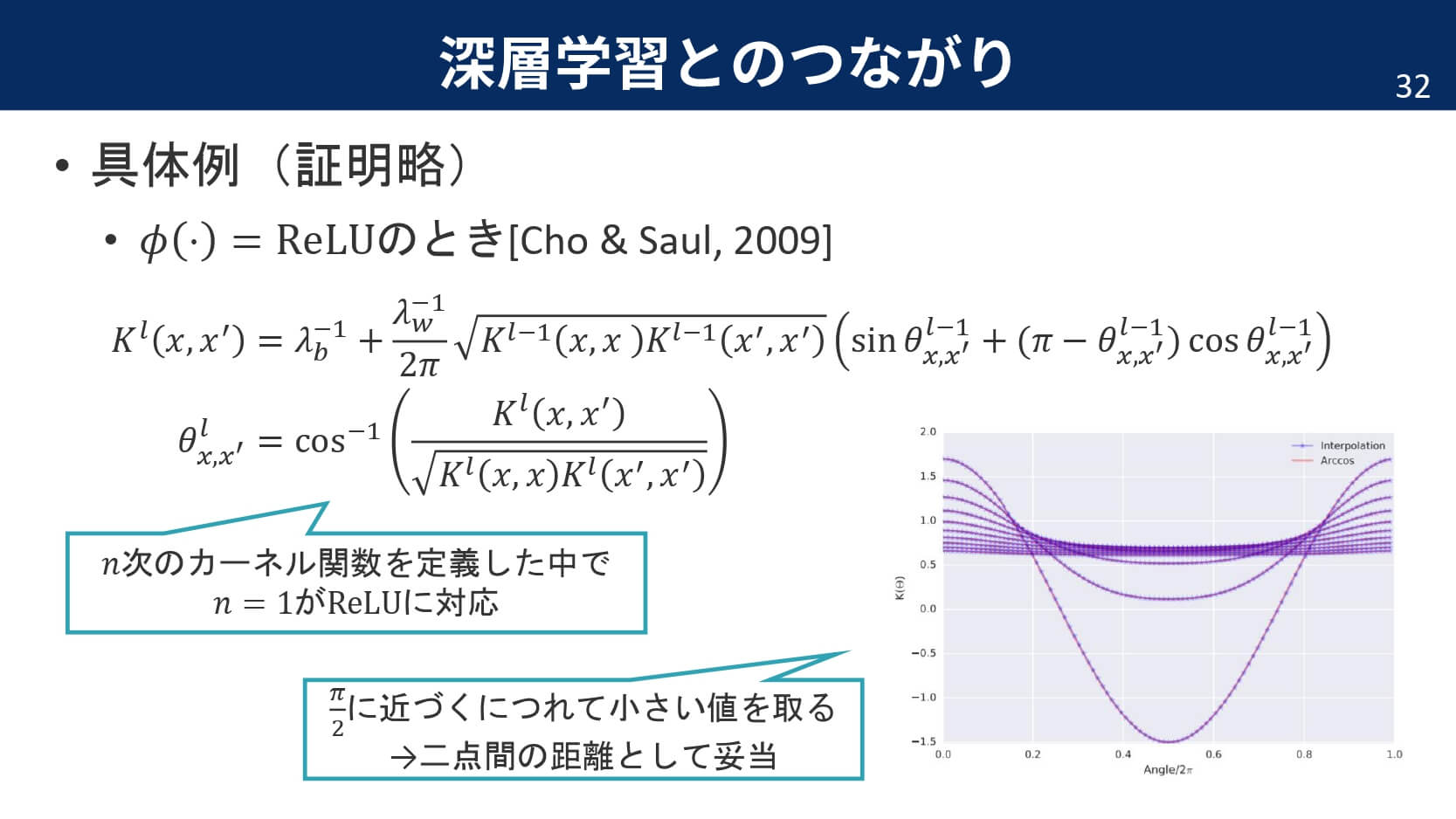
しかし,非線形関数$\phi$に依存する$F_{\phi}$は他の非線形関数であった場合にはどう計算すればよいのでしょうか。そこで,Leeらは以下のようなルックアップテーブルを作成して,線形補間に基づくアイディアで近似しようと試みました。特筆すべきなのは,従来のDNNでは複雑な最適化アルゴリズムを経て出力を得ることができたわけですが,今回の「ガウス過程としての深層学習モデル」では,単なる行列計算によりパラメータの更新が可能になている点です。

こちらの式は,どうやらガウス積分近似に対応しているようです。力不足で,詳細については読み取ることができませんでした。
実験結果
以下,論文中の主な実験結果と,そこから分かったことをまとめています。
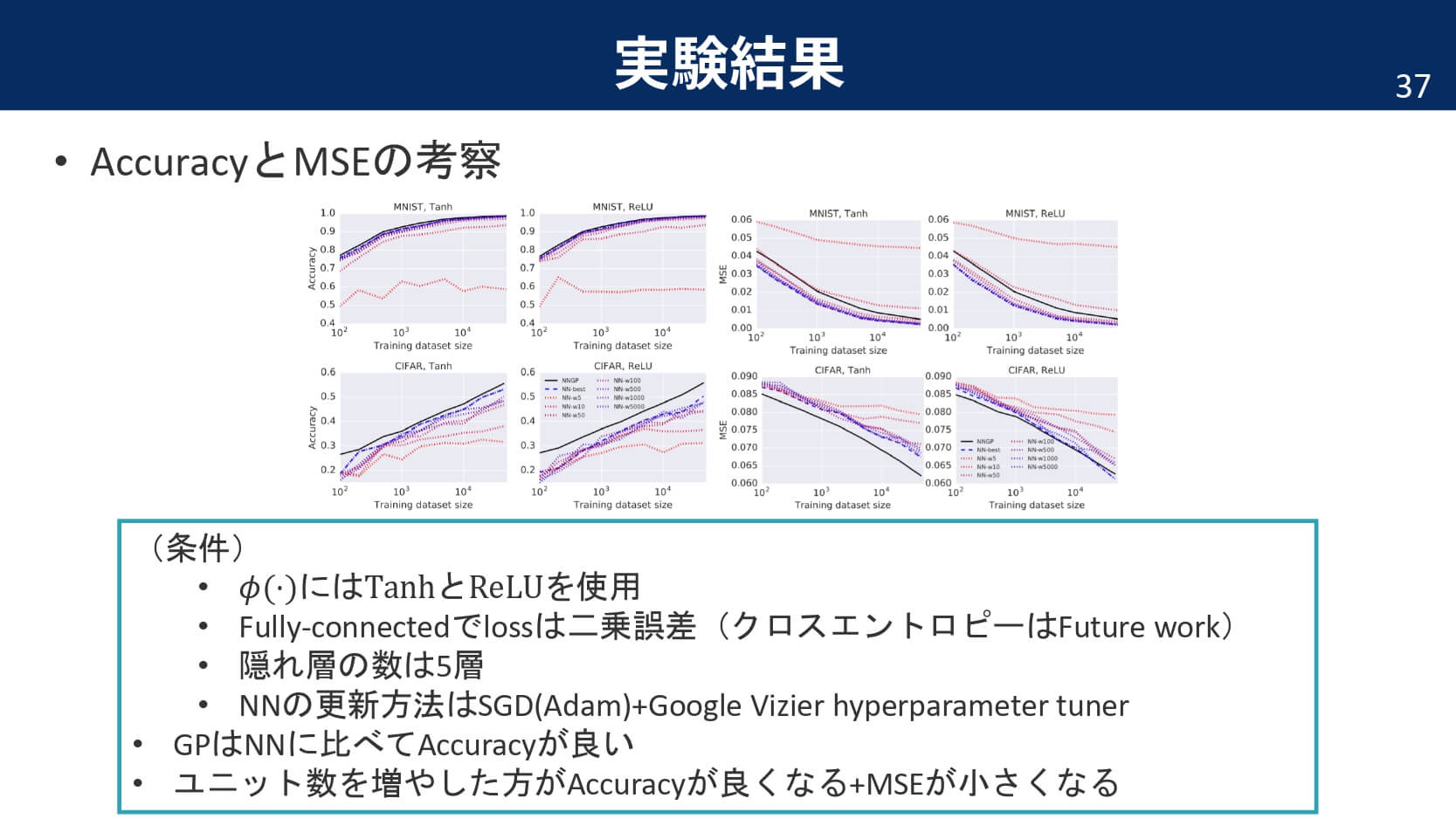

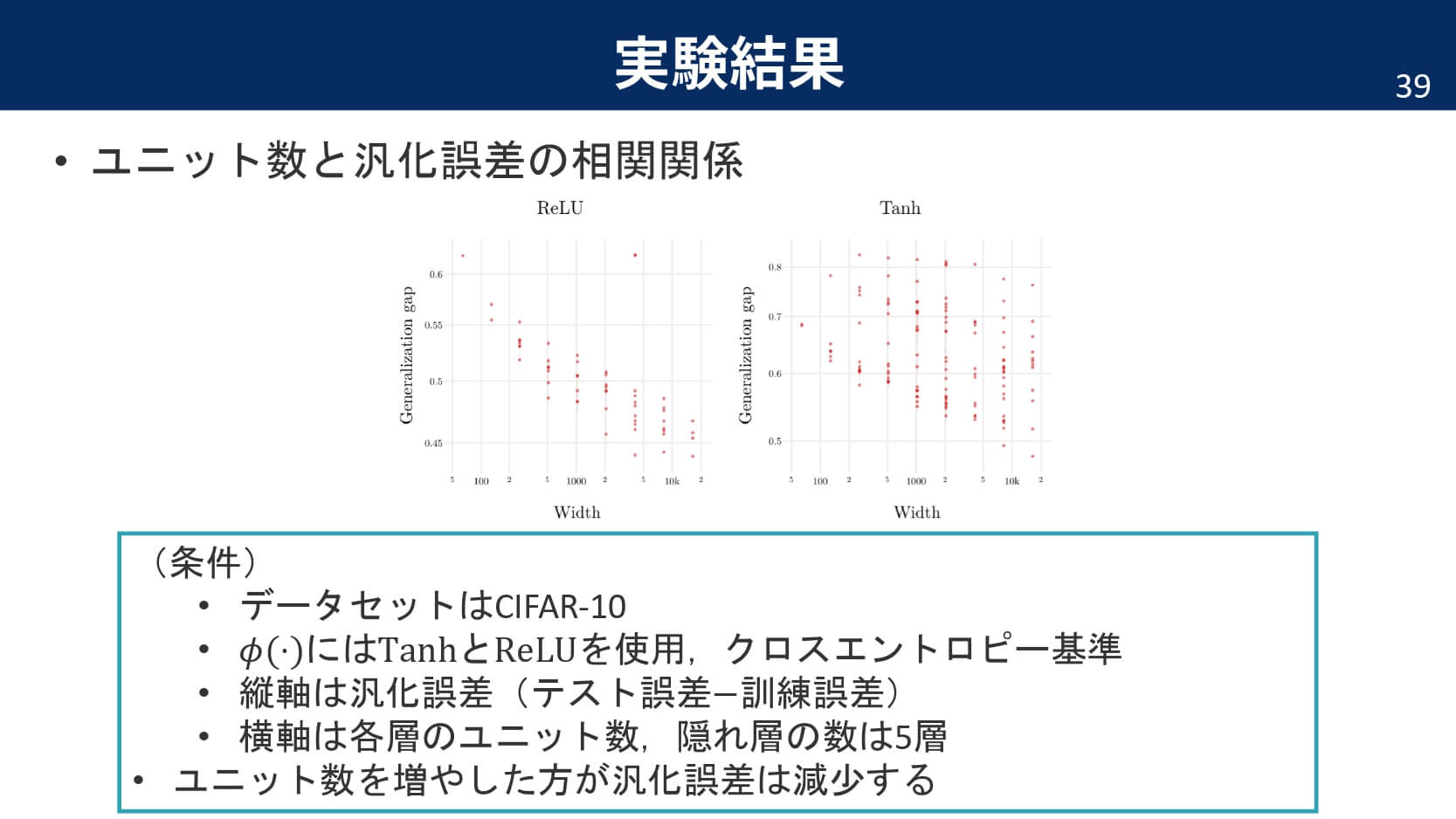
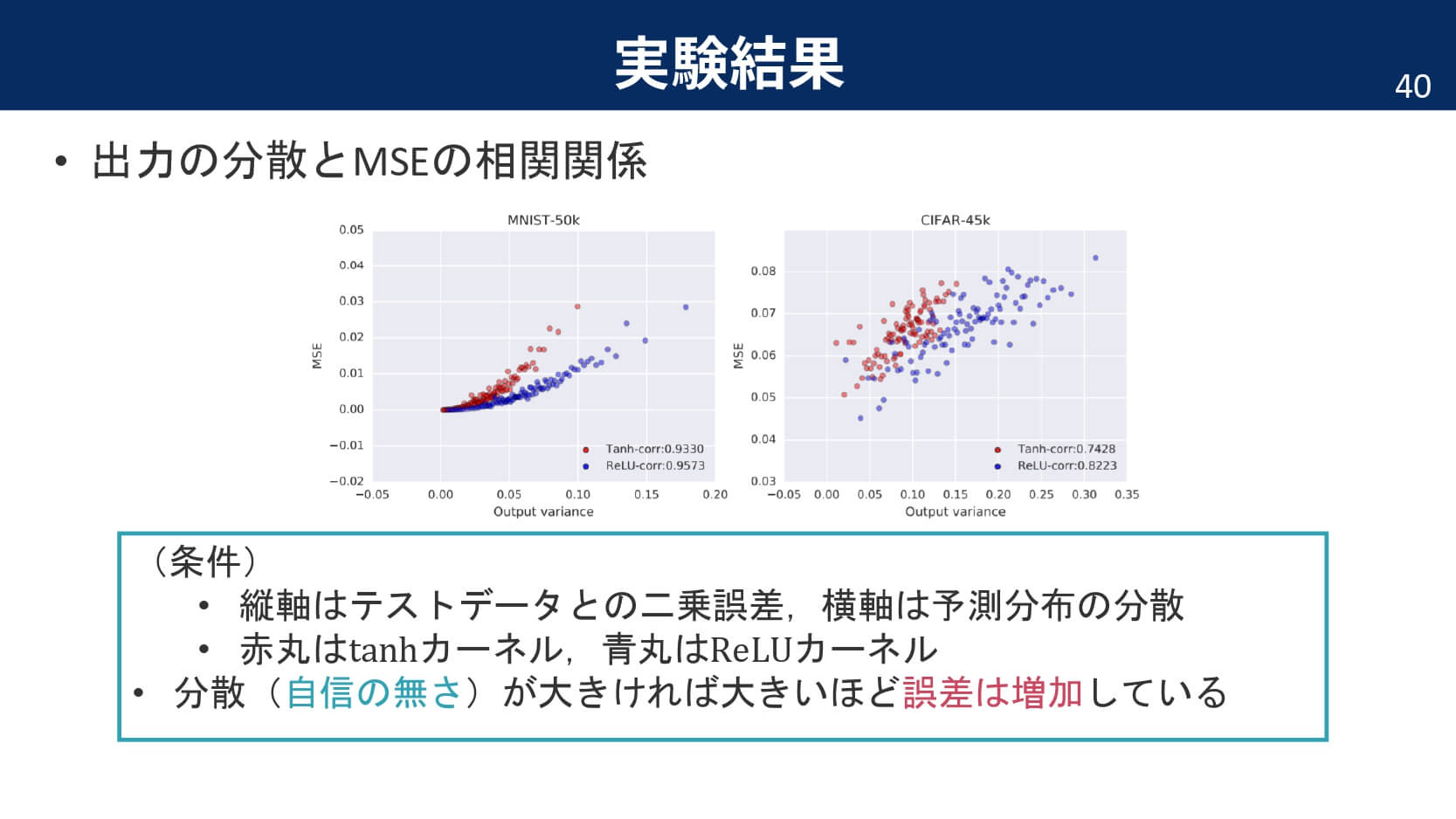
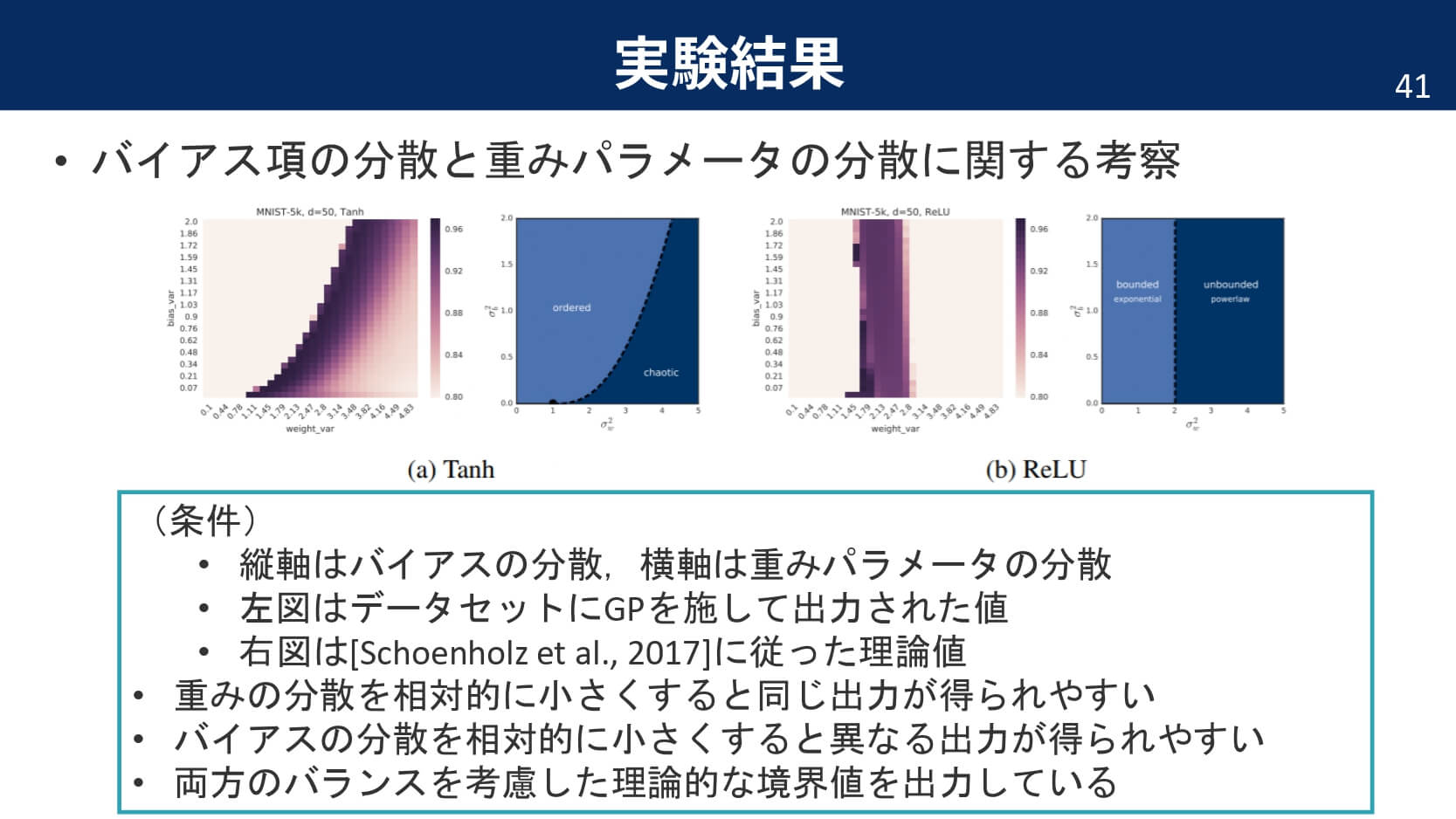
まとめ
最後に,まとめです。

おすすめ参考書
超おすすめの参考書になります。本記事も,コチラの書籍を参考にさせていただいた部分が大きいです。ガウス過程だけでなく,「機械学習とはなにか」という本質部分も柔らかな口調で解説されており,「第0章だけでも読んでいってください!!」という帯宣伝通り,ガウス過程を知りたいという読者以外の方にもおススメできる参考書になっています。
●Pattern Recognition and Machine Learning, Christopher Bishop


















