この記事では,マルチメディア通信に関わる知識を簡単にまとめていきたいと思います。ただし,全ての知識が詳しく網羅されている訳ではありません。また,分かりやすいように多少意訳した部分もあります。ですので,参考程度におさめていただければ幸いです。
間違えている箇所がございましたらご指摘ください。随時更新予定です。他のマルチメディア通信に関する記事はコチラのページをご覧ください。
暗号の概要
こちらのスライド[外部リンク:現代暗号〜ネット社会の情報を守る暗号技術とは〜]でも解説されているように,暗号は以下のように発展してきました。
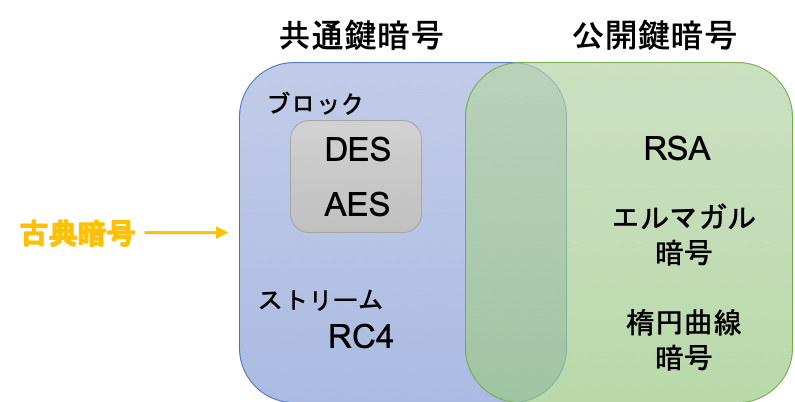
●古典暗号
・シーザー暗号
・単一換字暗号
・機械式暗号(エニグマ)
(弱点は頻度分析)
●現代暗号
★2つの安全性
・計算量
・情報量
★2つの方式
<共通鍵暗号>
ーブロック暗号
ーDES
ーAES
ーストリーム暗号
ーRC4
<公開鍵暗号>
ーRSA
ーエルガマル
ー楕円曲線
それぞれの概要は,以下の記事に簡単にまとめてあります。ここでは,エニグマ/DES/トリプルDES/AESについて補足しておきます。
エニグマ
エニグマまでの発展に関しては,こちらのYoutubeチャンネルの解説が分かりやすいです。ここでは,簡単に要約していきます。
まず,古典暗号は「単一換字暗号→多表式換字暗号→ワンタイムパッド」というように発展していきました。単一換字暗号は,ある文字を特定の規則(鍵)に従って置き換える方法です。アルファベットを特定の数だけずらすシーザー暗号や,乱数との排他的論理和を取るヴァーナム暗号が挙げられます。しかし,単一換字式暗号は,総当たり攻撃を仕掛ければ簡単に破られてしまいます。
そこで,文字の置き換え方を複数の規則(鍵)に従って置き換えるようにした方法が,多表式換字暗号です。アルファベット方陣を作って,縦軸を平文のアルファベット,横軸を鍵のアルファベットとして,毎回置き換え方を変えるヴィジュネル暗号などが該当します。しかし,こちらも置き換えのパターンの頻度分析を行うことによって破られてしまいます。
そこで考案されたのが,複数の規則を一定時間ごとに変えてしまおうというワンタイムパッドの考え方です。暗号化のための鍵について,wikipediaより引用します。
暗号化・復号の鍵は、いくつかあるローターのうちどの3枚を使うかの組み合わせと、ローターをセットする順序、ローターの目盛りの初期位置、およびプラグボード配線である。
Wikipedia [エニグマ (暗号機)]
これらの組み合わせにより,毎回文字の置き換え規則を変えた暗号がエニグマです。しかし,エニグマも戦時中にポーランドやイギリスの暗号解読軍によって行われた頻度分析によって解読されてしまいます。
DES
DES(Data Encryption Standard)は共通鍵暗号として広く利用されてきた暗号化方式です。当時の標準データ暗号化規格でもありました。しかし,56bitの鍵で64bitの平文を暗号化するブロック暗号であったため,総当たり攻撃などで解読されてしまうという弱点がありました。
そこで,DESを二回行う「ダブルDES」が考案されましたが,暗号化の方向と復号の方向の両側から解読を試みる中間一致攻撃によって破られてしまいます。ダブルDESを発展させた「トリプルDES」は,「暗号化→復号→暗号」という順番でDESを3回繰り返して利用する方法で,3回とも異なる鍵を利用します。ちなみに,3回とも同じ鍵を利用すれば,実質的にDESを単独で利用した場合と等価になります。
DESについては,こちらの連載[外部リンク:マスターID/暗号技術]が非常に分かりやすいです。ここでは,簡単に要約したものをまとめます。
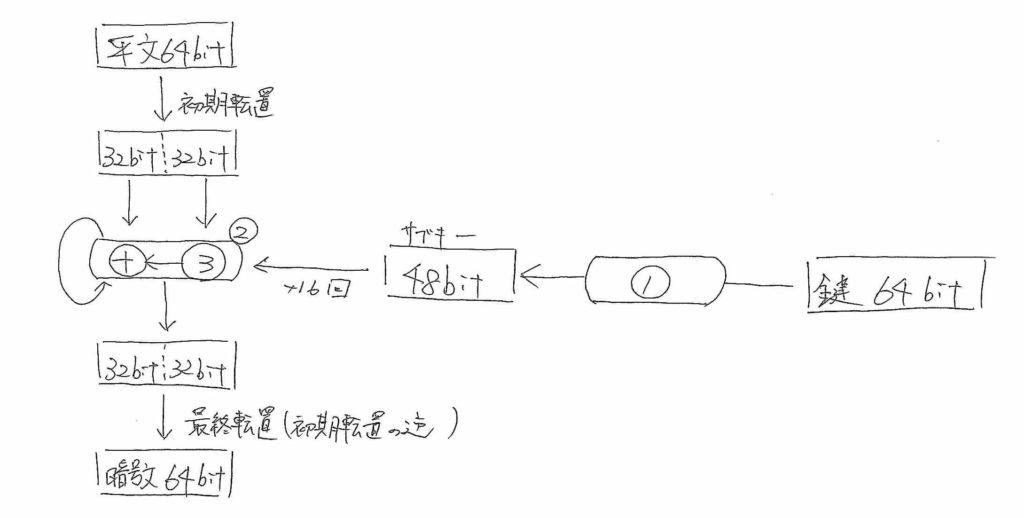
まず,DESは平文としては64bitのみ入力として受け付けます。次に,入力を転置した後に,64bitを上位32bitと下位32bitに分割します。一方で,鍵64bitからサブキー48bitを生成します(①)。サブキーと入力の下位32bitに処理を施し(③),その出力32bitと入力の上位32bitの排他的論理和を取ります(②)。これらの操作①〜③を16回繰り返し,最終的に初期転置の逆操作を行なったものを暗号文として出力します。
①の操作に関しては,パリティビット8bitを除いた56bitのうち,上位32bitと下位32bitの縮約転置(ビットデータの抽出)とシフトを行いながら②の各フェーズにおけるサブキー48bitを生成します。
②の操作に関しては,下位32bitを48bitに拡大転置したものと,①で生成した48bitのサブキーの排他的論理和を取ります。その48bitのうち,各6bitごとにルックアップテーブル(③)から4bitを参照して合計32bitを出力します。
③のルックアップテーブルは両端の2bitで行,真ん中の4bitで列を指定することで4bitを生成するような表をあらかじめ作成しておきます。
AES
AES(Advanced Encryption Standard)は,DESの安全性を指摘された後に作られた暗号化方式です。鍵長は128/192/256bit,ブロック長は128bitとなる可変長のブロック暗号です。鍵長が128bitであるAES-128でも,それなりの安全性を有しています。
DESでは,入力を半分に分割してそれぞれに対して処理を行なっていました。しかし,それでは十分な攪拌効果が得られないとして,AESでは各ビットごとに処理を行えるように「置換/シフト/混合/XOR演算」を1セットとして10回程度繰り返します。こうすることで,入力の全データに対してまんべんなく処理を行うことができます。
共通鍵暗号
共通鍵暗号では鍵交換が問題となりますが,Diffie Helmanの鍵交換方式を利用することで,うまく共通鍵を共有することができます。Diffie Helmanの鍵交換に関しては,以下の記事をご覧ください。

公開鍵暗号
公開鍵暗号としては,RSA・エルガマル暗号・楕円曲線暗号が代表的です。RSAに関しては,以下の記事をご覧ください。ここでは,エルガマル暗号と楕円曲線暗号に関して補足していきます。

エルガマル暗号
エルガマル暗号はRSAとは違って,乱数を用いるアルゴリズムのため確率的な振る舞いをします。しかし,ベースとなる考え方はDiffie Helmanの鍵交換方式と同じです。
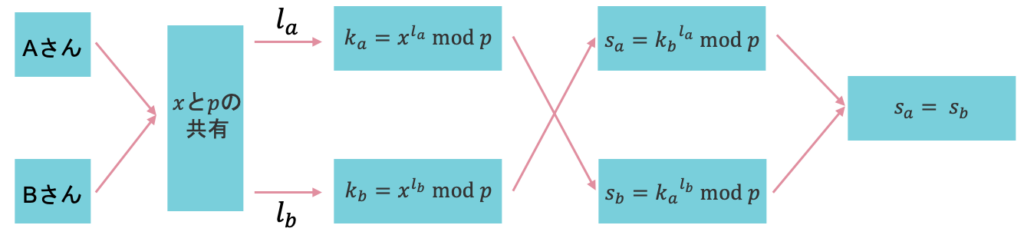
Diffie Helmanの鍵交換方式では,鍵$s=s_a=s_b$を共有することが目的でした。エルガマル暗号では,一方からもう一方への暗号化・復号が成立すればOKです。そこで,Diffie Helmanの鍵交換方式で利用された$s=s_a=s_b$の関係をエルガマル暗号でも利用します。

具体的には,AさんからBさんにメッセージ(平文)$m$を送るとき,Aさんは暗号文$M=ms_a$を送ればOKです。Bさんは,復号するには$M÷s_b$をmod $p$の下で行えば$m$が復元されます。
一点だけDiffie Helmanの鍵交換方式と異なるのは,エルガマル暗号は$x$として乱数を利用するということです。乱数を用いることで,強秘匿性(暗号から選択肢の少ない平文を特定できない性質)をもたせることができます。つまり,同じ平文から毎回異なる暗号文が生成されるということです。
一方で,エルガマル暗号は中間者が定数倍の改ざんを行うことができるため,頑強性(元の暗号文から他の暗号文を作ることができない性質)に乏しいです。加えて,エルガマル暗号は「暗号文cを受け取る前後に、自分で選んだc以外の暗号文に対応する平文を得られる」という状況下からの攻撃(CCA2)に対して安全ではないことが知られています。[参考:外部リンク(クラウド時代の暗号化技術論)]
楕円曲線暗号
楕円曲線暗号は,前方秘匿性(PFS:Perfect Forward Secrecy)をもつ鍵共有方式として利用されています。前方秘匿性とは,もし万が一暗号が解読されてしまった時に,通信済みの内容をどの程度守れるかという性質になります。RSA暗号やエルガマル暗号は,前方秘匿性に乏しい暗号です。
あくまでもイメージですが,楕円曲線暗号は浮き輪の表面で演算を行います。modの2次元バージョンのようなものです。特に,浮き輪の形を楕円曲線と呼び,楕円曲線上の離散対数問題(楕円離散対数問題)を根拠に楕円曲線暗号は暗号化されます。
「楕円曲線上の足し算」をもう少し数学的に見てみましょう。楕円曲線は,以下の式で表されます。簡単のために,$a=0$として考えます。
\begin{align}
y^2 &= x^3 + ax^2 + bx + c \; (\rm{mod}\;p)
\end{align}
この曲線上での足し算は,対応する天における接線と楕円曲線の交点$G’$をx軸に関して対照に移動させた点であることを示すことができます。この計算は非常に単純であるため,ある初期値$G$を楕円曲線状で$n$回足し算する計算はすぐに行うことができます。ちなみに,$n$が秘密鍵とされます。
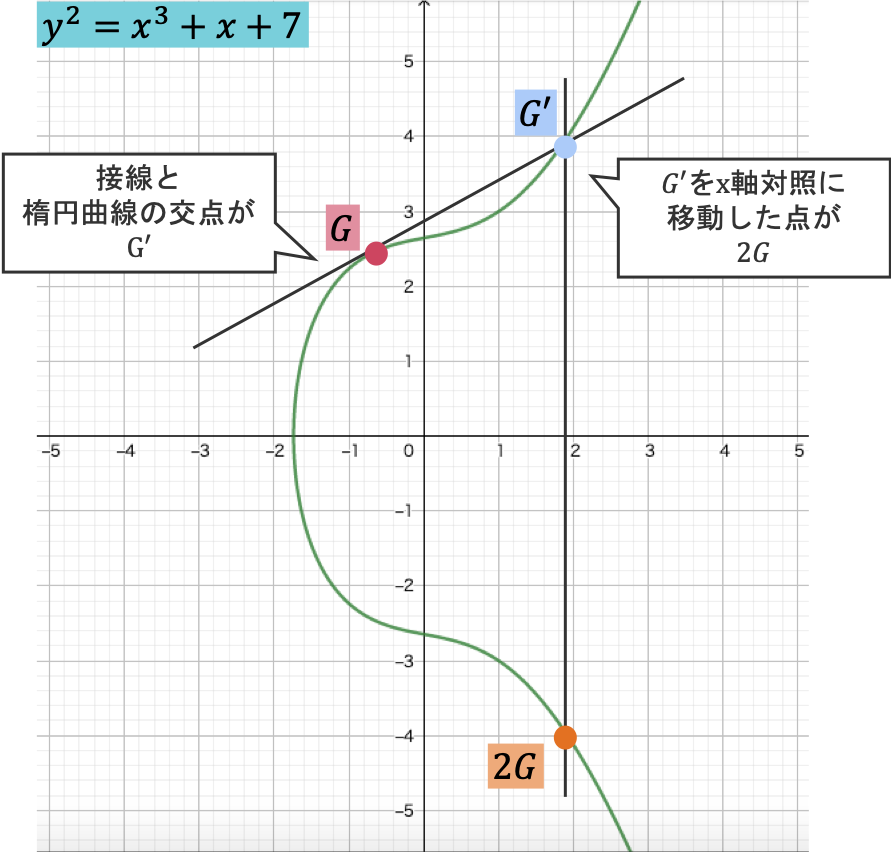
一方,楕円離散対数問題とは,初期値$G$と$G$を$n$回足した$nG$から$n$を求めるのが難しい性質を指しており,RSAなどと同じように,この難しさが一方向関数となり,楕円曲線暗号のキモになっています。
実際のアルゴリズムは以下の通りです。
- 鍵生成:楕円曲線上の点Pを選ぶ。Aは秘密鍵aをランダムに決めて$K_A=aP$を公開鍵とする。
- 暗号化:整数rをランダムに決め、楕円曲線上の点の平文$M$に対して公開鍵$K_A$を使って暗号文$(C_1, C_2)=(rP,M+rK_A)$を作る。
- 復号:暗号文$(C_1, C_2)=(rP,M+rK_A)$を受け取ったAは秘密鍵aを用いて$C_2 – aC_1$で復号する。
準同型暗号
暗号化したまま計算ができる暗号化方式のことを準同型暗号と呼びます。エルガマル暗号が定数倍に弱いという性質は準同型ともいえます。例えば,こちらの記事[外部リンク:クラウド時代の暗号化技術論]でも説明されているように,楕円エルガマル暗号を考えてみます。$M_1$,$M_2$の暗号化は,それぞれ以下の通りです。
\begin{align}
r_1 P, M_1+r_1K_A\\
r_2 P, M_2+r_2K_A
\end{align}
ただし,$r_1$,$r_2$は乱数です。$r’=r_1+r_2$とおくと,それぞれの暗号文を足せば,以下のように表せます。
\begin{align}
(r_1 P, M_1+r_1K_A) + (r_2 P, M_2+r_2K_A) = (r’P, (M_1+M_2)+r’K_A)
\end{align}
この式が何を表しているかというと,「$M_1$の暗号文と$M_2$の暗号文を足したら$M_1+M_2$の暗号文になった!」ということを示しています。このような暗号化方式を加法準同型暗号と呼びます。
IDベース暗号
楕円曲線暗号などでは,公開鍵は楕円曲線上の点として定められました。一方,IDベース暗号では,任意の公開鍵を設定できます。受信者のID(メールアドレス等)から,自動的に公開鍵が誰でも計算できるような仕組みの暗号です。鍵配布が必要ない秘密鍵は,鍵生成機関が作成して本人に渡します。
IDベース暗号は,受信者が秘密鍵を持っていなくても実行することが可能です。一方で,欠点としては,鍵生生成機関が全員の秘密鍵を知っていることになることや,秘密鍵が漏洩してしまった場合にID(メールアドレスなど)を変更しなくてはならないということが挙げられます。
属性ベース暗号
属性ベース暗号は,IDベース暗号においてIDを属性で指定できるような暗号を指しています。例えば,以下のような属性を考えてみましょう。
・情報学研究科のM1
・情報学研究科の教授
・社会情報学専攻のM2又はD3
上記リストの属性が機密情報にアクセスできるものとする方法です。アクセス木などで実現されます。
秘密分散
「n個の異なる点を通るn-1次関数はただ一つに決まる」という性質から,n人に秘密を分散してn-1人集まれば秘密が復元できるという状況を利用する方法が秘密分散です。
代理人再暗号化
準同型暗号を利用すれば,暗号化されたメッセージを他の人が重ねて暗号化することが可能になりますが,現状はまだ実用化には至っていません。そこで,暗号化されたメッセージを,再暗号化鍵を用いて他の人が重ねて暗号化するような方式が考えられました。
代理人は,暗号化だけを行うことができ,暗号文に対応する平文を解読することはできません。この方法は代理人再暗号化と呼ばれており,電子署名や秘密分散などと組み合わせて利用されています。
電子署名
ハッシュ化されたメッセージ$m$に対して,送信者の秘密鍵を利用して暗号化を行うことで,暗号と復号の対称性から,送信者の公開鍵を使えば送信者の正当性が示されます。このような送信者の正当性の示し方を,電子署名と呼びます。
原像攻撃においてハッシュ値が衝突するのに必要な試行回数は$2^n$回に比例します。一方,衝突攻撃においてハッシュ値が衝突するのに必要な試行回数は$2^{\frac{n}{2}}$ に比例し[参考:外部サイト(誕生日攻撃)],意外と少ないです。後者を「誕生日のパラドックス」と呼ぶこともあります。
原像攻撃(弱衝突耐性)は「誕生日が同じ人を1組見つけるために必要な試行回数」に関して,衝突攻撃(強衝突耐性)は「自分と同じ誕生日の人を見つけるために必要な試行回数」に関してです。
公開鍵暗号の安全性が電子署名の安全性を決めます。例えば,RSA暗号によって電子署名を行う場合を考えてみます。
●$M$:メッセージ
●$S$:署名
●$R$:検証結果
●$l_a$:送信者の秘密鍵
●$l_b$:送信者の公開鍵
●$m$:素数の積(送信者の公開鍵)
\begin{eqnarray}
R &=& S^{l_b}\ \rm{mod}\ m \\
S &=& M^{l_a}\ \rm{mod}\ m
\end{eqnarray}
もし,$M$の署名$S$,送信者の公開鍵$l_b$,$m$から$M’^{l_a}\ \rm{mod}\ m=S$となる$M’$を作れてしまったとします。このとき,$M=M^{l_a l_b}\ \rm{mod}\ m$ですので,$M’=M^{l_a}\ \rm{mod}\ m$となります。これは,RSA暗号が解読されたことを意味します。この時点で,電子署名の正当性も崩れてしまいます。(リダクション)
PKI
いくら公開鍵暗号でも,公開鍵が改ざんされてしまえば攻撃者によってなりすましが行われる可能性があります。公開鍵が本人であるという保証が必要になるということです。そこで,「信頼できる公開鍵」扱えるようにした基盤がPKIです。PKIに関しては,以下の記事で詳しくお伝えしています。

特に,ブラウザとDNSサーバの通信を考えたときには,DNSポイズニングによってブラウザ利用者を攻撃者側のサーバに誘導するような攻撃を回避するために,PKIという仕組みを利用しています。