この記事では,研究のサーベイをまとめていきたいと思います。ただし,全ての論文が網羅されている訳ではありません。また,分かりやすいように多少意訳した部分もあります。ですので,参考程度におさめていただければ幸いです。
間違えている箇所がございましたらご指摘ください。随時更新予定です。他のサーベイまとめ記事はコチラのページをご覧ください。
本記事の内容
大学で学習した「情報セキュリティ」の内容を網羅的にまとめていくものです。目次は以下の記事をご覧ください。

暗号と認証の必要性
情報セキュリティ<概要編>でもお伝えした通り,情報セキュリティには3つの要件があります。
【情報セキュリティの3要件】
●機密性(Confidentiality)
●完全性(Integrity)
●可用性(Availability)
その中でも,暗号と認証は機密性を維持するための手法として知られています。機密性とは,アクセスを許可されたものだけが情報を手に入れられることを指します。アクセス権限をまとめたものは,UCL(User Account Control)と呼ばれます。
機密性を確保するためは,最も簡単な方法として認証システムが挙げられます。特定のユーザとそのパスワードを知っている者だけがアクセスできるように設定すればいいのです。
しかし,万が一認証を突破できてしまえば,攻撃者は簡単に情報にアクセスできてしまうのです。その,万が一に備えるための術が,暗号ということになります。
暗号の基礎知識
暗号は,そのいかついネーミングから「安心・安全」のようなイメージを持たれる方も多いのではないかと思います。例えば,Wi-fiのセキュリティアルゴリズムの一つである「WPA」は,通常の無線LAN環境において10秒で解読可能であることが2008年に示されました。(参考:森井昌克 神戸大学大学院教授HP)
他にも,https接続も特定のコードに対して脆弱性が発見されるケースもあります。(“Forbidden attack” makes dozens of HTTPS Visa sites vulnerable to tampering | Ars Technica)
古典暗号
そもそも,暗号とは「通信においてデータが第三者に読まれないようにする手法」のことを指します。以下の記事でも簡単に説明しています。

転置式暗号
平文の文字を並べ替えることで暗号化を施します。例としては,スキュタレー暗号が挙げられます。
【スキュタレー暗号】
●アルゴリズム
棒の周りに沿って文字を書いていく
●暗号鍵
棒の太さ
換字式暗号
文字を置き換えることで暗号化を施します。例としては,シーザー暗号が挙げられます。
【シーザー暗号】
●アルゴリズム
→ある規則に則って文字を置き換える
●暗号鍵
→ある規則
他にも,「バーナム暗号」と呼ばれる換字式の暗号があります。
【バーナム暗号】
●アルゴリズム
→乱数とのXORを取る
●暗号鍵
→平文と同じ長さの乱数
送信者と受信者の間では,あらかじめ平文と同じ長さの乱数が共有されているものとします。送信者は,平文と乱数のXOR(排他的論理和)を取ることで暗号化を施します。受信者も,暗号文と乱数のXORを取ることで複合することができます。以下は簡単な証明です。
・$A$:平文
・$B$:暗号文
・$r$:乱数
まず平文と乱数の排他的論理和を取ることで暗号化します。
\begin{eqnarray}
B = A \oplus r
\end{eqnarray}
次に,暗号文と乱数の排他的論理和を取ることで復号します。
\begin{eqnarray}
B \oplus r = A \oplus r \oplus r = A
\end{eqnarray}
このように,あらかじめ鍵を共有しておく暗号化方式を,共通鍵暗号と呼びます。共通鍵暗号の一種であるバーナム暗号には,いくつかの問題点があります。
第一に,「鍵をどのようにして交換しておくか」が問題になります。鍵を安全に交換するためには,暗号化を施さなくてはなりません。しかし,その暗号化のためには鍵を共有しておく必要があるのです。このように,暗号化と共通鍵の交換は,卵が先か鶏が先かの議論に発展してしまいます。
加えて,バーナム暗号では「同じ長さの乱数をなんども使用していると,その傾向から乱数がバレてしまう危険性がある」という問題点も指摘できます。つまり,鍵を守るコストと平文を守るコストが同じになってしまうため,そもそも暗号化の意味がなくなってしまうということがいえます。
現代暗号
このような古典暗号の問題点を,現代暗号では「暗号化のアルゴリズムを公開すること」で解決していきます。暗号化の仕組みを公開することで,安全性のテストを行うことができます。そのおかげで,私たちは安全性が担保された暗号化方式を利用することができています。
現代暗号は,大きく分けて「共通鍵暗号」と「公開鍵暗号」に分けられます。前者は,さらに固定長のデータを扱う「ブロック暗号」と,ある単位ごとに暗号化を施す「ストリーム暗号」に大別されます。今回お伝えしている手法は,以下のように分別されます。
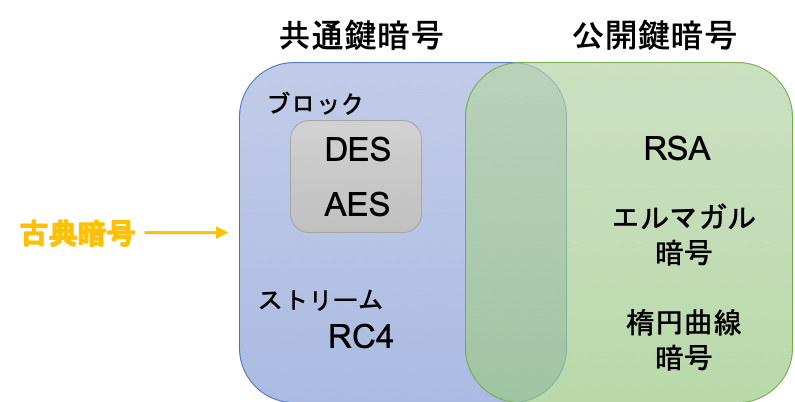 暗号の大別
暗号の大別現代暗号のはじまりは,DES(Data Encryption Standard)が公開された1976年まで遡ります。DESは共通鍵暗号の1つで,共通鍵には56ビットを設けています。しかし,その鍵長が短いために,安全性が担保できず,攻撃法も存在します。
DESはのちにトリプルDESという形で利用されるようになりますが,結局はAES(Advanced Encryption Standard)に代替されるようになります。AESは,「換字表」「シフト」「XOR」を利用したアルゴリズムで,比較的単純な計算に基づいて暗号化を施す手法です。安全性は,DESよりも優れているとされています。
他にも,RC4という共通鍵暗号化が挙げられます。RC4は,ビット単位,またはバイト単位で暗号化を逐次施していく手法です。DESもAESも,固定長のデータに暗号化を施すため,ブロック暗号化に分類されます。一方,RC4は各バイトごとに処理を施すため,ストリーム暗号化に分類されます。
しかし,これらの手法も結局は共通鍵暗号ですので,鍵をどのようにして共有するのかという問題点が残っています。この問題の解決方法としては,以下が挙げられます。
●鍵の事前配布
●鍵配布センターの活用
ここで,数学的な理論を背景とした「Diffie-Hellman鍵交換アルゴリズム」は,共通鍵を共有する手段として発案されました。Diffie-Hellman鍵交換アルゴリズムは,簡単にいえば「素数の割り算の性質を利用した超賢い鍵交換法」です。最初にアルゴリズムを紹介しておきたいと思います。
1.大きな素数$p$と適当な整数$x$を公開
2.送受信者共に適当な正整数$l$($\leq q$)を選ぶ
3.送受信者共に$k = x^a \rm{mod} p$を公開する
4.共通鍵は$s = k^l \rm{mod} p$と設定する
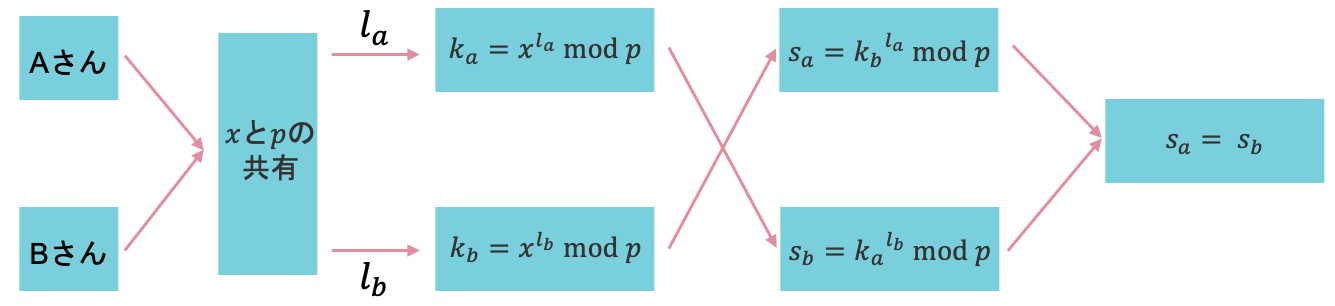
ここでは,なぜDiffie-Hellman鍵交換アルゴリズムが通信の傍受に強いのか,そしてなぜ$s_a = s_b$となるのかについて見ていきたいと思います。
傍受者にとって,Diffie-Hellman鍵交換アルゴリズムを行う通信から得られる情報は,「$x, p, k$」のみです。そして,$k=x^l \rm{mod} p$という計算において,$p$が大きい素数の場合には「$x, p, k$」から「$l_a$」を求めることは非常に困難であることが知られています。
そのため,$l_a$と$l_b$は部外者にはバレない秘密鍵のような存在となることが分かります。これらの自分しか知らない情報を使って計算した$s$が,送受信者間で一致してしまうのです。簡単な証明を以下に示します。
\begin{eqnarray}
s_a &=& k_b^{l_a}\; \rm{mod}\; p \\
&=& x^{l_a l_b}\; \rm{mod}\; p \\
&=& \{x^{l_a}\}^{l_b}\; \rm{mod}\; p \\
&=& k_a^{l_b}\; \rm{mod}\; p \\
&=& s_b
\end{eqnarray}
以上のアルゴリズムを利用すれば,素数の割り算による逆算の難しさを利用して共通鍵を共有することができます。しかし,一方で,送受信者が互いに面識がない場合「中間者攻撃」に耐性がないことも知られています。傍受者は「$x, p, k$」の情報を知ることができますが,同時に改ざんをすることもできます。
つまり,送受信者にバレない形で両方の$k$の改ざんを試みれば,たとえ$l$が分からなくとも,傍受者は,送信者にとって受信者のフリ,受信者にとっての送信者のフリをすることができてしまうのです。
Diffie-Hellman鍵交換アルゴリズムの功績は共通鍵の共有を可能にしたことだけではなく,公開鍵の概念を導入した点にも見られます。たとえ鍵の一部を公開したとしても,素数などの性質を利用して傍受者が鍵を計算できないような仕組みを作り上げれば,暗号化方式として成立することを知らしめました。
このような公開鍵暗号で代表的なものに「RSA暗号」が挙げられます。RSA暗号に関しては,以下の記事で詳しくお伝えしています。

利点欠点
共通鍵暗号は,その速さに利点がある一方で,鍵の共有方法に問題があります。公開鍵暗号は,鍵の管理が容易であり,電子署名への応用も期待できる一方で,1対多通信では通信路の数だけ暗号化が必要となるという欠点が挙げられます。そこで,現在では共通鍵暗号と公開鍵暗号の両方をハイブリットした手法がよく用いられています。(共通鍵の共有を公開鍵暗号化)
まとめ
情報セキュリティの暗号化についてお伝えしました。超基本的な内容にもかかわらず,頭が混乱してしまうような数式も含まれてきています。頭が混乱するくらいだから,暗号化というのかもしれません。