今回は,scikit-learnなどの既成ライブラリにできるだけ頼らずに,主成分分析とフィッシャーの線形判別分析法の基本的な違いを確認していこうと思います。また,本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。
読みたい場所へジャンプ!
主成分分析
こちらの記事で詳しく説明しています。

フィッシャーの線形判別分析
こちらの記事で詳しく解説しています。

必要なモジュールのインポート
import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt
cm = plt.get_cmap("tab10")数値計算のためのnumpy,(行列計算のためのlinalg),グラフ出力のためのpyplot,配色をするためのc_mapをインポートします。
データの生成
m1 = np.array([10, 5])
s1 = np.array([[1, 2], [2, 5]])
m2 = np.array([1, 3])
s2 = np.array([[1, 2], [2, 5]])
N = 100
x1 = np.random.multivariate_normal(m1, s1, N)
x2 = np.random.multivariate_normal(m2, s2, N)
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.show()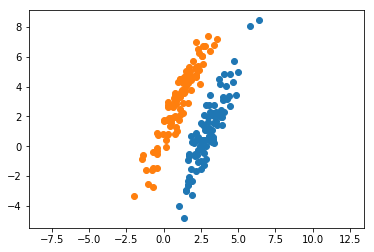 numpyのmultivariate_normalを利用して,適当な平均と共分散行列からデータを生成しておきます。以下では,これらのデータとクラスが「与えられたもの」とします。主成分分析は,すべてのクラスを同一視して1つの軸(主成分)を抽出します。フィッシャーの判別分析では,データが属するクラスを既知として軸を求めにいきます。
numpyのmultivariate_normalを利用して,適当な平均と共分散行列からデータを生成しておきます。以下では,これらのデータとクラスが「与えられたもの」とします。主成分分析は,すべてのクラスを同一視して1つの軸(主成分)を抽出します。フィッシャーの判別分析では,データが属するクラスを既知として軸を求めにいきます。
主成分分析の変換行列
[eig, u] = eigsort(S)上でお伝えしたコチラの記事の関数を利用すれば,上記コードのuが主成分分析における変換行列になります。
フィッシャーの線形判別分析法の変換行列
w = LA.inv(cal_sw(x1, m1, x2, m2)) @ (m2 - m1)こちらは,単純にフィッシャーの基準に沿ったパラメータを計算しているだけです。こちらのwがフィッシャーの線形判別分析法の変換行列になります。
射影を行う
z_pca = x @ u
w *= -1
z1_fisher = x1 @ w
z2_fisher = x2 @ w両方の手法とも,線形基底を考えているため変換行列をオリジナルのデータにかけ合わせることで射影後のデータを取得できます。特に,フィッシャーの判別基準で得られたwは主成分分析の軸の向きと反対になっていたため,-1をかけることで向きを合わせています。
ヒストグラム表示
plt.hist(z_pca[:N-1,0], alpha=0.7, color=cm(0))
plt.hist(z_pca[N:,0], alpha=0.7, color=cm(1))
plt.hist(z1_fisher, alpha=0.7, color=cm(0))
plt.hist(z2_fisher, alpha=0.7, color=cm(1))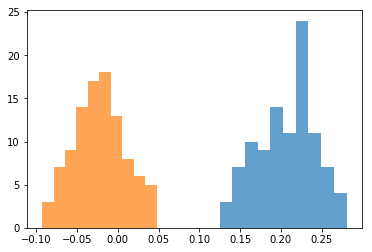
考察
PCAは特徴量抽出,フィッシャーの判別分析法は分類という用途が現れた結果となりました。主成分分析では,2つのクラスを分離する信念はないため,大部分が重なり合っている結果になりました。しかし,両方ともヒストグラムの裾が広く,フィッシャーの基準による結果よりも各クラスのデータをより詳しく表せていることが分かります。
一方,フィッシャーの基準によるヒストグラムでは,2つのクラスがきれいに分かれています。しかし,フィッシャーの判別分析には各クラスのデータの特徴量を保とうという信念がないため,データがつぶれてしまっていて情報が抜け落ちてしまっています。
正直なところ,特徴量抽出と分類という用途の違いは明確に表れたものの,特徴量を保持しているかどうかという点に関しては,フィッシャーの基準によるヒストグラムでもよく保持しているように見えます。これは,次元が少ないから各手法の違いが明確になっていないだけで,より多くの次元を扱うようになれば,両者の違いはよりハッキリしてくるのだと思います。
もし理論にモヤモヤがあれば
(2026/02/20 02:48:42時点 楽天市場調べ-詳細)
こちらの参考書は,PRMLよりも平易に機械学習全般の手法について解説しています。おすすめの1冊になりますので,ぜひお手に取って確認してみてください。
全コード
import numpy as np
import matplotlib.pyplot as plt
cm = plt.get_cmap("tab10")
m1 = np.array([3, 1])
s1 = np.array([[1, 2], [2, 5]])
m2 = np.array([1, 3])
s2 = np.array([[1, 2], [2, 5]])
N = 100
x1 = np.random.multivariate_normal(m1, s1, N)
x2 = np.random.multivariate_normal(m2, s2, N)
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.show()
def eigsort(S):
eigv_raw, u_raw = LA.eig(S)
eigv_index = np.argsort(eigv_raw)[::-1]
eigv = eigv_raw[eigv_index]
u = u_raw[:, eigv_index]
return [eigv, u]
x = np.concatenate([x1,x2])
m = np.mean(x, axis=0)
S = (1/x.shape[0]) * ((x - m).T @ (x - m))
[eig, u] = eigsort(S)
xlist = np.arange(-5,7.5,0.1)
ylist = m[1] + (u[[1],[0]]/u[[0],[0]]) * (xlist - m[0])
plt.plot(xlist, ylist, color=cm(2))
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.ylim(-6,10)
plt.show()
contribution = round(eig[0]/(eig[0]+eig[1])*100, 1)
print("The first contribution:" + str(contribution)+"%")
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(x)
PCA(n_components=2)
ytest = m[1] + (pca.components_[[0],[1]]/pca.components_[[0],[0]]) * (xlist - m[0])
fig = plt.figure()
plt.plot(xlist, ytest, color=cm(3))
plt.plot(x1[:,0], x1[:,1], 'o')
plt.plot(x2[:,0], x2[:,1], 'o')
plt.axis('equal')
plt.ylim(-6,12)
plt.show()
print("\n"*5) #adjust for pdf
contribution2 = pca.explained_variance_ratio_[0]*100
print("The first contribution:"+ str(contribution2)+"%")
def cal_sw(x1, m1, x2, m2):
sw = ((x1 - m1).T @ (x1 - m1)) + ((x2 - m2).T @ (x2 - m2))
return sw
w = LA.inv(cal_sw(x1, m1, x2, m2)) @ (m2 - m1)
xlist = np.arange(-5,10,0.1)
ylist = m[1] + (w[1]/w[0]) * (xlist - m[0])
ydisc = m[1] + (-w[0]/w[1]) * (xlist - m[0])
plt.plot(xlist, ylist, color=cm(4))
plt.plot(xlist, ydisc, linestyle='dashed', color='black')
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.ylim(-6,12)
plt.show()
z_pca = x @ u
w *= -1
z1_fisher = x1 @ w
z2_fisher = x2 @ w
plt.hist(z_pca[:N-1,0], alpha=0.7, color=cm(0))
plt.hist(z_pca[N:,0], alpha=0.7, color=cm(1))
plt.hist(z1_fisher, alpha=0.7, color=cm(0))
plt.hist(z2_fisher, alpha=0.7, color=cm(1))















