【超初心者向け】主成分分析(PCA)をpythonで実装してみた。

 

今回は，scikit-learnなどの既成ライブラリにできるだけ頼らずに，主成分分析の基本的な部分を実装していこうと思います。また，本記事はpython実践講座シリーズの内容になります。その他の記事は，こちらの「Python入門講座/実践講座まとめ」をご覧ください。

必要なモジュールのインポート

import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt
cm = plt.get_cmap("tab10")

数値計算のためのnumpy，(行列計算のためのlinalg)，グラフ出力のためのpyplot，配色をするためのc_mapをインポートします。

 

データの生成

m1 = np.array([10, 5])
s1 = np.array([[1, 2], [2, 5]])
m2 = np.array([1, 3])
s2 = np.array([[1, 2], [2, 5]])

N = 100

x1 = np.random.multivariate_normal(m1, s1, N)
x2 = np.random.multivariate_normal(m2, s2, N)
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.show()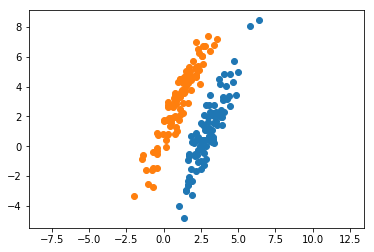

numpyのmultivariate_normalを利用して，適当な平均と共分散行列からデータを生成しておきます。以下では，これらのデータが「与えられたもの」として主成分分析を施していきます。特に，今回は２つのクラスを同一視して主成分分析を施すことで，別記事でFisherの線形判別分析法との比較を行っていきたいと思います。

 

固有ベクトルを固有値の大きい順に並べる関数

def eigsort(S):
  eigv_raw, u_raw = LA.eig(S)
  eigv_index = np.argsort(eigv_raw)[::-1]
  eigv = eigv_raw[eigv_index]
  u = u_raw[:, eigv_index]
  return [eigv, u]

主成分分析では，射影先の軸が固有ベクトルに対応します。そして，主成分分析の目的が元のデータをよく表すような射影をして次元を下げることなので，出来るだけ元の特徴をよく表す軸を選びます。このとき，数式上で確認すれば，固有値の大きさがもとの特徴を表す大きさと同一視できることが分かります。ですので，固有ベクトルを固有値の大きい順に並べることで，変換後の主成分（射影後に選ばれたデータ）を整理して保持することができます。

コードのポイントとしては，[::-1]で降順ソートになる点，リストのインデックス指定にインデックスリスト（リストの中身がインデックスを表しているもの）が利用できる点，そしてlinalgで求めた固有ベクトルは縦ベクトルであるために[:, eigv_index]で縦ベクトルをインデックス順に並び替えている点です。

 

２つのデータを同一視

x = np.concatenate([x1,x2])
m = np.mean(x, axis=0)
S = (1/x.shape[0]) * ((x - m).T @ (x - m))

x1とx2の２つのクラスを同一視していきます。同一視したxに対して，平均と共分散行列を求めます。このように，主成分分析はそれぞれのデータが属するクラスを知らない場合でも行うことができます。

 

ソートされた固有値と固有ベクトルを求める

[eig, u] = eigsort(S)

先ほど定義した関数を利用して，データ全体の共分散行列の固有値と固有ベクトルを求めます。

 

グラフ描写の準備

xlist = np.arange(-5,7.5,0.1)
ylist = m[1] + (u[[1],[0]]/u[[0],[0]]) * (xlist - m[0])

グラフのx軸は適当に生成します。それぞれのxに対応するyは，傾きが「固有ベクトルをまとめた行列であるuの」「第１列の」「（yの増加量）/（xの増加量）」で，データ平均を通るように設定します。

 

グラフ描写

plt.plot(xlist, ylist, color=cm(2))
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.ylim(-6,10)
plt.show()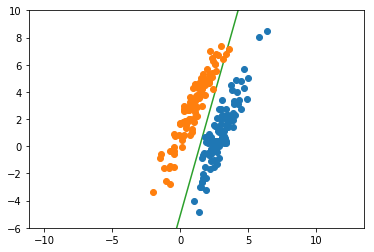

分散が大きくなるような方向に軸が設定されていることが分かります。

 

寄与率の計算

contribution = round(eig[0]/(eig[0]+eig[1])*100, 1)
print("The first contribution:" + str(contribution)+"%")

（出力）
The first contribution:79.2%

寄与率は，全固有値のうち選択している固有値がどのくらいの割合を占めているかを表す数値です。今回は2次元ですので，第2主成分の寄与率は100-79.2=20.8%になります。

 

既成ライブラリとの比較

from sklearn.decomposition import PCA

# ライブラリを使用してPCA
pca = PCA(n_components=2)
pca.fit(x)
PCA(n_components=2)

# ライブラリの出力から直線を表示
ytest = m[1] + (pca.components_[[0],[1]]/pca.components_[[0],[0]]) * (xlist - m[0])

# グラフ出力の準備
fig = plt.figure()
plt.plot(xlist, ytest, color=cm(3))
plt.plot(x1[:,0], x1[:,1], 'o')
plt.plot(x2[:,0], x2[:,1], 'o')
plt.axis('equal')
plt.ylim(-6,12)
plt.show()

# 寄与率の計算
contribution2 = round(pca.explained_variance_ratio_[0]*100, 1)
print("The first contribution:"+ str(contribution2) + "%")

（出力）
The first contribution:79.2%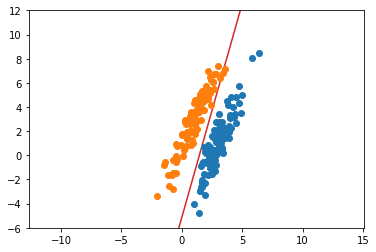

先ほどと同じような結果になりました。

 

考察

よく言われることですが，PCAは次元削減のための道具です。そのためには，寄与率という指標を利用しながら選択する主成分を吟味する必要があります。今回のような二次元のデータであれば，いちいちeigsortなどという関数を定義する必要はありませんが，多次元に拡張する場合は関数にまとめることで見通しよく主成分分析を行えることが見込めます。

しかし，ライブラリの威力は凄まじいですね…。たった3行でPCAが完了してしまうのですから，実践ではライブラリを使わない手はないでしょう。別記事で，Fisherの線形判別分析法との比較をしていますので，よろしければご参照ください。

 

もし理論にモヤモヤがあれば

こちらの参考書は，誰もが挫折しかけるPRMLよりも平易に機械学習全般の手法について解説しています。おすすめの１冊になりますので，ぜひお手に取って確認してみてください。

 

全コード

import numpy as np
import matplotlib.pyplot as plt
cm = plt.get_cmap("tab10")

m1 = np.array([3, 1])
s1 = np.array([[1, 2], [2, 5]])
m2 = np.array([1, 3])
s2 = np.array([[1, 2], [2, 5]])

N = 100

x1 = np.random.multivariate_normal(m1, s1, N)
x2 = np.random.multivariate_normal(m2, s2, N)
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.show()
​
def eigsort(S):
  eigv_raw, u_raw = LA.eig(S)
  eigv_index = np.argsort(eigv_raw)[::-1]
  eigv = eigv_raw[eigv_index]
  u = u_raw[:, eigv_index]
  return [eigv, u]

x = np.concatenate([x1,x2])
m = np.mean(x, axis=0)
S = (1/x.shape[0]) * ((x - m).T @ (x - m))

[eig, u] = eigsort(S)

xlist = np.arange(-5,7.5,0.1)
ylist = m[1] + (u[[1],[0]]/u[[0],[0]]) * (xlist - m[0])

plt.plot(xlist, ylist, color=cm(2))
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.ylim(-6,10)
plt.show()
contribution = round(eig[0]/(eig[0]+eig[1])*100, 1)
print("The first contribution:" + str(contribution)+"%")

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(x)
PCA(n_components=2)
ytest = m[1] + (pca.components_[[0],[1]]/pca.components_[[0],[0]]) * (xlist - m[0])
​
fig = plt.figure()
plt.plot(xlist, ytest, color=cm(3))
plt.plot(x1[:,0], x1[:,1], 'o')
plt.plot(x2[:,0], x2[:,1], 'o')
plt.axis('equal')
plt.ylim(-6,12)
plt.show()
contribution2 = pca.explained_variance_ratio_[0]*100
print("The first contribution:"+ str(contribution2)+"%")