この記事では,研究のサーベイをまとめていきたいと思います。ただし,全ての論文が網羅されている訳ではありません。また,分かりやすいように多少意訳した部分もあります。ですので,参考程度におさめていただければ幸いです。間違えている箇所がございましたらご指摘ください。随時更新予定です。
他の研究関連記事はこちらから。

三者の概要
非負値行列因子分解(NMF; Non-negative Matrix Factorization),主成分分析(PCA; Principal Component Analysis),独立成分分析(ICA; Independent Component Analysis)は,いずれも行列因子分解に基づいて定式化されます。NMFやICAは音源分離,PCAは次元削減の手法として利用されることが多いです。
この記事では,三つの手法を統一的な観点から比べてきます。そのためには,いずれも行列の積に分解しているという出発点から話を始める必要があります。少し確認してみましょう。
$$
\newcommand{\mA}{\mathbf{A}}
\newcommand{\mH}{\mathbf{H}}
\newcommand{\mS}{\mathbf{S}}
\newcommand{\mW}{\mathbf{W}}
\newcommand{\mI}{\mathbf{I}}
\newcommand{\mX}{\mathbf{X}}
\newcommand{\mY}{\mathbf{Y}}
\newcommand{\vs}{\mathbf{s}}
\newcommand{\vw}{\mathbf{w}}
\newcommand{\vx}{\mathbf{x}}
$$
NMF
NMFはある非負値行列を2つの非負値行列の積で表そうとする手法です。
\begin{align}
\mathbf{X} &= \mathbf{W}\mathbf{H}
\end{align}
ただし,$\mX\in{\mathbb R}+^{F\times T}$,$\mW\in{\mathbb R}+^{F\times K}$,$\mH\in{\mathbb R}_+^{K\times T}$です。
PCA・ICA
先にタネあかしをすると,ICAはPCAの拡張です。逆に言えば,PCAはICAの特別な場合に相当します。ですので,基本的にPCAとICAは同じ行列分解にしたがって定式化が行われます。
ICAは音源分離などに利用される手法であり,出発点となる行列分解には二つの方法があります。以下の二つのモデルを駆使しながら定式化が行われます。イメージとしては,$\mathbf{x}$は混合音源,$\mathbf{s}$は音源,$\mathbf{A}$は各音源がどのように混合されるかを表す行列です。また,$\mathbf{W}$は$\mathbf{x}$をどのように各音源に分離するかを表す行列です。
混合モデル
\begin{align}
\mathbf{x}_{f t} &= \mathbf{A}_{f} \mathbf{s}_{f t}\\
&= \sum_{n=1}^N \mathbf{a}_{nf} \mathbf{s}_{n f t}
\end{align}
分離モデル
\begin{align}
\mathbf{s}_{f t} &= \mathbf{W}_{f} \mathbf{x}_{f t}\\
&= \sum_{m=1}^M \mathbf{w}_{m f} \mathbf{x}_{m f t}
\end{align}
ただし,$\mA_f \in {\mathbb R}^{(M \times N)}$,$\mW_f \in {\mathbb R}^{(N \times M)}$です。
定式化
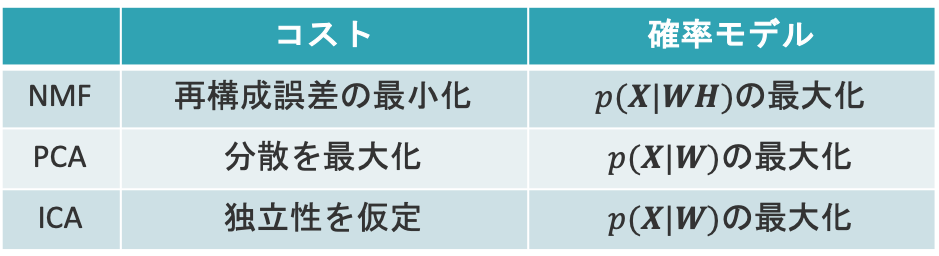
三つのモデルは,それぞれ「コスト関数に基づく方法」と「尤度関数に基づく方法」によって定式化されます。これらは,対照的なアプローチです。
例えば,最小二乗法の場合,「コスト関数に基づく方法」では,説明変数と目的変数の二乗誤差に基づいて目的変数を定めていきます。一方,「尤度関数に基づく方法」では,両者の誤差に分散が等しいガウス分布を仮定して,最尤推定を用いて説明変数を定めていきます。
前者は,基本的にコスト関数の最小化で表されるのに対して,後者は尤度関数の最大化で表されることから,対照的なアプローチであるといえます。これらを踏まえて,上で示した三つのモデルの定式化の概要を見てみましょう。
NMFのコスト関数に基づく方法では,元の行列$\mX$と因子分解された行列$\mW\mH$との再構成誤差を最小化することで定式化が行われます。ただし,各行列は非負値を取ることに注意しましょう。NMFの尤度関数に基づく方法では,$\mX$の生成モデルを仮定して最尤推定を行うことで定式化が行われます。
PCAのコスト関数に基づく方法では,行列$\mW$を変換行列と捉え,変換後のデータの分散が最大になるように定式化が行われます。PCAの尤度関数に基づく方法では,NMFと同様に$\mX$の生成モデルを仮定して最尤推定を行うことで定式化が行われます。
ICAは,PCAを拡張した手法であり,変換後のデータに独立性を仮定します。PCAはICAの特別な(非ガウス性を排除した)場合に相当します。これは,ガウス分布を仮定した場合に相関が0であることと独立であることは等価になるためです。
NMF
ここからは,NMFの定式化についてお伝えしていきます。まずは,コスト関数に基づく方法ですが,行列因子分解により計算される再構成データ$\mW\mH$と分解前の行列$\mX$の距離(擬距離を含む)が,コスト関数${\cal C}_{NMF}$として定義されます。ただし,$\mX\in{\mathbb R}_{+}^{F\times T}$,$\mW\in{\mathbb R}_{+}^{F\times K}$,$\mH\in{\mathbb R}_{+}^{K\times T}$です。
\begin{align}
{\cal C}_{NMF} &= {\cal D}(\mX|\mW\mH)
\end{align}
距離関数${\cal D}$には,例えば二乗誤差やKLダイバージェンス,板倉-斎藤疑距離などが用いられます。詳しくは,以下の記事をご覧ください。

次に,生成モデルに基づく方法です。上の記事にもある通り,$P(\mX|\mW\mH)$に正規分布を仮定したとき,コスト関数に二乗誤差を仮定した場合と等価になります。他にも,ポアソン分布を仮定したときはKLダイバージェンス,指数分布を仮定したときには板倉-斎藤疑距離を仮定した場合と等価になる.ここでは,ポアソン分布とKLダイバージェンスの対応について確認していきましょう。
$\mW\mH=\mY$とおくと,$\mX=\mY$のときに対数尤度が最大となることを利用することで,両者が対応していることが説明できます。ポアソン分布の定義は以下の通りです。ただし,$\mX \geq 0$です。
\begin{align}
\mathrm{Poisson}(\mX| \mY) &= \frac{\mY^\mX e^{- \mY}}{\mX!}
\end{align}
両辺の対数を取ることで,$\mX$に関して最大化すべき$L_{P}$を得ます。
\begin{align}
\mathrm{L}_{P}(\mX) &= \log p(\mY|\mX)\\
&= \log \frac{\mX^\mY e^{- \mX}}{\mY!}\\
&= \mY \log \mX – \mX – \log \mY!
\end{align}
$L_P$を$\mX$で偏微分すると,$\mX=\mY$のとき$L_P$は最大となることが分かります。つまり,以下が成立します。
\begin{align} L_p(\mY) – L_p(\mX) \geq 0 \end{align}
この式は,「$L_p(\mY) – L_p(\mX)$」が$\mX$と$\mY$の近さを表す非負値を値域にとる関数であることを示しています。実際に,$L_p(\mY) – L_p(\mX)$を計算すると,KLダイバージェンスの定義式と一致することが確認できます。
\begin{align} L_p(\mY) – L_p(\mX) &= (\mY \log \mY – \mY – \log \mY!) – (\mY \log \mX – \mX – \log \mY!)\\
&= \mY \log \frac{\mY}{\mX} – \mY + \mX\\
&= \mathcal{D}_{KL}(\mY|\mX)
\end{align}
PCA
PCAのコスト関数は,変換後のデータの分散が最大になり,かつ直交するという基準に基づいて定められます。第一主成分$s_{ft1}$の分散は,以下のようにして求められます。
\begin{align}
\mathbb{E}\left[s_{f t 1} s_{f t 1}\right]
&=\mathbf{w}_{f 1}^{\mathrm{T}} \mathbb{E}\left[\mathbf{x}_{f t} \mathbf{x}_{f t}^{\mathrm{T}}\right] \mathbf{w}_{f 1}\\
&=\mathbf{w}_{f 1}^{\mathrm{T}} \mathbf{R}_{f} \mathbf{w}_{f 1}
\end{align}
解を定めるためには,$\left|\mathbf{w}_{f 1}\right|=1$という条件が必要です。ラグランジュの未定乗数法より,第一主成分$s_{ft1}$に対するコスト関数は,以下のように定められます。
\begin{align}
{\cal C}_{PCA}^{(1)} &= \mathbf{w}_{f 1}^{\mathrm{T}} \mathbf{R}_{f} \mathbf{w}_{f 1} + \lambda_{f 1}\left(1-\mathbf{w}_{f 1}^{\mathrm{T}} \mathbf{w}_{f 1}\right)
\end{align}
ただし,$\mathbf{R}_{f}$は$\vx_{ft}$の共分散行列を表します。第二主成分以降の第$i$成分$(i=2,3,\cdots,D)$も同様にコスト関数を定めることができますが,第$i-1$主成分と直交するという条件が必要となる点に注意が必要です。また,主成分分析では次元削減が主に行われるため,$D<N$と設定することが多いようです。
\begin{align}
{\cal C}_{PCA}^{(i)} &= \mathbf{w}_{f i}^{\mathrm{T}} \mathbf{R}_{f} \mathbf{w}_{f i} + \lambda_{f i}\left(1-\mathbf{w}_{f i}^{\mathrm{T}} \mathbf{w}_{f i}\right)
\end{align}
このコスト関数を最大化する$\mathbf{w}_{f i}$を,$\mathbf{w}_{f i-1}$までの主成分と直交するという条件下で求めていくと,$\lambda_{f i}$が$\mathbf{R}_{f}$の固有値,$\vw{f i}$が固有ベクトルに対応していることが確認できます。
PythonでのPCAの実装例は以下をご覧ください。


次に,尤度関数に基づく方法です。ここでは,混合モデルに従って定式化します。今一度,混合モデルの行列分解を確認しましょう。
\begin{align}
\vx_{f t} &= \mA_f \vs_{f t}
\end{align}
ここで,以下の生成モデルを仮定します。
\begin{align}
\vx_{f t} &\sim {\mathcal N}(\mA_{f}\vs_{f t}, \sigma_{f t}^2 \mI)\\
\vs_{f t} &\sim {\mathcal N}(\bf{0}, \mI)
\end{align}
尤度関数に基づく方法では,$p(\vx_{f t}|\mA_{f})$を最大にする$\mA_{f}$を求めます。
\begin{align}
p(\vx_{f t}|\mA_{f}) &= \int_{\vs_{f t}} {\mathcal N}(\mA\vs_{f t}, \sigma_{f t}^2 \mI){\mathcal N}(\bf{0}, \mI) d\vs_{f t}\\
&= {\mathcal N}(\bf{0}, \mA_{f}\mA_{f}^T + \sigma_{f t}^2 \mI)
\end{align}
両辺の対数を取って最大化問題を解けば,コスト関数に基づく方法同様に固有値問題に帰着することが確認できます。
ICA
ICAは,PCAの拡張です。ICAでは,$\vs_{f t}$の各要素$[\vs_{ft1}, \vs_{ft2}, \cdots, \vs_{ftN}]^T$が独立になるように$\vs_{ft}$を定めます。
\begin{align}
p(\vs_{ft}) &= \prod_{n=1}^N p(s_{ftn})
\end{align}
これはつまり,以下のKLダイバージェンス(ICAのコスト関数に相当)を最小化するように$\vs_{ft}$を定める問題と捉えることができます。
\begin{align}
\mathcal{D}_{KL} \left( p(\vs{ft})\middle|\prod_{n=1}^{N}p(\vs_{ftn}) \right)
&= \int p(\vs_{ft}) \log \frac{p(\vs_{ft})}{\prod_{n}p(\vs_{ftn})} d\vs_{ft}\\
&= \int p(\vs_{ft}) \log p(\vs_{ft}) d\vs_{ft} – \sum_{n} \int p(\vs_{ftn}) \log p(\vs_{ft})d \vs_{ft}\\
&= -H(\vs_{ft}) + \sum_{n} H(\vs_{ft})
\end{align}
ただし,$H(\cdot)$はエントロピーを表します。ここで,分離モデル$\mathbf{s}_{f t} = \mathbf{W}_{f} \mathbf{x}_{f t}$を用います。ヤコビアンの関係式から,以下の関係が成立します。
\begin{align}
p(\vx_{ft}) &= \det|\mW_{f}|p(\vs_{ft}) \label{jacobian}
\end{align}
このとき,$\vs_{ft}$のエントロピー$H(\vs_{ft})$は以下のように表されます。
\begin{align}
H(\vs_{ft}) &= \int p(\vs_{ft}) \log p(\vs_{ft}) d\vs_{ft}\\
&= \int \det|\mW_{f}|^{-1} p(\vx_{ft}) \log \left( \det|\mW_{f}|^{-1}p(\vx_{ft}) \right) \det|\mW_{f}|d\vx_{ft}\\
&= H(\vx_{ft}) – \log \left( \det|\mW_{f}| \right)
\end{align}
以上より,ICAの最小化すべきコスト関数は以下のように表されます。
\begin{align}
{\cal C}_{ICA}^{(f)} &= \sum{n}H(\vs_{ftn}) – H(\vx_{ft}) + \log\det|\mW_{f}|
\end{align}
このコスト関数を最小化する$\mW_{f}$は,自然勾配アルゴリズムなどを用いて求められます。次に,尤度関数に基づく方法です。先ほどと同様に,$\vs_{ft}=\mW_f\vx_{ft}$の関係から,式($\ref{jacobian}$)が成り立ちます。
$G(\vx)=-\log p(\vx)$とおくと,ICAの尤度関数は以下のように求められます。
\begin{align}
\log p(\mathbf{X} | \mathbf{W})
&=\log \left( \prod_{f=1}^{F} \prod_{t=1}^{T} p\left(\mathbf{x}_{f t} | \mathbf{W}_{f}\right) \right)\\
&= \log \left( \prod_{f=1}^{F} \prod_{t=1}^{T}\left|\operatorname{det}\left(\mathbf{W}_{f}\right)\right| \prod{n=1}^{N} p\left( \vs_{f t} \right) \right)\\
&= \log \left( \prod_{f=1}^{F} \prod_{t=1}^{T}\left|\operatorname{det}\left(\mathbf{W}_{f}\right)\right| \prod{n=1}^{N} p\left( \mathbf{w}_{f n}^{\mathrm{H}} \mathbf{x}_{f t} \right) \right)\\
&= T \sum_{f=1}^{F}\log \left|\operatorname{det}\left(\mathbf{W}_{f}\right)\right| – \sum{f=1}^{F} \sum_{t=1}^{T} \sum_{n=1}^{N} G\left(\mathbf{w}_{f n}^{\mathrm{H}} \mathbf{x}_{f t}\right)
\end{align}
いくつかのWeb上の資料とは異なる結果かもしれません。これは,本記事ではヤコビアンの関係式($\ref{jacobian}$)で$\mW \in {\mathbb R}^{N \times M}$を仮定しているためです。複素数を仮定した場合には,ヤコビアンの関係式が異なります。なお,得られた尤度関数は,補助関数法(MMアルゴリズム)等を用いて最大化されます。
共通点・相違点
三者の共通点として,情報の抽出機構として機能するという点が挙げられます。NMFでは,適切な基底行列を与えた場合には,各基底に対応するアクティベーション行列が得られます。逆に,適切なアクティベーション行列を与えた場合には,各アクティベーションに対応する基底行列が得られます。
PCAでは,正規直交基底上への射影を前提として,射影後のデータの分散が最も大きい,つまりデータが極端に散らばって各データのもつ情報量が大きくなるような成分を抽出します。これは,変換後のデータが無相関になるような基底行列を抽出しているとも捉えられます。
ICAでは,各成分が独立になるような成分を抽出しています。独立は無相関の必要条件であるため,ICAはPCAよりも「厳しい」基準で成分を抽出していると捉えられます。音源分離などの問題設定では,各音源が独立であるという仮定に十分な妥当性が考えられるため,ICAは適している手法であると考えられます。
次に,相違点をお伝えします。NMFは元の行列をいかに再構成できるかという基準に基づく一方で,PCAとICAは基本的に分解する行列因子の次元を削減することが多いです。PCAは高次元のデータの性質を効率よく表する目的で利用されることが多く,ICAは混合データを独立な成分に分離する目的で利用されることが多いです。
また,PCAはICAの特別な場合です。ICAを「白色化」「回転」というレイヤーに分割した場合に,PCAは白色化の操作に相当します。また,非ガウス性という条件を排除した場合に,PCAとICAは等価になります。NMFでは対象の行列を非負値で仮定していますが,複素NMFを利用すれば,複素数に対して行列分解が可能になります。複素NMFに関しては,以下の記事をご覧ください。

NMFは混合モデルで定式化されるのに対し,PCAとICAは分離モデルで定式化されるという違いも挙げられます。一般に,ブラインド音源分離の分野では,優決定条件(音源数$\leq$チャネル数)の場合にはICA,劣決定条件(音源数$\geq$チャネル数)の場合にはNMFが利用されることが多いです。















