この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多少意訳した部分もあります。ですので，参考程度におさめていただければ幸いです。間違えている箇所がございましたらご指摘ください。随時更新予定です。
NMFに関して
NMFの更新式の導出はコチラをご覧ください。
NMFと最尤推定の関係についてはコチラをご覧ください。
３種類の距離関数（乖離度）
NMF（非負値行列因子分解）で、モデル化した行列の積と観測データ行列の「数学的な近さ」を測る指標として、主に３種類の距離（乖離度）が用いられています。
「数学的な距離」
●ユークリッド距離（二乗距離）
●Iダイバージェンス
●板倉斎藤擬距離
（ISダイバージェンス）
上から順番に、定義は以下の通りです。
\mathcal{D}_{EU}(y|x) &=& (y – x)^2\\
\mathcal{D}_{KL}(y|x) &=& y\log\frac{y}{x} – y + x\\
\mathcal{D}_{IS}(y|x) &=& \frac{y}{x} – \log\frac{y}{x} – 1\\
\end{eqnarray}
以下では、３種類の距離にどのような性質があるか比べていきたいと思います。
グラフで可視化
まずは$y = 1$として固定して、それぞれの乖離度を$x$の関数と見たときにどのようなふるまいをするのか観察してみましょう。
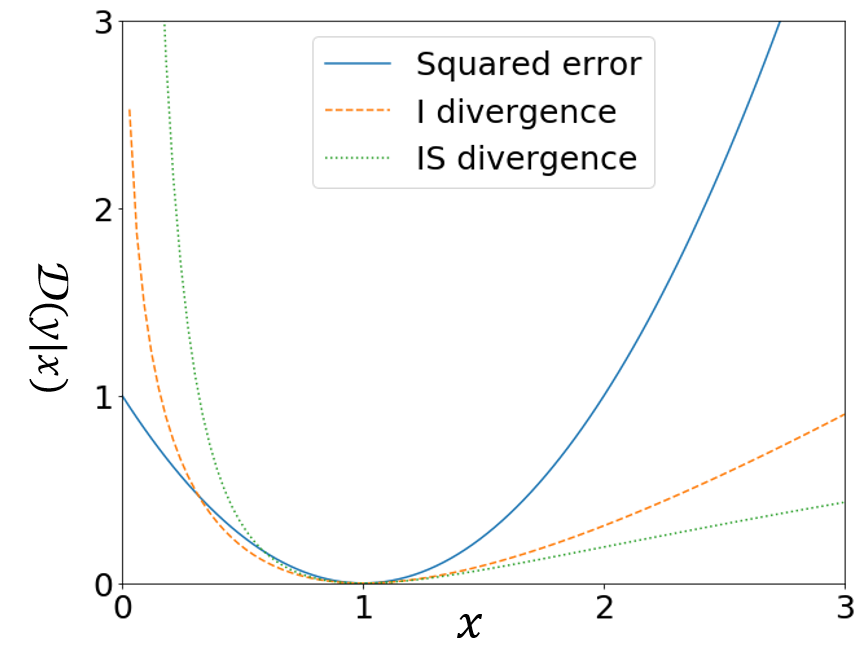各乖離度の比較
性質考察
まず読み取れるのは、ユークリッド距離が$x = 1$を軸にして対象であるという点です。一方、IダイバージェンスとISダイバージェンスは$x = 1$を軸にして非対称であり、両者とも$x$が$x = 1$を大きく下回る場合により大きな値を取ることが分かります。
さらに、定義式（3）からも分かる通り、ISダイバージェンスは$y$と$x$の比だけで表される関数であるため、スケールに依存しません。具体的には、音楽や音声のパワーは低域が高く、高域は低いのですが、ISダイバージェンス基準であれば両者を同等の重要度で扱うことができます。
実際の応用
それでは、実際にはどのような形で乖離度の関数を選択しているのでしょうか。これは現在、観測信号の生成モデルの仮定によって判断しているという状況です。具体的は、観測パワースペクトルの加法性が仮定できる場合にはISダイバージェンス、観測振幅スペクトルの加法性が仮定できる場合にはIダイバージェンスを利用します。ただし、後者は物理的に意味を持たないモデルを仮定していることに注意しましょう。
しかし、それにも関わらず、Iダイバージェンス基準の方が良い結果を与えることが示されています。（以下の論文より）
●「On the use of the beta divergence for musical source separation」（ D. FitzGerald/M. Cranitch/E. Coyle,2009,ISSC）
●「Optimal cost function and magnitude power for NMF-based speech separation and music interpolation（B.King/C.Févotte,P.Smaragdis,2012,IEEE）
●「Convergence-guaranteed multiplicative algorithms for nonnegative matrix factorization with β-divergence」（Nakano et al.,2010,IEEE International Workshop）
ISダイバージェンスの妥当性
ISダイバージェンスのみ、複素観測データに対する別の生成モデルが発見されています。
・複素観測データが複素平面で球対称なガウス分布（複素ガウス分布）から生成
・観測データが複数（基底数）個の独立な複素ガウス分布に従う確率変数の線形結合であることを仮定（ガウス分布の再生性）
以上の仮定をすることで、期待値の和として妥当性が保証されています。
乖離度の一般化
上記３種類の乖離度を一般化した関数として、βダイバージェンスが挙げられます。
\begin{eqnarray}
\mathcal{D}_{β}(y|x) &=& \frac{y^{\beta}}{\beta(\beta – 1)} + \frac{x^\beta}{\beta} – \frac{yx^{\beta – 1}}{\beta – 1}\\
\end{eqnarray}
【βダイバージェンスについて】
β$\neq$0, β$\neq$1, であり
・β$\rightarrow$0のとき板倉斎藤擬距離
・β$\rightarrow$1のときIダイバージェンス
・β=2のときユークリッド距離
に対応します。一般に、βが小さければ小さいほど分解のスパース化の制約が大きくなります。
どの乖離度を用いればよいのかという問題は、上でお伝えしたような「生成モデルがどのような事前分布を仮定するか」によると考えられる一方で、「音源分離能力（スパース性）と学習基底挿入能力（アンチスパース性）のトレードオフ」によるという考え方も提案されています。つまり、１つの楽曲の中でも最適な乖離度は変わってくるということなのです。理想的なのは、βを時間変化させられるようなダイバージェンスが利用されるようになることです。
●「On the use of the beta divergence for musical source separation」（ D. FitzGerald/M. Cranitch/E. Coyle,2009,ISSC）
●「Optimal cost function and magnitude power for NMF-based speech separation and music interpolation」（B.King/C.Févotte,P.Smaragdis,2012,IEEE）
●「非負値行列因子分解NMFの基礎とデータ/信号解析への応用」（澤田,2012,電子情報通信学会誌）
●「非負値行列因子分解」（亀岡,2012,NTTコミュニケーション科学基礎研究所 解説：特集 計測・センシングのアルゴリズム）
●「非負値行列因子分解とその音響信号処理への応用」（亀岡,2015,日本統計学会誌）
●音楽音響信号解析のためのスチューデントt分布に基づく非負値行列因子分解と半正定値テンソル分解（吉井/糸山/後藤,2015,電子情報通信学会）
●「Kitamura, Saruwatari et al.,2014,IEEE」
