この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多少意訳した部分もあります。ですので，参考程度におさめていただければ幸いです。間違えている箇所がございましたらご指摘ください。随時更新予定です。
顔のパーツ分解や音源分離，言語処理など様々な場面で応用されるNMF（非負値行列因子分解）ですが，その更新式の導出は意外とごちゃごちゃしています。そこで，この記事ではNMFの更新式の導出を改めて確認していこうと思います。
問題設定
非負値行列因子分解（以下NMF）は、問題設定が大切なので丁寧に見ていきます。NMFでは、ある非負値行列を２つの非負値行列に分解します。
\begin{eqnarray}
\boldsymbol{Y} \simeq \boldsymbol{H}\boldsymbol{U}
\end{eqnarray}
Y：観測値
H：基底行列
U：係数行列
それぞれの行列のサイズは以下の通りとし、要素は実数を取るものとします。
\begin{eqnarray}
\boldsymbol{Y} &\in& \mathbb{R} (K \times N)\\
\boldsymbol{H} &\in& \mathbb{R} (K \times M)\\
\boldsymbol{U} &\in& \mathbb{R} (M \times N)
\end{eqnarray}
これをベクトル表記で書くと、以下のようになります。
\boldsymbol{ y_n } &\simeq& \displaystyle \sum_{ m = 1 }^{ M } \boldsymbol{ h_m }u_{m,n} (n = 1, 2, \ldots, N)\\
\end{eqnarray}
\begin{eqnarray}
\boldsymbol{Y} &=& [\boldsymbol{ y_1 }, \ldots, \boldsymbol{ y_N }] = (y_{k,n})_{K \times N}\\
\boldsymbol{H} &=& [\boldsymbol{ h_1 }, \ldots, \boldsymbol{ h_M }] = (h_{k,m})_{K \times M} \\
\boldsymbol{U} &=& [\boldsymbol{ u_1 }, \ldots, \boldsymbol{ u_N }] = (u_{m,n})_{M \times N}\\
\end{eqnarray}
(5)式の意味は、行列Hと行列Uの乗算を計算するときに、行列Hの列ベクトルと行列Uの各行がかけられていくということを示しています。行列のかけ算の定義です。
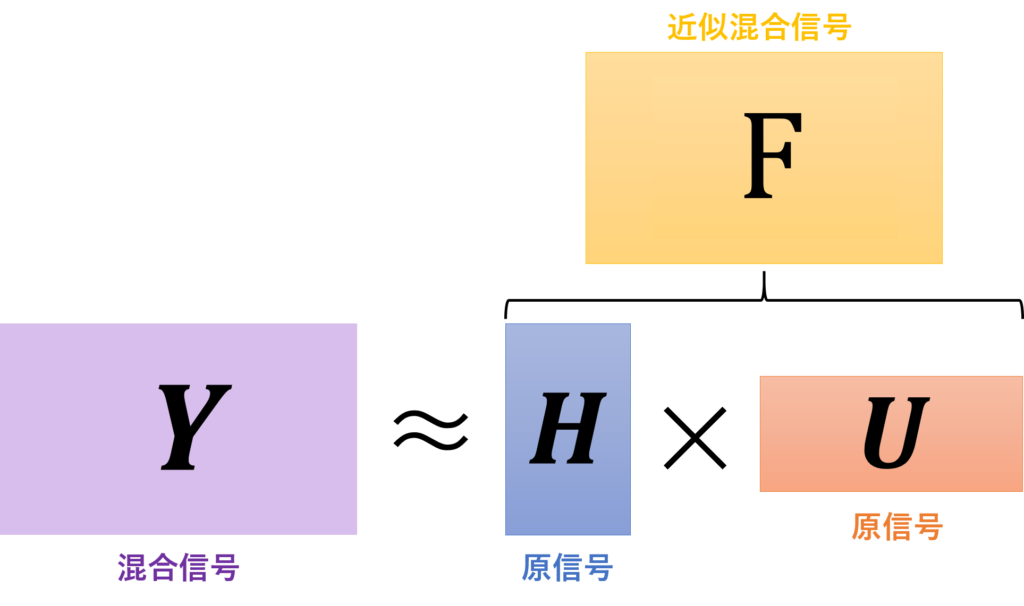NMFの概念図私たちが目指すのは、Yという観測値をHとUのかけ算で近似することです。この近似という言葉が、NMFではカギになります。日本語で説明すると「YとHUがどれだけ数学的に距離が近づくか」という目標です。NMFで「数学的な距離」というのは、一般に以下の距離が利用されます。
「数学的な距離」
●ユークリッド距離（二乗距離）
●Iダイバージェンス
●板倉斎藤擬距離
●βダイバージェンス
●Bregmanダイバージェンス
これらの距離はそれぞれ
\mathcal{D}_{EU}(y|x) &=& (y – x)^2\\
\mathcal{D}_{KL}(y|x) &=& y\log\frac{y}{x} – y + x\\
\mathcal{D}_{IS}(y|x) &=& \frac{y}{x} – \log\frac{y}{x} – 1\\
\mathcal{D}_{β}(y|x) &=& \frac{y^{\beta}}{\beta(\beta – 1)} + \frac{x^\beta}{\beta} – \frac{yx^{\beta – 1}}{\beta – 1}\\
\mathcal{D}_{\varphi}(y|x) &=& \varphi(y) – \varphi (x) – \varphi’ (x)(y – x)\\
\end{eqnarray}
となっています。
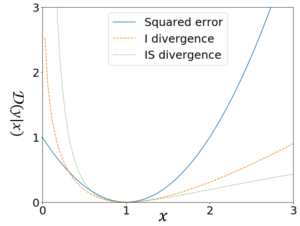各乖離度の比較【βダイバージェンスについて】
β$\neq$0, β$\neq$1, であり
・β$\rightarrow$0のとき板倉斎藤擬距離
・β$\rightarrow$1のときIダイバージェンス
・β=2のときユークリッド距離
に対応します。
【Bregmanダイバージェンスについて】
$\varphi:\mathbb{R} \rightarrow \mathbb{R}$は任意の微分可能関数とします。また
\begin{eqnarray*}
\varphi(z) = \frac{1}{(\beta – 1)\beta}(z^{\beta} – \beta z + \beta – 1)
\end{eqnarray*}
とおけば、βダイバージェンスと等価になります。
またこれらの距離をまとめてHUのYからの距離として，以下のように書くことにします。
\begin{eqnarray}
\mathrm{D}(\boldsymbol{H},\boldsymbol{U})
\end{eqnarray}
以上をまとめると、NMFの問題設定は
$\mathrm{D}(\boldsymbol{H},\boldsymbol{U})$を最小化する$\boldsymbol{H}$と$\boldsymbol{U}$を見つける（※）
ということになります。
補助関数法
（※）の最適化問題は、解析的に解くことができません。
そこで利用されるのが「補助関数法」という考え方です。NMFにおける補助関数法はLeeらによって考案された手法で、目的関数の上限関数を作り上限を反復的に最小化していくことで、目的関数を間接的に最小化するというアイディアです。定義と定理を以下に示します。
【定義】
$θ = {θ_i}_{(i=1,\ldots,I)}$を変量とする目的関数$\mathrm{D}(θ)$に対し、新しい変量$\bar{θ}$を導入して以下が成り立つとき
\begin{eqnarray}
\mathrm{D}(θ) = \min_{\bar{θ}} \mathrm{G}(θ,\bar{θ})
\end{eqnarray}
$\mathrm{G}(θ,\bar{θ})$を$\mathrm{D}(θ)$の補助関数、$\bar{θ}$を補助変数と定義する。
【定理】
補助関数$\mathrm{G}(θ,\bar{θ})$を、$\bar{θ}$に関して最小化するステップと、θに関して最小化するステップを繰り返すと、目的関数$\mathrm{D}(θ)$は単調減少する。
\begin{eqnarray}
&&\bar{θ} ← \mathrm{arg}\min_{\bar{θ}} \mathrm{G}(θ,\bar{θ})\\
&&θ ← \mathrm{arg}\min_{θ} \mathrm{G}(θ,\bar{θ})
\end{eqnarray}
以下は定理の証明です。まずは式（16）と式（17）を反復回数を表すkを用いて更に詳しく書き直します。
&&\bar{\theta}^{(k+1)} ← \mathrm{arg}\min_{\bar{\theta}} \mathrm{G}(\theta^{(k)},\bar{\theta})\\
&&\theta^{(k+1)} ← \mathrm{arg}\min_{\theta} \mathrm{G}(\theta,\bar{\theta}^{(k+1)})
\end{eqnarray}
式（18）は式（15）の定義より
\begin{eqnarray}
\mathrm{G}(\theta^{(k)},\bar{\theta}^{(k+1)}) = \mathrm{D}(\theta^{(k)})
\end{eqnarray}
となります。次に式（19）より$\theta^{(k+1)}$は$\mathrm{G}(\theta^{(k)},\bar{\theta}^{(k+1)})$を最小化するので、任意の$\theta$に対して
\begin{eqnarray}
\mathrm{G}(\theta^{(k+1)},\bar{\theta}^{(k+1)}) \leqq \mathrm{D}(\theta,\bar{\theta}^{(k+1)})
\end{eqnarray}
が成り立ちます。任意の$\theta$に対して成り立つので$\theta＝\theta^{(k)}$を代入すれば
\mathrm{G}(\theta^{(k+1)},\bar{\theta}^{(k+1)}) \leqq \mathrm{G}(\theta^{(k)},\bar{\theta}^{(k+1)})
\end{eqnarray}
となります。ここで再び定義式（15）より任意のθに対して
\begin{eqnarray}
\mathrm{D}(\theta) \leqq \mathrm{G}(\theta,\bar{\theta}^{(k+1)})
\end{eqnarray}
ですから、$\theta＝\theta^{(k)}$を代入すれば
\begin{eqnarray}
\mathrm{D}(\theta^{(k+1)}) \leqq \mathrm{G}(\theta^{(k+1)},\bar{\theta}^{(k+1)})
\end{eqnarray}
が成り立ちます。以上(20)(22)(24)式から
\begin{eqnarray}
\mathrm{D}(\theta^{(k+1)}) \leqq \mathrm{D}(\theta^{(k)})
\end{eqnarray}
となり、更新ステップを繰り返すことで目的関数が単調減少することが示されました。
更新式の導出
ユークリッド距離（二乗距離）
最小化する目的関数は
\begin{eqnarray}
\mathcal{D}_{EU}(\boldsymbol{Y} | \boldsymbol{HU})
\end{eqnarray}
です。実際に展開して、$\boldsymbol{HU}$に関係ある項だけ残したものを改めて$\mathcal{D}_{EU}(\boldsymbol{Y} | \boldsymbol{HU})$と置きます。
\mathcal{D}_{EU}(\boldsymbol{Y} | \boldsymbol{HU})
&=& (\boldsymbol{Y} – \boldsymbol{HU})^2\\
&=& \sum_{ k,n }^{} ( y_{k,n}^2 – 2y_{k,n}\sum_{ m }^{} h_{k,m}u_{m,n} + (\sum_{ m }^{} h_{k,m}u_{m,n})^2 )\\
&\overset{h,u}{=}& \sum_{ k,n }^{} ( – 2y_{k,n}\sum_{ m }^{} h_{k,m}u_{m,n} + (\sum_{ m }^{} h_{k,m}u_{m,n})^2 )
\end{eqnarray}
この式を微分して０になる$h_{k,m}$と$u_{m,n}$を求めればよいのですが、第２項目が合成関数の形になっており、微分してもシグマが残ってしまうため解析的に解くことができません。そこで、先ほど述べた補助関数法を用いて反復的に近似解を求めるアプローチをとりたいと思います。補助関数法を用いるために、まずは上限関数を設定しましょう。NMFで上限関数を作るためによく使われるのが以下の「Jensenの不等式」です。
「Jensenの不等式」
任意の凸関数g，I個の実数$x_1, \ldots, x_I$，$\sum_{i}^{} \lambda_i = 1$を満たす正の重み関数$\lambda_1, \ldots, \lambda_I$の下で、以下の不等式が成り立つ。
\begin{eqnarray}
g(\sum_{ i }^{} \lambda_i z_i) \leq \sum_{i}^{}\lambda_i g(z_i)
\end{eqnarray}
(ただし、等号成立は$z_1 = z_2 = \ldots, =z_I$のとき)
さて、$\lambda_{k,m,n} \gt 0$、$\sum_{ m }^{} \lambda_{k,m,n}=1$なる補助変数$\lambda_{k,m,n}$を導入して、「Jensenの不等式」を式（29）に適用します。
\mathcal{D}_{EU}(\boldsymbol{Y} | \boldsymbol{HU})
&=& \sum_{ k,n }^{} ( – 2y_{k,n}\sum_{ m }^{} h_{k,m}u_{m,n} + (\sum_{ m }^{} \lambda_{k,m,n} \frac{h_{k,m}u_{m,n}}{\lambda_{k,m,n}})^2)\\
&\leq& \sum_{ k,n }^{} ( – 2y_{k,n}\sum_{ m }^{} h_{k,m}u_{m,n} + \sum_{ m }^{} \lambda_{k,m,n} (\frac{h_{k,m}u_{m,n}}{\lambda_{k,m,n}})^2)\\
&=& \sum_{ k,n }^{} ( – 2y_{k,n}\sum_{ m }^{} h_{k,m}u_{m,n} + \sum_{ m }^{} \frac{h_{k,m}^2 u_{m,n}^2}
{\lambda_{k,m,n}} )
\end{eqnarray}
このとき、等号は
\begin{eqnarray}
\lambda_{k,m,n} = \frac{h_{k,m}u_{m,n}}{\sum_{ m }^{} h_{k,m}u_{m,n}}
\end{eqnarray}
のときに成立します。実はこの式（34）が$\lambda$の更新式そのものになります。さて、ここまでの流れをまとめてみます。$\lambda$の行列表現を$\boldsymbol{\lambda}(K \times M \times N)$、上限関数を$\mathrm{G}_{EU}(\boldsymbol{H},\boldsymbol{U},\boldsymbol{\lambda})$と書くことにすると
\begin{eqnarray}
\mathcal{D}_{EU}(\boldsymbol{Y} | \boldsymbol{HU})
\leq \mathrm{G}_{EU}(\boldsymbol{H},\boldsymbol{U},\boldsymbol{\lambda})
\end{eqnarray}
であり、式（34）より$\boldsymbol{\lambda}$は補助変数の要件を満たすので、式（35）より$\mathrm{G}_{EU}(\boldsymbol{H},\boldsymbol{U},\boldsymbol{\lambda})$は$\mathcal{D}_{EU}(\boldsymbol{Y} | \boldsymbol{HU})
$の上限関数となります。
あとは$h_{k,m}$と$u_{m,n}$について上限関数を偏微分して上限関数を最小にする$h_{k,m}$と$u_{m,n}$を見つけるだけです。偏微分も見かけ倒しで、そこまで複雑な計算ではないのでビビる必要はありません。シグマが付いている項だけ微分の際に注意しましょう。実際に計算してみます。
\frac{ \partial \mathrm{G} }{ \partial h_{k,m} }
&=& \sum_{ n }^{} ( – 2y_{k,n}u_{m,n} + 2\frac{h_{k,m}u_{m,n}^2}{\lambda_{k,m,n}}) = 0\\
\frac{ \partial \mathrm{G} }{ \partial u_{m,n} }
&=& \sum_{ k }^{} ( – 2y_{k,n}h_{k,m} + 2\frac{h_{k,m}^2u_{m,n}}{\lambda_{k,m,n}}) = 0
\end{eqnarray}
\begin{eqnarray}
h_{k,m} &=& \frac{\sum_{n}^{} y_{k,n}u_{m,n}}{\sum_{n}^{} \frac{u_{m,n}^2}{\lambda_{k,m,n}}}\\
u_{m,n} &=& \frac{\sum_{k}^{} y_{k,n}h_{k,m}}{\sum_{k}^{} \frac{h_{k,m}^2}{\lambda_{k,m,n}}}
\end{eqnarray}
補助変数を代入しましょう。
h_{k,m} &=& h_{k,m} \frac{\sum_{n}^{} y_{k,n}u_{m,n}}{\sum_{n}^{} u_{m,n} \sum_{m}^{} h_{k,m}u_{m,n}}\\
u_{m,n} &=& u_{m,n} \frac{\sum_{k}^{} y_{k,n}h_{k,m}}{\sum_{k}^{} h_{k,m} \sum_{m}^{} h_{k,m}u_{m,n}}
\end{eqnarray}
見事更新式が導出できました。これで終わりとしても良いのですが、実は式（40）と式（41）は行列表記にすると非常にスッキリします。実装のプログラミングでも行列表記にしておくと見通しが良くなるので、実際に変形してみましょう。
\begin{eqnarray}
h_{k,m} &=& h_{k,m} \frac{[\boldsymbol{Y}\boldsymbol{U^{\mathrm{T}}}]_{k,m}}{[\boldsymbol{HU}\boldsymbol{U^{\mathrm{T}}}]_{k,m}}\\
u_{m,n} &=& u_{m,n} \frac{[\boldsymbol{H^{\mathrm{T}}}\boldsymbol{Y}]_{m,n}}{[\boldsymbol{H^{\mathrm{T}}}\boldsymbol{HU}]_{m,n}}
\end{eqnarray}
となります。シグマが厄介そうに見えて、意外とシンプルな計算で済むのがNMFの更新式の特徴です。
Iダイバージェンス
流れはユークリッド距離基準と変わりません。最小化する目的関数は
\begin{eqnarray}
\mathcal{D}_{I}(\boldsymbol{Y} | \boldsymbol{HU})
\end{eqnarray}
です。実際に展開して、$\boldsymbol{HU}$に関係ある項だけ残したものを改めて$\mathcal{D}_{I}(\boldsymbol{Y} | \boldsymbol{HU})$と置きます。
\mathcal{D}_{I}(\boldsymbol{Y} | \boldsymbol{HU})
&=& \boldsymbol{Y} \log \frac{\boldsymbol{Y}}{\boldsymbol{HU}} – \boldsymbol{Y} + \boldsymbol{HU} \\
&=& \sum_{ k,n } ( y_{k,n} \log \frac{y_{k,n}}{\sum_{m} h_{k,m}u_{m,n}} – y_{k,n} + \sum_{ m } h_{k,m}u_{m,n})\\
&=& \sum_{ k,n } ( y_{k,n} \log y_{k,n} – y_{k,n} \log \sum_{m} h_{k,m}u_{m,n} – y_{k,n} + \sum_{ m } h_{k,m}u_{m,n})\\
&\overset{h,u}{=}& \sum_{ k,n } ( – y_{k,n} \log \sum_{m} h_{k,m}u_{m,n} + \sum_{ m } h_{k,m}u_{m,n})
\end{eqnarray}
ここで、第一項目に注目すると「log-sum」の形になっており、微分しても解析的に解くことができません。第一項目は「$- \log x$」関数で凸関数なので「Jensenの不等式」が適用できます。そこで、ユークリッド距離同様に「Jensenの不等式」を利用して上限関数を設定しましょう。
$\lambda_{k,m,n} \gt 0$、$\sum_{ m }^{} \lambda_{k,m,n}$なる補助変数$\lambda_{k,m,n}$を導入して、「Jensenの不等式」を式（48）に適用します。
\mathcal{D}_{I}(\boldsymbol{Y} | \boldsymbol{HU})
&=& \sum_{ k,n } ( – y_{k,n} \log \sum_{m} h_{k,m}u_{m,n} + \sum_{ m } h_{k,m}u_{m,n})\\
&=& \sum_{ k,n } ( – y_{k,n} \log \sum_{m} \lambda_{k,m,n} \frac{h_{k,m}u_{m,n}}{\lambda_{k,m,n}} + \sum_{ m } h_{k,m}u_{m,n})\\
&\leq& \sum_{ k,n } ( – y_{k,n} \sum_{m} \lambda_{k,m,n} \log \frac{h_{k,m}u_{m,n}}{\lambda_{k,m,n}} + \sum_{ m } h_{k,m}u_{m,n})\\
&\equiv& \mathrm{G}_{I}(\boldsymbol{H},\boldsymbol{U},\boldsymbol{\lambda})
\end{eqnarray}
このとき、等号は
\begin{eqnarray}
\lambda_{k,m,n} = \frac{h_{k,m}u_{m,n}}{\sum_{ m }^{} h_{k,m}u_{m,n}}
\end{eqnarray}
のときに成立します。あとは補助関数$\mathrm{G}_{I}(\boldsymbol{H},\boldsymbol{U},\boldsymbol{\lambda})$を微分して0になる$h_{k,m}$と$u_{m,n}$を計算すれば良いだけです。実際に計算してみましょう。
\frac{ \partial \mathrm{G} }{ \partial h_{k,m} }
&=& \sum_{n} (- y_{k,n} \lambda_{k,m,n} \frac{\lambda_{k,m,n}}{h_{k,m}u_{m,n}} \frac{u_{m,n}}{\lambda_{k,m,n}} + u_{m,n})\\
&=& – \frac{1}{h_{k,m}} \sum_{n} y_{k,n} \lambda_{k,m,n} + \sum_{n} u_{m,n} = 0\\
\frac{ \partial \mathrm{G} }{ \partial u_{m,n} }
&=& \sum_{k} (- y_{k,n} \lambda_{k,m,n} \frac{\lambda_{k,m,n}}{h_{k,m}u_{m,n}} \frac{h_{k,m}}{\lambda_{k,m,n}} + h_{k,m})\\
&=& – \frac{1}{u_{m,n}} \sum_{k} y_{k,n} \lambda_{k,m,n} + \sum_{k} h_{k,m} = 0
\end{eqnarray}
\begin{eqnarray}
h_{k,m} = \frac{\sum_{n} y_{k,n} \lambda_{k,m,n}}{\sum_{n} u_{m,n}}\\
u_{m,n} = \frac{\sum_{k} y_{k,n} \lambda_{k,m,n}}{\sum_{k} h_{k,m}}
\end{eqnarray}
補助変数を代入しましょう。
\begin{eqnarray}
h_{k,m} = h_{k,m} \frac{\sum_{n} \frac{y_{k,n} u_{m,n}}{\sum_{m} h_{k,m} u_{m,n}}}{\sum_{n} u_{m,n}}\\
u_{m,n} = u_{m,n} \frac{\sum_{k} \frac{y_{k,n} h_{k,m}}{\sum_{m} h_{k,m} u_{m,n}}}{\sum_{k} h_{k,m}}
\end{eqnarray}
見事更新式が導出できました。
板倉斎藤擬距離
流れはユークリッド距離基準と変わりません。最小化する目的関数は
\begin{eqnarray}
\mathcal{D}_{IS}(\boldsymbol{Y} | \boldsymbol{HU})
\end{eqnarray}
です。
実際に展開して、$\boldsymbol{HU}$に関係ある項だけ残したものを改めて$\mathcal{D}_{IS}(\boldsymbol{Y} | \boldsymbol{HU})$と置きます。
\mathcal{D}_{IS}(\boldsymbol{Y} | \boldsymbol{HU})
&=& \sum_{ k,n } ( \frac{\boldsymbol{Y}}{\boldsymbol{HU}} – \log \frac{\boldsymbol{Y}}{\boldsymbol{HU}} – 1 )\\
&=& \sum_{ k,n } ( \frac{y_{k,n}}{x_{k,n}} – \log \frac{y_{k,n}}{x_{k,n}} – 1 )\\
&\overset{h,u}{=}& \sum_{ k,n } ( \frac{y_{k,n}}{x_{k,n}} + \log x_{k,n} )
\end{eqnarray}
ただし、$\sum_{m} h_{k,m}u_{m,n} = x_{k,n}$と置きました。
以下同様に、補助関数を作っていきます。…としたいところですが、第二項目に「$+ \log x$関数」という凹関数が出てきてしまっています。凹関数には「Jensenの不等式」が適用できないので、代わりに接線不等式を利用して、目的関数を上からおさえることで補助関数を作ります。
【接線不等式】
任意の微分可能な凹関数に関して
\begin{eqnarray}
g(x) \leq g(\alpha) + g'(\alpha)(x – \alpha)
\end{eqnarray}
ただし、等号成立は$x = \alpha$
まず、第一項目に関して「Jensenの不等式」を利用して
\begin{eqnarray}
\frac{1}{x_{k,n}} &=& \frac{1}{\sum_{m}h_{k,m}u_{m,n}}\\
&=& \frac{1}{\sum_{m} \lambda_{k,m,n} \frac{h_{k,m}u_{m,n}}{\lambda_{k,m,n}}}\\
&\leq& \sum_{m} \lambda_{k,m,n} \frac{1}{ \frac{h_{m,n}u_{m,n}}{\lambda_{k,m,n}}}\\
&=& \sum_{m} \frac{\lambda_{k,m,n}^2}{h_{k,m}u_{m,n}}
\end{eqnarray}
ただし、等号は
\begin{eqnarray}
\lambda_{k,m,n} = \frac{h_{k,m}u_{m,n}}{\sum_{m}h_{k,m}u_{m,n}}
\end{eqnarray}
のときに成立します。次に、第二項目に関して「接線不等式」を利用して
\log \sum_{m} h_{k,m}u_{m,n}
&\leq& \frac{1}{c_{k,n}}(\sum_{m}h_{k,m}u_{m,n} – c_{k,n}) + \log c_{k,n}\\
&\overset{h,u}{=}& \frac{\sum_{m}h_{k,m}u_{m,n}}{c_{k,n}}
\end{eqnarray}
ただし、等号は
\begin{eqnarray}
c_{k,n} = \sum_{m}h_{k,m}u_{m,n}
\end{eqnarray}
のときに成立します。式（65）に式（70）と式（72）を適用すると
\mathcal{D}_{IS}(\boldsymbol{Y} | \boldsymbol{HU})
&\leq& \sum_{k,n}( \sum_{m} \frac{\lambda_{k,m,n}^2 y_{k,n}}{h_{k,m}u_{m,n}} + \frac{\sum_{m}h_{k,m}u_{m,n}}{c_{k,n}})\\
&\equiv& \mathrm{G}_{IS}(\boldsymbol{H},\boldsymbol{U},\boldsymbol{\lambda})
\end{eqnarray}
となります。あとは、今までの議論と全く同じ流れです。パラメータの数が２つに増えているものの、本質的な操作は変わりありません。
式（67）から式（74）を参照すれば、$\mathrm{G}_{IS}(\boldsymbol{H},\boldsymbol{U},\boldsymbol{\lambda})$が補助関数の要件を満たしていることが分かります。それでは、補助関数を偏微分して更新式を導出していきましょう。
\frac{ \partial \mathrm{G} }{ \partial h_{k,m} }
&=& \sum_{n} (\frac{\lambda_{k,m,n}^2 y_{k,n}}{u_{m,n}}(- \frac{1}{h_{k,m}^2}) + \frac{u_{m,n}}{c_{k,n}}) = 0\\
\frac{ \partial \mathrm{G} }{ \partial u_{m,n} }
&=& \sum_{k} (\frac{\lambda_{k,m,n}^2 y_{k,n}}{h_{k,m}}(- \frac{1}{u_{m,n}^2}) + \frac{h_{k,m}}{c_{k,n}}) = 0
\end{eqnarray}
$h_{k,m}^2$と$u_{m,n}^2$を移行して整理していきましょう。
h_{k,m}^2 &=& \frac{\sum_{n} \frac{\lambda_{k,m,n}^2 y_{k,n}}{u_{m,n}}}{\sum_{n} \frac{u_{m,n}}{c_{k,n}}}
&=& h_{k,m}^2 \frac{\sum_{n} \frac{u_{m,n}y_{k,n}}{x_{m,n}^2}}{\sum_{n} \frac{u_{m,n}}{x_{k,n}}}\\
u_{m,n}^2 &=& \frac{\sum_{k} \frac{\lambda_{k,m,n}^2 y_{k,n}}{h_{k,m}}}{\sum_{k} \frac{h_{k,m}}{c_{k,n}}}
&=& u_{m,n}^2 \frac{\sum_{k} \frac{h_{k,m}y_{k,n}}{x_{m,n}^2}}{\sum_{k} \frac{h_{k,m}}{x_{k,n}}}
\end{eqnarray}
非負値の制限がありますから、両辺のルートを取れば更新式が手に入ります。
\begin{eqnarray}
h_{k,m} &=& h_{k,m} (\frac{\sum_{n} \frac{u_{m,n}y_{k,n}}{x_{m,n}^2}}{\sum_{n} \frac{u_{m,n}}{x_{k,n}}})^{\frac{1}{2}}\\
u_{m,n} &=& u_{m,n} (\frac{\sum_{k} \frac{h_{k,m}y_{k,n}}{x_{m,n}^2}}{\sum_{k} \frac{h_{k,m}}{x_{k,n}}})^{\frac{1}{2}}
\end{eqnarray}
見事、更新式を導出できました。
βダイバージェンス
以上の３種類の乖離度を一般化したものが、βダイバージェンスです。βダーバージェンスは、βの大きさによって目的関数が凸関数か凹関数かが変わってしまうので、場合分けして求めることになります。
詳しくは以下の論文をご覧ください。もしご要望がありましたら、こちらのサイトで詳しく導出フォローさせていただきます。
●「Convergence-guaranteed multiplicative algorithms for nonnegative matrix factorization with β-divergence」（Nakano/kameoka/…,2010,IEEE International Workshop on Machine Learning for Signal Processing）
Bregmanダイバージェンス
βダイバージェンスをさらに一般化したものが、Bregmanダイバージェンスです。こちらは、一般化された微分可能で凸な関数$\varphi$に対する更新式はまだ発見されておりません。
詳しくは以下の論文をご覧ください。もしご要望がありましたら、こちらのサイトで詳しく導出フォローさせていただきます。
●「Generalized nonnegative matrix approximations with Bregman divergences」（Dhillon, 2005, NIPS）
注意事項
NMFのアルゴリズムは、乗法的な更新式です。これは、実数の減算によって係数を更新する最急降下法とは対照的です。なぜNMFで乗法的な更新式が用いられているかというのは、以下の理由によります。
・「非負値」の情報が引き継がれる
・「０」の情報が反映されやすくスパース化につながる
●「非負値行列因子分解」（亀岡,2012,NTTコミュニケーション科学基礎研究所 解説：特集 計測・センシングのアルゴリズム）
●「補助関数法による最適化アルゴリズムとその音響信号処理への応用」（小野,2012,日本音響学会誌）
●「統計的音響信号処理の新展開」（吉井/糸山、2015,映像情報メディア学会誌）
●「非負値行列因子分解NMFの基礎とデータ/信号解析への応用」（澤田,2012,電子情報通信学会誌）
●「スパース表現と凸最適化に基づく非負値行列因子分解と音楽信号処理への応用」（湯川,2017,TELECOM FRONTIER）
訂正をお願いします。
式番号(8)hm,n → um,n
(37) Σm → Σk
ご指摘誠にありがとうございます。
修正致しました。
すみません、式60, 61に関して、行列表記への変換がよくわかりません。
多分、シグマの使い方が良く分かっていないのだと思います。
割り算は、行列の割り算を示しているのでしょうか？
bsc様
ご質問ありがとうございます。
行列表記への変形ですが，二乗距離の場合と同様に考えればOKです。
つまり，行列の積を計算できるように適宜転置を行いながら，対応するインデックスを抽出するということです。
また，割り算は，スカラーの割り算を表しています。
$h$の$(k,m)$要素を更新するためには，$\sum_{n} \frac{y_{k,n} u_{m,n}}{\sum_{m} h_{k,m} u_{m,n}}$というスカラーを$\sum_{n} u_{m,n}$というスカラーで割って元の値に掛け合わせれば良いということです。