今回は,scikit-learnなどの既成ライブラリにできるだけ頼らずに,フィッシャーの線形判別分析法の基本的な部分を実装していこうと思います。また,本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。
必要なモジュールのインポート
import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt
cm = plt.get_cmap("tab10")数値計算のためのnumpy,(行列計算のためのlinalg),グラフ出力のためのpyplot,配色をするためのc_mapをインポートします。
データの生成
m1 = np.array([10, 5])
s1 = np.array([[1, 2], [2, 5]])
m2 = np.array([1, 3])
s2 = np.array([[1, 2], [2, 5]])
N = 100
x1 = np.random.multivariate_normal(m1, s1, N)
x2 = np.random.multivariate_normal(m2, s2, N)
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.show()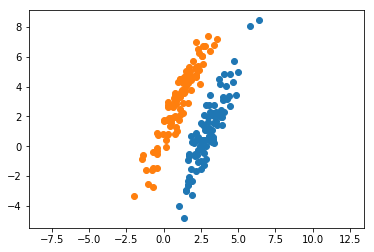 numpyのmultivariate_normalを利用して,適当な平均と共分散行列からデータを生成しておきます。以下では,これらのデータとクラスが「与えられたもの」としてフィッシャーの線形判別分析を施していきます。以下の記事で,主成分分析との違いを考察しています。
numpyのmultivariate_normalを利用して,適当な平均と共分散行列からデータを生成しておきます。以下では,これらのデータとクラスが「与えられたもの」としてフィッシャーの線形判別分析を施していきます。以下の記事で,主成分分析との違いを考察しています。

クラス内共分散行列を求める関数
\begin{eqnarray}
&\boldsymbol{w}& \propto \boldsymbol{S}_w^{-1}(\boldsymbol{m}_2 – \boldsymbol{m}_1) \\
&\boldsymbol{S}_w^{-1}& = \sum_{n\in C_1}{(\boldsymbol{x}_n – \boldsymbol{m}_1)(\boldsymbol{x}_n – \boldsymbol{m}_1)}^T + \sum_{n\in C_2}{(\boldsymbol{x}_n – \boldsymbol{m}_2)(\boldsymbol{x}_n – \boldsymbol{m}_2)}^T
\end{eqnarray}
def cal_sw(x1, m1, x2, m2):
sw = ((x1 - m1).T @ (x1 - m1)) + ((x2 - m2).T @ (x2 - m2))
return swフィッシャーの線形判別分析による重みパラメータは,式(1)のようにして求められます。式(1)を求めるために,まずはクラス内共分散行列である式(2)を求める関数を作っています。
実際に計算
w = LA.inv(cal_sw(x1, m1, x2, m2)) @ (m2 - m1)式(1)に従って,重みパラメータを計算しています。
グラフ出力の準備
xlist = np.arange(-5,10,0.1)
ylist = m[1] + (w[1]/w[0]) * (xlist - m[0])
ydisc = m[1] + (-w[0]/w[1]) * (xlist - m[0])x軸は適当にとっています。ylistはフィッシャーの基準に従って求めた射影先の軸,ydiscはその軸に直交するような識別面を表しています。
グラフ出力
plt.plot(xlist, ylist, color=cm(4))
plt.plot(xlist, ydisc, linestyle='dashed', color='black')
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.ylim(-6,12)
plt.show()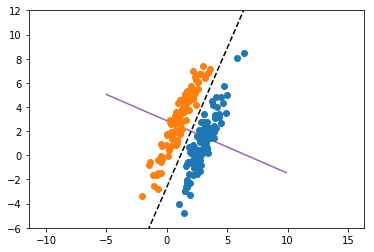
実線がFisherの基準による射影先の軸,点線がそれに直交する識別面を表しています。
考察
フィッシャーの線形判別分析は,名前の通りクラス判別のために使用される手法です。実際に,出力されたグラフの点線で2つのクラスがきれいに判別できることが分かります。フィッシャーの判別基準では,クラス内の分散が小さく,かつクラス間の分散が大きくなるように線形な識別面を設定しました。
これは,単純に「射影先でクラスの平均値がよく離れている」という基準で設定した識別面よりも良い結果を与えます。なぜなら,平均だけで分離の良さを比較しようとすると,データの広がり(分散)を無視することになるからです。データの広がり(分散)を使って分離の良さを記述したものが,フィッシャーの判別基準になります。
\begin{eqnarray}
J(\boldsymbol{w}) = \frac{\mbox{クラス間分散}}{\mbox{クラス内分散}}
\end{eqnarray}
もし理論にモヤモヤがあれば
(2026/02/12 16:31:04時点 楽天市場調べ-詳細)
こちらの参考書は,PRMLよりも平易に機械学習全般の手法について解説しています。おすすめの1冊になりますので,ぜひお手に取って確認してみてください。
全コード
import numpy as np
import matplotlib.pyplot as plt
cm = plt.get_cmap("tab10")
m1 = np.array([3, 1])
s1 = np.array([[1, 2], [2, 5]])
m2 = np.array([1, 3])
s2 = np.array([[1, 2], [2, 5]])
N = 100
x1 = np.random.multivariate_normal(m1, s1, N)
x2 = np.random.multivariate_normal(m2, s2, N)
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.show()
m1 = np.array([3, 1])
s1 = np.array([[1, 2], [2, 5]])
m2 = np.array([1, 3])
s2 = np.array([[1, 2], [2, 5]])
N = 100
x1 = np.random.multivariate_normal(m1, s1, N)
x2 = np.random.multivariate_normal(m2, s2, N)
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.show()
def cal_sw(x1, m1, x2, m2):
sw = ((x1 - m1).T @ (x1 - m1)) + ((x2 - m2).T @ (x2 - m2))
return sw
w = LA.inv(cal_sw(x1, m1, x2, m2)) @ (m2 - m1)
xlist = np.arange(-5,10,0.1)
ylist = m[1] + (w[1]/w[0]) * (xlist - m[0])
ydisc = m[1] + (-w[0]/w[1]) * (xlist - m[0])
plt.plot(xlist, ylist, color=cm(4))
plt.plot(xlist, ydisc, linestyle='dashed', color='black')
plt.plot(x1[:,0], x1[:,1], 'o', color=cm(0))
plt.plot(x2[:,0], x2[:,1], 'o', color=cm(1))
plt.axis('equal')
plt.ylim(-6,12)
plt.show()

















zukaさん
判別分析を、既存の関数に頼らずPythonで書こうとしておりました。
なので、大変助かりました!
zukaさんのコードを実行するとエラーになりした。
ylist = m[1] + (w[1]/w[0]) * (xlist – m[0])
ydisc = m[1] + (-w[0]/w[1]) * (xlist – m[0])
のところで、mが定義されていないためかと思われます。
今後とも、よろしくお願い致します!
リトルトゥース様
ご指摘誠にありがとうございます!
現在やや取り込んでおり,時間を見つけて修正するようにします。
これからもよろしくお願い致します。