【超丁寧に】RSAに利用されている数式を数学ド素人に向けて分かりやすく解説します!

本記事は教養記事シリーズその29です。その他の教養記事はコチラの目次をご覧ください。
RSAとは?
どのような仕組み?
使われている数学理論は?
何がポイント?
RSAとは
RSAとは公開鍵暗号化方式を実現するための手法の1つです。RSAという名前は,開発メンバーであるリベスト氏,シャミア氏,エーデルマン氏の頭文字に由来しています。公開鍵暗号化方式に関しては,コチラの記事で丁寧に解説しています。RSA以外にも,暗号化方式ではいろいろな手法(アルゴリズム)が用いられてきました。
【共通鍵暗号化方式の手法】
●DES:安全性が低い
●トリプルDES:ある程度安全だが計算量が多い
●AES:最も広く利用されている
【公開鍵暗号化方式の手法】
●DH:ある程度安全だが計算量が多い
●ECC:処理速度早いが安全性と利便性△
●RSA:最も広く利用されている
RSAの流れ
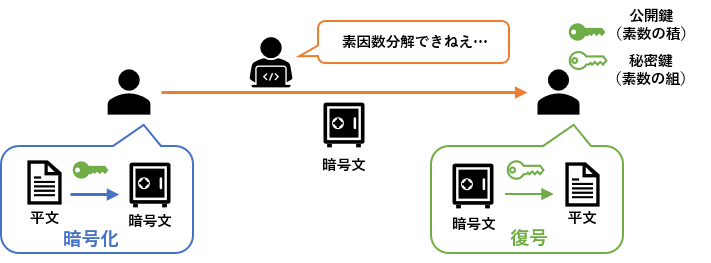 RSAの流れ
RSAの流れRSAの詳しい解説に入る前に,全体の流れを説明しておこうと思います。RSAでは「大きな数の素因数分解がとても難しい」という性質を利用して暗号化を行います。コチラの記事で例えているように,レシピ通りにカレーを作ることは簡単でも,出されたカレーから具材の種類と量を完璧に言い当てることは難しいです。それと同じで,大きな数を素因数分解するのは非常に難しいのです。
 カレーの具材を正確に言い当てられない
カレーの具材を正確に言い当てられないそして,素因数分解することで得られる情報は数学の定理に応用されます。「オイラーの定理」と呼ばれる有名な定理を利用することで,RSA暗号化のしくみは成り立っています。
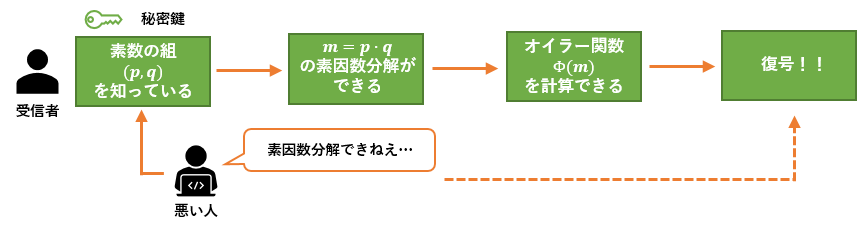 得られた情報は数学の定理を利用します
得られた情報は数学の定理を利用します利用する数学の定理
さて,ここから数式を利用していきます。身構える必要はありません!一緒に少しずつ着実に理解していけば大丈夫です。RSAでは,主に「オイラーの定理(→フェルマーの小定理)」「ユークリッドの互除法」「一次不定方程式の整数解の存在定理」が用いられます。順番に確認していきましょう。
【オイラーの定理】
正の整数$a$,$m$に対して,$a$, $m$が互いに素であるとき,以下が成り立つ。
\begin{eqnarray}
a^{\varphi(m)}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
ただし,$\varphi(m)$は「$m$より小さい正の整数のうち,$m$と互いに素な数の個数」を表すオイラー関数とする。
【フェルマーの小定理】
オイラーの定理において,正の整数$m$が素数$p$であるとき,以下が成り立つ。
\begin{eqnarray}
a^{(p-1)}\equiv1\ ({\rm mod}\ p)
\end{eqnarray}
【ユークリッドの互除法】
自然数$a$,$b(a≥b)$に対して,$a$を$b$で割った余りを$r$とおくとき,以下が成り立つ。
\begin{eqnarray}
gcd(a, b)=gcd(b, r)
\end{eqnarray}
ただし,$gcd(a, b)$は$a$と$b$の最大公約数を表す。
【一次不定方程式の整数解の存在定理】
$a$,$b$を互いに素な整数としたとき,以下の方程式を満たすような整数解$u$,$v$が存在する。
\begin{eqnarray}
au+bv=1
\end{eqnarray}
これらの定理を利用して,RSAのしくみを探っていきたいと思います。
数学的な説明
ここからは,文字を利用して数学的な解説をしていこうと思います。数学が苦手な方も,1行ずつ追いつくようにすれば必ず理解できると思いますので,一緒に頑張っていきましょう。
まずは,文字を決めます。
$A$:平文
$B$:暗号文
$p$:大きな素数
$q$:大きな素数
$l_a$:復号のための定数$(>0)$
$l_b$:暗号化のための定数
$m$:公開鍵の要素
$k$:公開鍵
$s$:秘密鍵
ただし,以下のように定めます。
$m=p \cdot q$
$k=\{l_b, m\}$
$s=l_a$
このとき,平文と暗号文は以下のように表されます。
\begin{eqnarray}
B \equiv A^{l_b}\ ({\rm mod}\ m)\\
A \equiv B^{l_a}\ ({\rm mod}\ m)
\end{eqnarray}
その通りです。少し,今の状況を整理します。
$A$:平文→知っている
$B$:暗号文→方法は知っている
$p$:大きな素数→適当に作る
$q$:大きな素数→適当に作る
$l_b$:暗号化のための定数→知らない
$l_a$:復号のための定数→知らない
$m$:公開鍵の要素→知っている
$k$:公開鍵→片方知らない
$s$:秘密鍵→知らない
ただし,以下のように定めます。
$m=p \cdot q$
$k=\{l_b, m\}$
$s=l_a$
というような具合です。そこで,以下では「知らない」となっている要素に関して,数学の定理を利用しながら求めていきたいと思います。まずは,式(5)に式(6)を代入します。そうすると,このようになります。
\begin{eqnarray}
B \equiv B^{l_{a}l_{b}}\ ({\rm mod}\ m)
\end{eqnarray}
今後,この式(7)が成立することを証明すれば,暗号化と復号が上手くいっている証明になります。そこで,式変形を進めていきたいと思います。両辺を$B$で割ると
\begin{eqnarray}
B^{l_{a}l_{b} – 1}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
その通りです。オイラーの定理と少し並べてみてみましょう。
【オイラーの定理】
\begin{eqnarray}
a^{\varphi(m)}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
【今回の式】
\begin{eqnarray}
B^{l_{a}l_{b} – 1}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
オイラーの定理の要件は,$a$,$m$が正で互いに素であることでしたから,$B$が正,かつ$B$と$m$が互いに素であるという条件下で「$\varphi(m)=l_{a}l_{b} – 1$」となる$l_a$と$l_b$を作ることができるということを示せば,式(7)が成立していることを示すことができます。
さて,「$\varphi(m)=l_{a}l_{b} – 1$」を式変形してみましょう。
\begin{eqnarray}
l_{a}l_{b} – \varphi(m) = 1
\end{eqnarray}
その通りです。しかし,$\varphi(m)$に係数がかかっていないので定理を適用することができません。そこで,式(10)をいじってから式を変形していくことにします。$w (≠0)$を利用して,式(10)の両辺を$\frac{1}{w}$乗してみます。
\begin{eqnarray}
B^{\frac{l_{a}l_{b} – 1}{w}}\equiv1\ ({\rm mod}\ m)
\end{eqnarray}
この状態で,先ほどと同じような操作をすると,以下の等式が得られます。分かりやすいように,$-w$を$v$とおくことにします
\begin{eqnarray}
l_{a}l_{b} – \varphi(m)w = 1
\end{eqnarray}
\begin{eqnarray}
l_{a}l_{b} + \varphi(m)v = 1
\end{eqnarray}
見事,式(4)の形と一致しました。ここで,1つ問題があります。式(4)と見比べる時に,$l_a$と$l_b$のどちらを$u$とみなすかという問題です。これは,$l_a$と$l_b$の意味をよく考えれば分かります。公開するのは$l_b$の方です。ですので,式(14)の要件を満たす形で$l_b$を決めてから,式(14)に当てはめて$l_a$を求めて復号のための秘密鍵$s$とすればよいのです。
式(14)の要件というのは「$l_b$と$\varphi(m)$が互いに素」という条件でしたから,そのように$l_b$を定めればよいということになります。ちなみに,$l_a$に関しては「$l_a>0$」という要件が残っています。これに関して証明を加えておきます。つまり,式(14)を満たす$l_a(>0)$が存在することを示します。
式(14)を満たす整数$l_a$と$v$は定理より見つかりますから,適当に見つけたとします。それらを$l_{a_0}$,$v_0$と置きます。このとき,以下が成り立ちます。
\begin{eqnarray}
l_{b}l_{a_0} + \varphi(m)v_0 = 1
\end{eqnarray}
式(15)を整数nを利用して少しいじると
l_{b}(l_{a_0} + \varphi(m)n) + \varphi(m)(v_0 – l_{b}n) = 1
\end{eqnarray}
$A$:$B^{l_a}\ ({\rm mod}\ m)$
$B$:$A^{l_b}\ ({\rm mod}\ m)$
$p$:大きな素数→適当に作る
$q$:大きな素数→適当に作る
$l_b$:暗号化のための定数→$\varphi(m)$と互いに素
$l_a$:復号のための定数→式(14)を満たす形で決定
$m$:公開鍵の要素→$p$と$q$から計算
$k$:公開鍵→決まる
$s$:秘密鍵→$l_a$と同じ
心配いりません。$\varphi(m)$は$m=pq$より小さい正の整数のうち,$m=pq$と互いに素な数の個数を表しているのでした。$p$と$q$は素数ですので,$m$より小さな$m-1$個の正数から,$p$の倍数と$q$の倍数の数を引けばよいです。
$m$よりも小さな$p$の倍数は,$p,2p,\ldots,(q-1)p$の$q-1$個です。同様に,$m$よりも小さな$q$の倍数は,$q,2q,\ldots,(p-1)p$の$p-1$個です。以上から,$\varphi(m)$を計算することができます。
\begin{align}
\varphi(m) &= (pq-1)-(q-1)-(p-1) \\
&= pq-p-q+1 \\
&= (p-1)(q-1)
\end{align}
ちなみに,RSA暗号の説明の中には,$p-1$と$q-1$の最小公倍数を用意するものもあります。これは,$\varphi(m)$と互いに素な整数$l_b$を探すという$\varphi(m)$本来の役割に着目したものです。$l_b$を探す場面に限定すれば,$p-1$と$q-1$の最小公倍数$L$を考えれば十分だからです。
\begin{eqnarray}
L = \rm{lcm}[p-1, q-1]
\end{eqnarray}
ただし,$\rm{lcm}[\alpha, \beta]$は$\alpha$と$\beta$の最小公倍数を表します。このとき,整数$k$を用いて$\varphi(m)$は以下のように表されます。
\begin{align}
\varphi(m) &= kL
\end{align}
式(14)に代入すると,以下が得られます。
\begin{align}
l_{a}l_{b} + kLv &= 1 \\
l_a l_b + Lv &= 1
\end{align}
ただし,$kv$を改めて$v$と置き直しました。以上の議論から,RSAの定式化において$\varphi(m)$の代わりに$L$を考えても破綻しないことが分かりました。逆に言えば,わざわざ最小公倍数を持ち込まなくてもRSAの定式化は可能ですが,一般に$p-1$と$q-1$の積を取ると桁数が大きくなってしまうため,計算を簡単にするという観点から$\varphi(m)$ではなく$L$が好んで利用されるようです。
いい指摘です。$l_a$の存在は示せましたが,それを実際に計算で求めることは可能なのかという疑問ですね。これについては,「係数が互いに素である一次不定方程式はユークリッド互除法を利用して解を求めることができる」という定理があります。そちらを利用すれば,ユークリッドの互除法を計算方法として利用して$l_a$を求めることができることが分かりました。
具体的には,式(14)「$l_{a}l_{b} + Lv = 1$」を満たす$l_a$を求めればよいのですが,$v$は途中で途中で勝手に定めた定数ですので,modを利用してvを無くします。すなわち,
\begin{eqnarray}
l_{a}l_{b} \equiv 1\ \rm{mod}\ L
\end{eqnarray}
を満たす形で$l_a$を決定すればよいことになります。これにて,RSA暗号化方式の証明が完了しました。
RSAの流れ再確認
 RSAの流れ
RSAの流れ1.定数の設定
$p$:大きな素数を適当に作る
$q$:大きな素数を適当に作る
$m$:公開鍵の要素→$p$と$q$から計算
$L$:$\rm{lcm}[p-1, q-1]$として定める
$l_b$:$L$と互いに素となるように作る
$l_a$:「$l_{a}l_{b} \equiv 1\ \rm{mod}\ L$」を満たす形で決定
$k$:$l_b$と$m$によって定まる
$s$:$l_a$と同じ
2.暗号化と復号
$A$:$B^{l_a}\ ({\rm mod}\ m)$
$B$:$A^{l_b}\ ({\rm mod}\ m)$
実際に,簡単な素数を用いて公開鍵を暗号鍵を生成してみましょう。まず,自分で定めるのは$p$と$q$でした。ここでは,簡単に$p=17, q=19$としましょう。続いて,公開鍵の要素である$m$を求めます。$p$と$q$の積ですので,$323$と求められます。
続いて,$p-1$と$q-1$の最小公倍数である$L$を求めましょう。$L=\rm{lcm}[16, 18]=144$となります。
次に求めるのは,$l_b$です。$l_b$は$L$と互いに素であればOKですから,その中で一番小さな値を設定しましょう。つまり,$l_b=5$です。$l_b$が求まりましたので,$l_a$も求めることができます。$l_{a}l_{b} \equiv 1\ (\rm{mod}\ L)$を満たすように$l_a$を設定しましょう。
$l_b$と$L$を代入すれば,$l_{a}\cdot 5 \equiv 1\ (\rm{mod}\ 144)$となります。これを満たす$l_a$は,最も簡単な候補としては$144/5 + 1 \fallingdotseq 29$ となります。実際に,$l_a = 29$を$l_{a}\cdot 5 \equiv 1\ (\rm{mod}\ 144)$に代入してみると,$29 \cdot 5 = 145 \equiv 1\ (\rm{mod}\ 144)$となり,確かに成立していることが分かります。以上で,公開鍵と秘密鍵の生成は完了しました。
【生成された鍵ペア】
●公開鍵:$l_b = 5, m=323$
●秘密鍵:$l_a = 29$
実際に確認してみる
以上の設定を用いて,平文$A=10$を暗号化し,復号してみましょう。暗号化の式から,
\begin{eqnarray}
B=10^{5}\;({\mathrm mod}\;323)=193
\end{eqnarray}
となります。また,復号化の式に従って計算を行うと,
\begin{eqnarray}
193^{29}\;({\mathrm mod}\;323)=10
\end{eqnarray}
となり,元の平文$10$が復号されることが確認できました.
ひとこと
非常にややこしい分野でした。多くの人が,「RSAは桁数の大きい素因数分解が大変であること」を利用していることは知っているかと思います。しかし,ここまで踏み込んで理解している人はごく少数だと思われます。個人的に美しいのが,暗号化にまでも「オイラーの定理」が応用されていることです。「数学が役に立つ例」として非常に分かりやすいのは今回のRSAではないでしょうか。















コメント失礼します。大変わかり易い解説ありがとうございます。1点だけ、なぜφ(m)がmより小さい正の整数の積の最大公約数となるのか、何度読み返しても理解できませんでした。可能であれば補足説明して頂けないでしょうかm(_ _)m
tanaka様
ご連絡ありがとうございます。
本記事はかなり前に執筆した文章でして,誤植が多く大変失礼いたしました。
自分の理解が間違えていたため,本文を修正しました。
他にも,modがローマン体になっていないなど,数式として不適切な表記も混在していますが,何卒ご容赦ください。
早速のご回答と訂正ありがとうございます。腹落ちさせる事ができ、スッキリしました。大変勉強になりました。ありがとうございました。
度々申し訳ありません。φ(m)をp-1とq-1の最小公倍数に置き換える事ができる理由について、補足説明して頂く事は出来ませんでしょうか?お時間ある時で結構ですので、どうか宜しくお願い致します。
tanaka様
ご質問ありがとうございます。
本文を加筆してみました!書き殴りで恐縮ですが,これで疑問は解決できそうでしょうか??
ありがとうございます!色んなサイトを見ましたが、最小公倍数を使う理由がイマイチ説明されておらず、質問させて頂きました。(p-1)(q-1)より、lcm[p-1,q-1]の方が、lbを探す手間が省けると言う理解で合ってますでしょうか??
丁寧な補足のご説明、ありがとうございました。疑問が解消され、腹落ちさせることができました。本当にありがとうございましたm(_ _)m
tanaka様
ご返信が遅れてしまい大変申し訳ありません!
正確なことは言えないのですが,恐らくオーバーフロー対策として最小公倍数を用いるものと思われます。
以下のopensshの実装を覗いてみると,どのようにrsaが実装されているのかが理解でき,計算量やオーバーフロー等の観点も理解しやすいかと思われます。
https://github.com/openssh/openssh-portable/blob/master/ssh-keygen.c
こちらでは確認する時間が取れず恐縮ですが,参考にしていただければと思います。