pythonで簡単な音声認識をやってみたいぞ。
そもそも何から始めればいいのかしら。
今回は,基本的な音声認識をpythonで行う方法をお伝えしていこうと思います。本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。

【超初心者向け】python入門講座/実践講座まとめ目次
入門講座
1.実行環境2.文字の出力3.データ型4.変数5.更新と変換6.比較演算子7.論理演算子8.条件分岐9.リスト10.辞...
スポンサーリンク
読みたい場所へジャンプ!
お題
DFTをpythonで実装してみよう。
流れ
今回対象とするデータは「あいうえお」ではなく,データ長が1024である合成サイン波とします。なぜなら,DFTのデータ長が2のべき乗のときに,効率的な再帰計算により高速フーリエ変換が可能になるからです。
実際に合成サイン波を作ってみましょう。
import numpy as np
import matplotlib.pyplot as plt
# データ長
N = 128
x = np.arange(N)
# 周期
t1 = 10
t2 = 20
t3 = 30
# 3つの周期の重ね合わせ
y = np.sin(t1 * 2 * np.pi * (x/N)) + np.sin(t2 * 2 * np.pi * (x/N)) + np.sin(t3 * 2 * np.pi * (x/N))
# 可視化
plt.plot(x, y)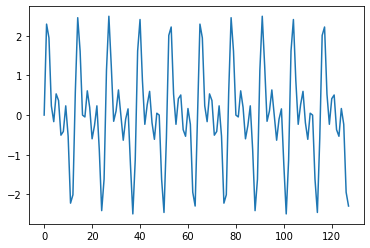
DFT(離散フーリエ変換)
離散フーリエ変換の式は以下の通りです。詳しい導出は省略します。こちらの資料[やる夫で学ぶディジタル信号処理]がおすすめです。
\begin{eqnarray}
X[\omega] &=& \sum_{n=0}^{N-1} x[n] e^{-i\frac{2\pi \omega n}{N}}
\end{eqnarray}
実装
この式を愚直に実装していきましょう。
import numpy as np
def DFT(x):
# 結果を格納するリスト
X = []
# データ長
length = x.shape[0]
# データ長だけ繰り返します
for n in range(length):
# x[n]に掛け合わせる部分です
weight = np.exp(-1j*((2*np.pi*n)/length))
# シグマの部分です
X_omega = 0
for omega in range(length):
X_omega += x[omega] * (weight**omega)
X.append(X_omega)
return np.array(X)結果
# 実行
Y = DFT(y)
# 結果は複素数なので実部と虚部に分けて可視化
Y_real = np.abs(Y)
Y_imag = np.imag(Y)
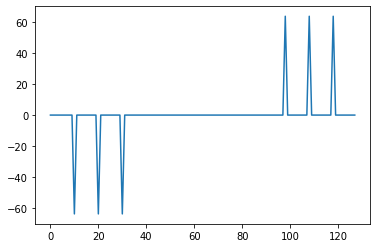
plt.plot(np.arange(0, Y_real.shape[0]), Y_real)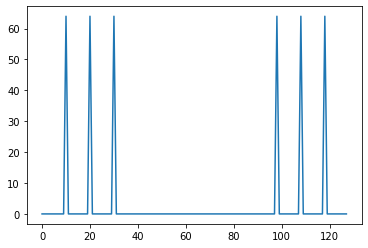
plt.plot(np.arange(0, Y_real.shape[0]), Y_imag)