【超初心者向け】自己回帰モデルをpythonで実装してみた。

今回は，scikit-learnなどの既成ライブラリにできるだけ頼らずに，自己回帰モデルを実装していきたいと思います。また，本記事はpython実践講座シリーズの内容になります。その他の記事は，こちらの「Python入門講座/実践講座まとめ」をご覧ください。

自己回帰モデル

こちらの記事で詳しく説明しています。

【サーベイまとめ】自己回帰モデルとは？係数の求め方まで出来る限り分かりやすく簡潔に説明します。この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多...

 

問題設定

今回は，気象庁より直近の過去1年分の平均気温をデータセットとして利用したいと思います。（気象庁のHPはコチラから）

具体的には，2018/6/10から2019/6/10までの平均気温を利用します。次数は$2$として設定します。つまり，2日前までの平均気温データを利用してモデルを構築していくという意味です。

コード解説

以下では，コードの意味を解説していきたいと思います。係数の導出方法などは，先ほど紹介した記事でお伝えしていますので，適宜参考にしてみてください。

必要なライブラリ等のインポート

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib.dates as dates
import numpy.linalg as LA
import datetime as dt
from pandas.plotting import register_matplotlib_converters

必要なライブラリ等をインポートします。

データの読み込み

df = pd.read_csv('data.csv')
header = df.columns.values.tolist()
data = df.values

データを配列に格納します。この際，ヘッダーとデータ（日付，数値）は別々にしておくことで扱いやすくなります。

格納したデータの確認

print(header)
print(data[:5])

['date', 'tempreture']
[['2018/6/10' 21.3]
 ['2018/6/11' 22.9]
 ['2018/6/12' 21.4]
 ['2018/6/13' 20.2]
 ['2018/6/14' 21.1]]

このような形でデータが格納されています。

データの可視化

x_list = np.array([dt.datetime.strptime(data[:,0][i], '%Y/%m/%d') for i in range(data.shape[0])])

fig, ax = plt.subplots(figsize=(12, 8))

ax.plot(x_list, data[:,1])
plt.xticks(rotation=90)
ax.xaxis.set_major_locator(dates.MonthLocator())
ax.xaxis.set_major_formatter(dates.DateFormatter('%Y/%m'))
register_matplotlib_converters()
plt.show()

データを可視化して確認します。夏は暑く，冬は寒くなっていることが確認できます。読み取ったデータ内の日付を「文字列→datetime型」に変換してから，monthlocatorを利用して，x軸のラベルをうまく設定していきましょう。正直に日付けだけを表示しようとすると，真っ黒になります。

時系列データの格納

y = np.array(data[:,1])

y_1 = y
y_1 = np.insert(y_1, 0, 0)
y_1 = np.delete(y_1, y_1.shape[0]-1)

y_2 = y_1
y_2 = np.insert(y_2, 0, 0)
y_2 = np.delete(y_2, y_2.shape[0]-1)

phi_0 = np.mean(y*y)
phi_1 = np.mean(y*y_1)
phi_2 = np.mean(y*y_2)

愚直なコーディングですが，時系列データを$y$に格納し，1日ずつずらして$y_1, y_2$に格納します。こうすることで，自己相関$\phi$を計算しやすくしています。

テプリッツ行列の作成

Phi = np.zeros(4).reshape((2,2))
phi_list = np.array([phi_0, phi_1])
for i in range(2):
  Phi[i,i] = phi_list[0]

for i in range(1):
  Phi[i, i+1] = phi_list[1]
  Phi[i+1, i] = phi_list[1]

一応，次数が大きくなった場合でも利用できるように，for文で書きました。

係数を求める計算

Phi_list = np.array([phi_1, phi_2])
A = LA.inv(Phi) @ Phi_list.T

二乗誤差が最小となるように，係数を定めていきます。

予測データの可視化

y_list = (A[0]*y_1 + A[1]*y_2)

fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(x_list[2:], data[:,1][2:])
ax.plot(x_list[2:], y_list[2:])
plt.xticks(rotation=90)
ax.xaxis.set_major_locator(dates.MonthLocator())
ax.xaxis.set_major_formatter(dates.DateFormatter('%Y/%m'))
plt.show()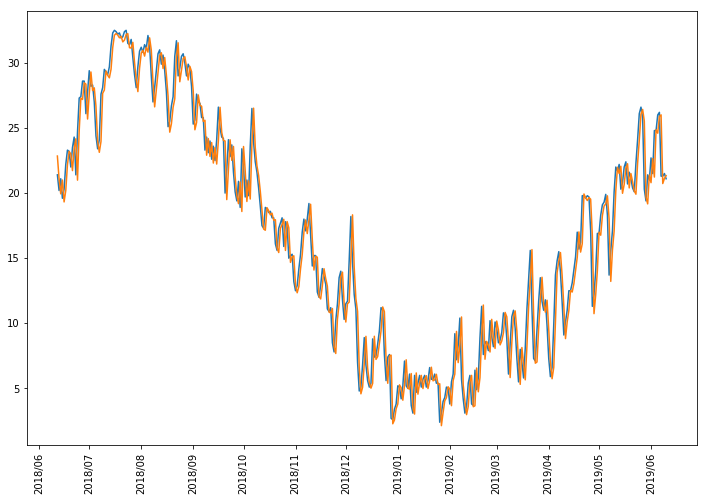

予測されたデータを可視化します。一点注意点として，計算されたデータの3つ目から表示させている点です。これは，次数が$2$であることが理由です。2日前までのデータを利用するということは，2018/6/10と2018/6/11は予測するためのデータが手元に無いので予測できないからです。ですので，3つ目の予測結果である2018/6/12より出力しています。

もし理論にモヤモヤがあれば

こちらの参考書は，PRMLよりも平易に機械学習全般の手法について解説しています。おすすめの１冊になりますので，ぜひお手に取って確認してみてください。

全コード

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib.dates as dates
import numpy.linalg as LA
import datetime as dt
from pandas.plotting import register_matplotlib_converters

df = pd.read_csv('data.csv')
header = df.columns.values.tolist()
data = df.values

print(header)
print(data[:5])

x_list = np.array([dt.datetime.strptime(data[:,0][i], '%Y/%m/%d') for i in range(data.shape[0])])

fig, ax = plt.subplots(figsize=(12, 8))

ax.plot(x_list[2:], data[:,1][2:])
plt.xticks(rotation=90)
ax.xaxis.set_major_locator(dates.MonthLocator())
ax.xaxis.set_major_formatter(dates.DateFormatter('%Y/%m'))
register_matplotlib_converters()
plt.show()

y = np.array(data[:,1])

y_1 = y
y_1 = np.insert(y_1, 0, 0)
y_1 = np.delete(y_1, y_1.shape[0]-1)

y_2 = y_1
y_2 = np.insert(y_2, 0, 0)
y_2 = np.delete(y_2, y_2.shape[0]-1)

phi_0 = np.mean(y*y)
phi_1 = np.mean(y*y_1)
phi_2 = np.mean(y*y_2)

Phi = np.zeros(4).reshape((2,2))
phi_list = np.array([phi_0, phi_1])
for i in range(2):
  Phi[i,i] = phi_list[0]

for i in range(1):
  Phi[i, i+1] = phi_list[1]
  Phi[i+1, i] = phi_list[1]

Phi_list = np.array([phi_1, phi_2])
A = LA.inv(Phi) @ Phi_list.T

y_list = (A[0]*y_1 + A[1]*y_2)

fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(x_list[2:], data[:,1][2:])
ax.plot(x_list[2:], y_list[2:])
plt.xticks(rotation=90)
ax.xaxis.set_major_locator(dates.MonthLocator())
ax.xaxis.set_major_formatter(dates.DateFormatter('%Y/%m'))
plt.show()