今回は,scikit-learnなどの既成ライブラリに頼らずにロジスティック回帰に基づく二値分類を実装していこうと思います。また,本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。
データセット
今回は,分かりやすさを重視して,scikit-learnのメソッドを利用して線形分離可能なデータセットを作成します。また,パーセプトロン学習規則による二値分類の際にも利用したデータセットなので,比較がしやすいというメリットもあります。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
x_train, t_train = make_blobs(random_state=8, n_samples=50, n_features=2, cluster_std=1.5, centers=2)
N = x_train.shape[0] # サンプル数
D = x_train.shape[1] # 特徴数
ones = np.ones(N)
x_train = np.hstack([np.array([ones]).T, x_train])plt.scatter(x_train[:, 0], x_train[:, 1], marker='o', c=t_train)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")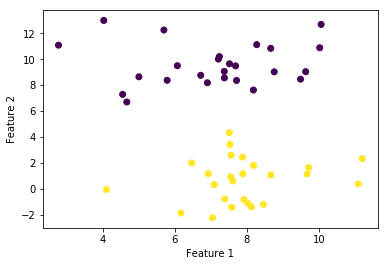
重みのバイアス項を作るために,すべての要素が1の行列をx_trainの左側からくっつけます。また,t_trainは,x_trainのラベルとして与えられています。
コード
以下では,まず部分的にコードの解説をした後に,全体のコードをお伝えしたいと思います。
識別関数の定義
def Phi(w, x):
phi_x = w.T @ x
return phi_x今回の識別関数は,重みパラメータとデータの内積で与えることにします。つまり,単項式回帰と同様に識別面は直線になるということです。
シグモイド関数の定義
def Sigmoid(w, x):
phi_x = Phi(w, x)
sigm_x = 1/(1+np.e**(-phi_x))
return sigm_xシグモイド関数の定義から,関数を作ってしまいます。
重みの最適化
def OptimalWeight(w, x, t, c):
sigm_x = Sigmoid(w, x)
w_opt = w - c * (sigm_x - t) * x
return w_opt最急降下法のアイディアにより,重みを最適化していきます。パーセプトロンの学習規則とは異なり,モデルの出力が$\{ 0, 1 \}$の確率値で与えられるため,正しく識別出来ている場合でも重みパラメータを更新します。
メイン部分
# N: サンプル数
# D: 特徴数
N = x_train.shape[0]
D = x_train.shape[1]
w_init = np.zeros(D).T
w_init[0] = 1
w_opt = w_init
c = 0.1
iter = 100
for i in range(iter):
for n in range(N):
w_opt = OptimalWeight(w_opt, x_train[n, :], t_train[n], c)NとDを新しく取得した後に,重みの初期値を設定しています。今回は,単純に全て0に設定しました。また,初期値にバイアスが上手く作用するように,重みパラメータのインデックス0を1にしています。繰り返しの部分では,適当に更新回数を100回にしました。また,適当に学習係数は0.1にしました。
グラフ出力の準備
# w_1*x_1 + w_2*x_2 + w_3*x_3 = 0
# x_3 = -(w_1*x_1 + w_2*x_2) / w_3
xlist = np.arange(np.min(x_train[:, 1]), np.max(x_train[:, 1]), 0.1)
ylist = -(w_opt[0]*1 + w_opt[1]*xlist) / w_opt[2]コメントでも記してありますが,$w_1 x_1 + w_2 x_2 + w_3 x_3 = 0$が識別面の関数なので,$x_3 = -\frac{w_1 x_1 + w_2 x_2}{w_3}$と変形することによりxlistに対する出力であるylistを得ることができます。
グラフ出力
plt.plot(xlist, ylist)
plt.scatter(x_train[:, 1], x_train[:, 2], marker='o', c=t_train)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()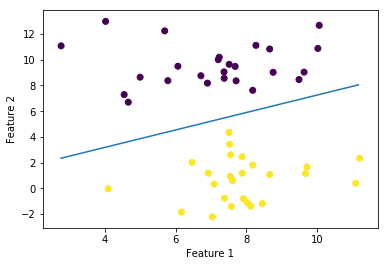
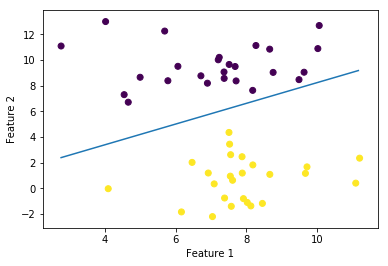
ちなみに,パーセプトロン学習規則による識別面は以下の通りです。
考察
パーセプトロンの学習規則に基づく手法よりも,妥当な分離面が作られていることが読み取れます。これは,パーセプトロンの学習規則が一度収束したらそこから動かないという性質をもっているのに対し,ロジスティック回帰のモデルは分類を確率値として与えるため,たとえ正しく分離される面が得られたとしても,より良く識別できるように更新されていくからです。
もし理論にモヤモヤがあれば
(2026/01/31 02:57:33時点 楽天市場調べ-詳細)
こちらの参考書は,誰もが挫折しかけるPRMLよりも平易に機械学習全般の手法について解説しています。おすすめの1冊になりますので,ぜひお手に取って確認してみてください。
全体のコード
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
def Phi(w, x):
phi_x = w.T @ x
if phi_x > 0:
disc = 1
else:
disc = -1
return [phi_x, disc]
def OptimalWeight(w, x, t, c):
phi_x, disc = Phi(w, x)
if disc * t > 0:
w_opt = w
else:
w_opt = w + (c * t * x)
return [w_opt, disc*t]
x_train, t_train = make_blobs(random_state=8,
n_samples=50,
n_features=2,
cluster_std=1.5,
centers=2)
N = x_train.shape[0]
D = x_train.shape[1]
ones = np.ones(N)
x_train = np.hstack([np.array([ones]).T, x_train])
t_train = np.where(t_train==0, -1, t_train)
plt.scatter(x_train[:, 1], x_train[:, 2], marker='o', c=t_train)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
N = x_train.shape[0]
D = x_train.shape[1]
w_init = np.zeros(D).T
w_opt = w_init
Disc = np.zeros(N)
iter = 100
for i in range(iter):
for n in range(N):
w_opt, Disc[n] = OptimalWeight(w_opt, x_train[n, :], t_train[n], c=0.5)
if all([e>0 for e in Disc]):
break
xlist = np.arange(np.min(x_train[:, 1]), np.max(x_train[:, 1]), 0.1)
ylist = -(w_opt[0]*1 + w_opt[1]*xlist) / w_opt[2]
plt.plot(xlist, ylist)
plt.scatter(x_train[:, 1], x_train[:, 2], marker='o', c=t_train)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()