【超初心者向け】損益分岐点とは？公式の覚え方を分かりやすく解説します！Beginaid

本記事は教養記事シリーズその３７です。その他の教養記事はコチラの目次をご覧ください。

★この記事の流れ★

損益分岐点とは？
公式は？
覚え方は？

本記事は初学者の理解を優先しているため正確性に欠ける場合があります。致命的なミスはご指摘いただけますと助かります。

損益分岐点とは

「そんえきぶんきてん」…？

どういう意味…？

損益分岐点というのは，売上高と費用が一致する値のことを指します。

特に，売上高の値のことを「損益分岐点売上高」と呼びます。

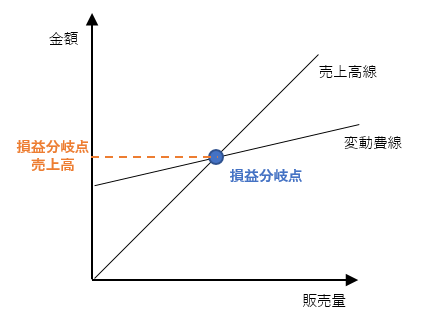損益分岐点

こんな例を考えてみましょう。Aさんはリンゴ屋を営んでいます。Aさんのお店は月１０万円の売り上げがありました。このとき，アルバイト代や土地代などの諸経費で月１０万円かかってしまったとします。この状況が，まさに収益分岐点が表す状態です。赤字でもなく，黒字でもない状況です。

公式

【収益分岐点売上高の公式】

\begin{eqnarray}
収益分岐点売上高＝\frac{固定費}{１－\frac{変動費}{売上高}}
\end{eqnarray}

…ナニコレ？

こんな公式覚えられませんよね。そこで，今回は収益分岐点売上高とはそもそも何だったかから考えて公式を導いてみたいと思います。普通であれば，１次関数でグラフ上の交点を求めることで式（１）のような公式が求められます。しかし，ここでは簡単な式変形だけで公式を理解することができることを示します。売上高と費用が同じとき，黒字でもなく赤字でもありません。

\begin{eqnarray}
（売上高）＝（費用）
\end{eqnarray}

このような状況の売上高を「収益分岐点売上高」と呼ぶのでした。

\begin{eqnarray}
（収益分岐点売上高）＝（費用）
\end{eqnarray}

費用というのは，固定費と（損益分岐点における）変動費に分けられます。

\begin{eqnarray}
（収益分岐点売上高）＝（固定費）＋（損益分岐点における変動費）
\end{eqnarray}

●固定費：土地代や人件費など
●変動費：材料費など

式（４）を変形していくだけで，公式を導くことができます。

\begin{eqnarray}
（収益分岐点売上高）-（損益分岐点における変動費）&＝&（固定費）\\
（収益分岐点売上高）\{１－\frac{（変動費）}{（売上高）} \}&=&（固定費）\\
（収益分岐点売上高）&＝&\frac{（固定費）}{１－\frac{（変動費）}{（売上高）}}
\end{eqnarray}