pythonで簡単な音声認識をやってみたいぞ。
そもそも何から始めればいいのかしら。
今回は,基本的な音声認識をpythonで行う方法をお伝えしていこうと思います。本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。

読みたい場所へジャンプ!
お題
F0推定をpythonで実装してみよう。
流れ
今回対象とするデータは「あいうえお」ではなく,データ長が2をべき乗に制限した「ドレミファソラシド」にしようと思います。以下のファイルを対象とします。
F0推定の概要
F0は基本周波数とも呼ばれており,音楽でいうところの音高(ピッチ)に相当します。ごく基本的な音声認識の特徴量としても利用されます。さて,基本周波数はどのように推定すれば良いのでしょうか。
ここでポイントとなるのが「自己相関(AutoCorrelation)」です。結論から言うと,自己相関のピークを捉えることで基本周波数を(近似)推定することができます。自己相関は,以下の式で計算していきます。$x$をある信号とします。
\begin{eqnarray}
\rm{AutoCorrelation} &=& \sum_{t=0}^{N – \tau – 1}x_{t}x_{t+\tau}
\end{eqnarray}
数式上ではイメージが掴みにくいと思います。自己相関は,自分自身の信号を複製し,1フレームずつズラしながら掛けて足し合わせるという操作で計算していきます。そのときのズレが「$\tau$」となります。
どんなときに自己相関は大きくなるのでしょうか。最もわかりやすいのは$\tau=0$のときです。自分自身と掛け合わせるのが一番大きな自己相関になるのは想像がつきやすいです。さて,二番目に大きな自己相関は$\tau$がどのような値の時でしょうか。
そうです。二番めに大きなピークを与える$\tau$こそ「基本周期」なのです。つまり,基本周波数(F0)の逆数に相当します。以下では,自己相関を求めて二番目のピークを与える$\tau$を計算することで,基本周波数を近似推定していきます。ちなみに,STFTのときと同じように,元の信号に窓をかけながらステップごとに自己相関を計算していきます。
実装
必要なライブラリのインポート
import numpy as np
import librosa
import matplotlib.pyplot as plt
import librosa
import librosa.displaywavファイルの読み込み
# [path_to_wavfile]にはみなさんの環境に合わせたパスを入れてください
y, sr = librosa.load("[path_to_wavfile]")自己相関の定義式
def AutoCorrelation(y, lim):
# 一応上限にlimという引数を与えています。
# 窓で切り出す場合は特に必要ないかもしれません。
AC = []
for i in range(lim):
if i==0:
# スライスで指定するときの例外処理
AC.append(np.sum(y*y))
else:
# 元の信号とコピーをズラしながら掛け合わせていきます
# 格納する値は足し合わせたものです
AC.append(np.sum(y[0:-i] * y[i:]))
return np.array(AC)ピークの判定
ここでは「ピーク」からデータの先頭・末尾をのぞいています。なぜなら,自己相関において先頭は「一番大きなピーク」を持つことが自明だからです。こうすることで,算出されたピークのうち最も大きな点を探し出せば良いというシンプルな問題に帰着できます。
def detect_peak(AC):
peak = []
# 最初と最後はピークから除きます
for i in range(AC.shape[0]-2):
if AC[i]<AC[i+1] and AC[i+1]>AC[i+2]:
peak.append([i+1, AC[i+1]])
return np.array(peak)フレームごとに自己相関を算出する
def calc_AC(x, win_length, hop_length, sr):
# 算出値を格納する箱
second_peak_indexes = []
# データのサンプル数
N = x.shape[0]
# 窓を適用する回数
T = int((N - hop_length)/hop_length)
for t in range(T):
# 窓で切り出されたデータ
x_this = x[t*hop_length:t*hop_length+win_length]
# 自己相関を計算
AC = AutoCorrelation(x_this, x_this.shape[0])
# ピーク候補を絞る
peak = detect_peak(AC)
peak_index = peak[:, 0]
peak_value = peak[:, 1]
# 値の大きい順にソート
peak_value_sorted = np.sort(peak_value)[::-1]
# 先頭を取ってくる(np.maxを利用してもOK)
second_peak_value = peak_value_sorted[0]
# 最大値のインデックスを取る
second_peak_index = np.where(AC==second_peak_value)[0]
# 結果にインデックスを格納
# そのときサンプリング周波数を基本周期で割ることで基本周波数に変換しておく
second_peak_indexes.append(sr/second_peak_index[0])
return np.array(second_peak_indexes)先頭と末尾の調整
STFTでは関数内でデータの先頭と末尾の調整をしました。窓関数を適用するときには避けては通れない調整(地獄)です。今回は単純に,推定された先頭の値をデータの先頭で推定された周波数,末尾の値をデータの末尾で推定された周波数と補完することにします。
ここ,説明が難しいです。本来であれば,先頭のデータから窓関数を適用していかなくてはならないのですが,先頭から適用すると窓関数の半分がはみ出てしまうため,はみ出ない位置から始めていたのです。末尾も同様です。補完のコードは以下の通りです。
second_peak_indexes = np.concatenate([[second_peak_indexes[0]], second_peak_indexes, [second_peak_indexes[-1]]])可視化
自己相関のイメージを掴んでもらうために,wavファイルを大きな1つのデータとして捉えて自己相関を可視化してみます。
AC = AutoCorrelation(y, 3000)
plt.plot(np.arange(AC.shape[0]), AC)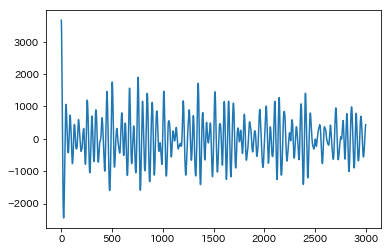
スペクトログラム上に可視化
それではクライマックスです。スペクトログラム上に推定された基本周波数を乗せてみましょう。扱うスペクトログラムは「ドレミファソラシド」です。
spec = librosa.stft(y, win_length=1024, hop_length=512)
spec_db = librosa.amplitude_to_db(np.abs(spec))
librosa.display.specshow(spec_db, y_axis="log")
仮説を立てるとすれば,スペクトログラム上で濃い色になっている部分が基本周波数だと考えられます。これはピアノの音ですから,倍音成分を持っています。つまり,一番濃い部分に対して,周波数は2倍,3倍…の成分を持ちます。
さて,正解発表です。
librosa.display.specshow(spec_db, y_axis="log", cmap="gray_r")
plt.plot(np.arange(spec_db.shape[1]), second_peak_indexes, color="r", linewidth = 2.0)
見事に仮説通りになりました!今回はピアノだけの「ドレミファソラシド」という単純なデータを扱っていたため簡単に推定できたのだと思います。