今回は,機械学習や統計学の代表的な評価指標であるF値に関する解説とPythonで実装する方法をお伝えしていこうと思います。本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。

読みたい場所へジャンプ!
F値の概要
F値は,2つの評価指標を踏まえた統計的な値です。結論からお伝えすると,以下のような式でF値を求めることができます。
\begin{eqnarray}
F &=& \frac{2}{\frac{1}{P}+\frac{1}{R}}
\end{eqnarray}
これを見てもサッパリだと思います。ですので,この記事の目標はF値の式を見て「何を表しているのか」という点が理解できるようになることを目指します。他にも,各指標を効果的に理解する方法をお伝えしていこうと思います。
問題設定
機械学習の代表的なタスクとして,分類タスクが挙げられます。一般的な言い方をすれば「あるデータがいくつかのクラスのうちいずれに属すかを判断する」という問題設定になります。
しかし,F値をはじめとする機械学習で用いられる評価指標では二値分類タスクを前提としているものが多いです。二値分類タスクを前提としても,多値分類タスクに拡張することは難しくないため,以下では二値分類タスクを想定して話を進めていきます。
二値分類タスクの評価指標を考えるとき,非常に有効な手段があります。「分割表(混同行列)」です。二値を「正・負」で表して,一方の軸に「実際の正負」,もう一方の軸に「機械学習により推定された正負」を設定します。
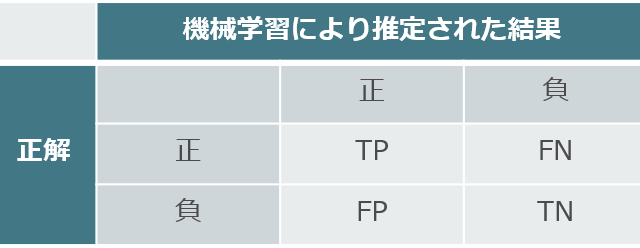 分割表(混同行列)
分割表(混同行列)分割表には「TP・TN・FP・FN」の4つの文字が書いてありますね。基本的に,これらの4つのアイディアを理解できればF値は大体理解できます。しかし,多くの書籍ではこの指標を投げつけるだけ投げつけて放置プレイです。
となってしまうのは当たり前です。そこで,今回はこれらの指標を効果的に理解する方法をお伝えしていこうと思います。まずは,それぞれが英単語の頭文字から取ってきている点を理解してください。
●TP:True Positive
●TN:True Negative
●FP:False Positive
●FN:False Negative
ここまで理解していても,どれが何を表しているのかが覚えきれないという方がたくさんいらっしゃると思います。ここで思い出してほしいのは,今考えているのは何の評価指標なのかということです。私たちは,あくまでも「機械学習モデルの出力する予測」の評価を行いたいのです。
英語圏の人々は,結論から先に話し始めるのは有名な話かもしれません。この評価指標も例外ではありません。まず最初に,機械学習モデルの出力する予測の正誤を言ってしまいます。
●T:合っているよ!
●F:間違えているよ!
そして,そのあとに機械学習モデルが実際に出力した正負(Positive/Negative)を言います。
●P:予測は正だったね!
●N:予測は負だったね!
ここまでをガッチャンすると,以下のように解釈できます。
●TP:予測は合っているよ!君の予想では正だったよね。
●TN:予測は合っているよ!君の予測では負だったよね。
●FP:予測は間違えているよ!君の予測では正だったね。
●FN:予測は間違えているよ!君の予測では負だったね。
少しずつ意味が理解できてきましたか…?それでは,先ほどの分割表に戻ってみましょう。
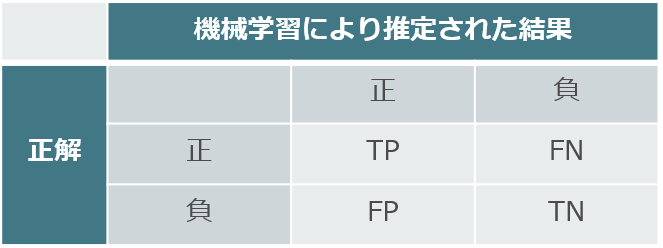
理解の仕方としては,まず合っていて嬉しい2つの指標に注目します。つまり,「TP」と「TN」です。
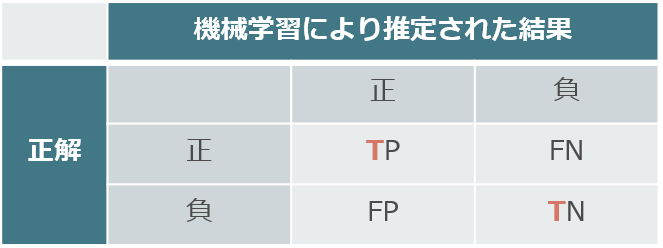 Tは「合っているよ!」という意味
Tは「合っているよ!」という意味続いて,機械学習が出力した正負に注目します。
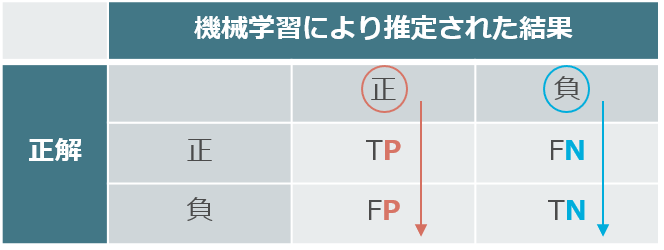 「P」は正,「N」は負を表します。
「P」は正,「N」は負を表します。このようにすれば,大体のイメージはつかめると思います。
おさえておくべき評価指標
これらの4つの値を利用して,いくつかの評価指標を紹介していきます。最後に,F値を説明したいと思います。
正解率(Accuracy)
\begin{eqnarray}
\rm{Accuracy} = \frac{TP+TN}{TP+TN+FP+FN}
\end{eqnarray}
最もベーシックな評価指標です。データ全体に対して,モデルはどれだけ正解できたのかを表す指標です。日本語で説明すると,このようなイメージです。
\begin{eqnarray}
\rm{Accuracy} = \frac{\text{合っているよ!}}{\text{全体}}
\end{eqnarray}
適合率・精度(Precision)
\begin{eqnarray}
\rm{Precision} = \frac{TP}{TP+FP}
\end{eqnarray}
適合度・精度は正と判断したデータのうち実際に正であった割合を示しています。これは,ユーザが利用する検索エンジンを想像すると分かりやすいと思います。つまり,「検索エンジンがユーザーが欲しそうだと思った結果が実際にユーザが欲しい内容だった!」の割合を表しています。
\begin{eqnarray}
\rm{Precision} = \frac{\text{検索エンジンが推定した結果のうち実際にユーザが欲しい結果}}{\text{検索エンジンがユーザが欲しいと推定した結果}}
\end{eqnarray}
再現率(Recall)
\begin{eqnarray}
\rm{Recall} = \frac{TP}{TP+FN}
\end{eqnarray}
再現率は,実際に正であるデータのうちどれだけを正解(再現)できたかの指標です。少し計算式の意味が分かりにくいですよね。ここでは,正を「ガン陽性」と言い換えると分かりやすいと思います。TPは「ガンだと思った患者がガンだった!」を表し,FNは「ガンだと思わなかったけどガンだった…」を表します。日本語で表すと以下のようになります。
\begin{eqnarray}
\rm{Recall} = \frac{\text{ガンだよ!と思って実際にガンだった患者}}{\text{ガン患者全体}}
\end{eqnarray}
1つの疑問
適合率・精度も大切そうですし,再現率も大切そうです。両方ともが最高レベルのモデルなど存在するのでしょうか…?答えは「実際の現場ではNO」です。なぜなら,適合率・精度と再現率はトレードオフの関係にあるからです。
適合率・精度と再現率の違いは何でしょうか?適合率・精度の分母には「FP」がありますね。再現率の分母には「FN」,これはどういうことかというと,機械学習モデルが出力する推定結果のうち間違いを減らすことを考えているということを意味しています。
つまり,「FP(陽性だと思って間違える数)」を減らしたいのが適合率・精度,「FN(陰性だと思って間違える数)」を減らしたいのが再現率ということなのです。理解の仕方のイメージとしては,モデルが正解を出力する信頼度を損ないたくない場合は陰性を陽性と勘違いしたくないため,適合率・精度が重んじられます。一方,陽性が致命的なデータの場合は陽性を陰性と勘違いしたくないため,再現率が重んじられます。
 再現率と適合率・精度
再現率と適合率・精度でもでも。一般の議論では,適合率・精度と再現率の両方を一緒に考えたほうが無難そうですよね。ここでようやく登場するのが「F値」です。
F値
\begin{eqnarray}
\rm{F} &=& \frac{2}{\frac{1}{P}+\frac{1}{R}}\\
&=& \frac{2PR}{P+R}
\end{eqnarray}
F値は,適合率・精度(P)と再現率(R)の調和平均をとったものです。
鋭い突っ込みですね。ここら辺をツッコめるかどうかで今後の理解がかなり違ってくると思います。そもそも,調和平均というのは「割合やパーセンテージ」のような値を同じ対象に用いるときの平均です。例えば,速さの平均などが良い例です。そうです。速さも実は「単位時間当たりどれくらい進めるか」という割合の仲間でした。
例)
太郎君は行きは時速10km,帰りは時速15kmで登校しました。平均の速さはいくつですか。
答1)
学校までの距離を30kmとすると,行きは3時間,帰りは2時間かかることが分かります。つまり,太郎君は合計60kmの道のりを5時間かけて通っているため,平均の速さは$60/5=12$[km/h]です。
答2)
時速の調和平均を取れば$\frac{2\times10\times15}{10+15}=12$[km/h]
ここで単純な算術平均を取ると答えが変わってしまうことに気づきましたか?時速10kmと時速15kmの算術平均は時速12.5kmです。つまり,割合やパーセンテージを扱うとき,同じ対象(今回であれば通学路)を考える場合に調和平均が利用されるということです。
F値の話題に戻りましょう。F値も「適合率・精度や再現率」といった割合やパーセンテージに注目しています。さらに,適合率・精度と再現率は「同じデータ」に対する値であることも前提です。したがって,利用される平均は調和平均が適していると分かります。
実装例
ここでは,scikitlearnを用いたpythonにより実装例を示しておきます。
必要なライブラリのインポート
import numpy as np
from sklearn.metrics import f1_score予測値と正解値のセット
# 今回は両方ともランダムな二値でセット
y_true = (np.random.rand(100)<=0.5)*1
y_pred = (np.random.rand(100)>0.5)*1F値の計算
f_score = f1_score(y_true, y_pred)
print(f_score)Out:
0.5106382978723404どちらともランダムで与えているため0.5になるのは妥当です。
まとめ
F値もなかなか奥が深いです。思考停止状態で「このモデルはF値がいい!最高!」とならないように,しっかりと指標の意味を理解したうえで利用していきたいものです。


















中盤の一文「続いて,機械学習が出力した政府に注目します。」にて、
誤:政府 正:正負
調和平均の式が誤り
分子はこの場合は1段目の式から「2」
とおりすがり様
ご指摘ありがとうございます。修正致しました。
基本的な部分での誤植であったため,非常に助かりました。
positive – negative は 正ー負 というより、肯定 – 否定 といった方がぴったりに感じます。
hendevane様
ご連絡ありがとうございます。
「肯定ー否定」ですか!今までなかった視点で勉強になります。
一方で,機械学習の文脈では「正例・負例」といった用語が使われることや,閾値を利用した判別などもよく行われることなどがら,「正ー負」もそこまで不適切な表現ではないと個人的には考えております。
今後,記事を執筆する際には,hendevane様のご意見を考慮しつつ,用語の選択を行っていきたいと思います。