pythonで簡単な音声認識をやってみたいぞ。
そもそも何から始めればいいのかしら。
今回は,基本的な音声認識をpythonで行う方法をお伝えしていこうと思います。本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。

読みたい場所へジャンプ!
お題
ケプストラムをpythonで抽出してみよう。
流れ
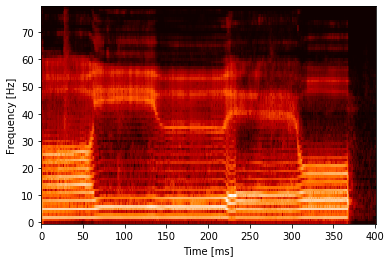
今回対象とするデータは,私が喋った「あいうえお」とします。音声データを貼り付けるのは,どこか恥ずかしさを覚えるため,代わりにスペクトログラムをお見せしておきます。しっかりスペクトロラムに5つの区分が見え,それぞれが「あ/い/う/え/お」に相当することが確認できます。
ケプストラムの概要
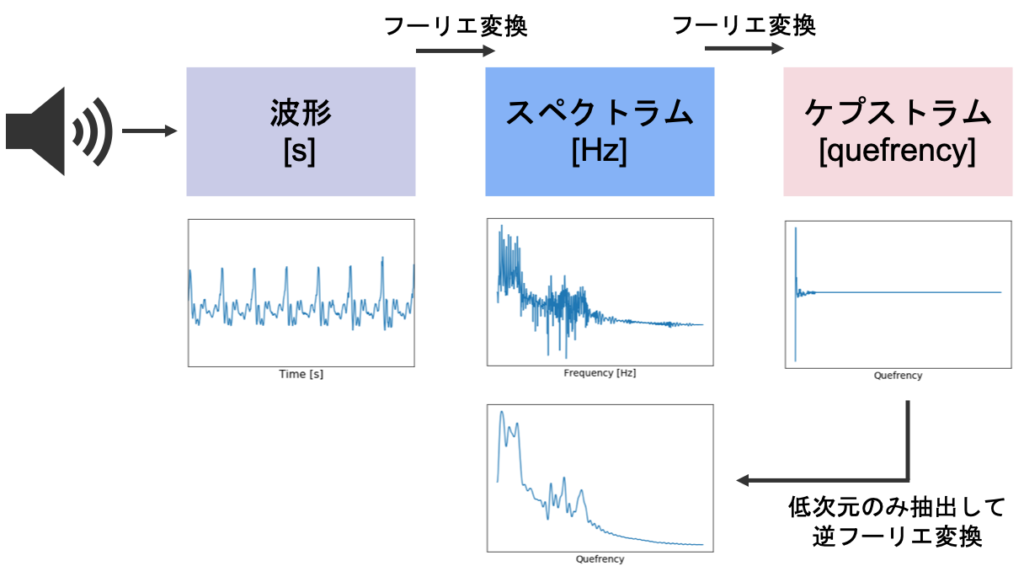
ケプストラムってなに?
ケプストラムは,周波数の周波数です。(少し語弊はあります)
はい?
戸惑うのも無理はないです。ゆっくりお伝えしていきます。ケプストラムの説明には2通りあります。1つめは「対数スペクトルを音声とみなしてフーリエ変換した特徴量」です。これが,先ほどの「周波数の周波数」という説明に繋がります。
もう1つは「対数スペクトルを逆フーリエ変換した特徴量」です。周波数領域のスペクトルを逆フーリエ変換した結果は,時間領域の波形に戻ります。しかし,周波数領域で対数をとっているため,元の波形に戻るわけではないのです。
Web上にはケプストラムの説明として,周波数領域から「フーリエ変換を施したもの」「逆フーリエ変換を施したもの」という2つの説明が氾濫しています。これらは本質的に変わりません。結局,スペクトル包絡を得たいというのがケプストラムのモチベーションです。まれに,対数スペクトルをフーリエ変換することが「間違い」だと勘違いされている方もいらっしゃるため,注意が必要です。
ケプストラムが表すモノ
結局スペクトラムは何を表すの?
スペクトラムは,ほとんどの場合その低次元部分が利用されます。この低次元部分は,スペクトラムのおおまかな構造を表しているため,「スペクトル包絡」と呼ばれることもあります。つまり,周波数帯の情報を「波形」と捉えて,その低周波数部分のみを抽出することで,波形の大まかな構造を捉えようというのがケプストラムのモチベーションです。
周波数領域のおおかな構造は,人それぞれの特性を表すとされています。ですので,音声認識ではケプストラムから抽出された特徴量というのは非常に重要な役割を果たします。
実装
必要なライブラリのインポート
import librosa
import numpy as np
import matplotlib.pyplot as pltwavファイルの読み込み
# [path_to_wavfile]にはみなさんの環境に合わせたパスを入れてください
y, sr = librosa.load("[path_to_wavfile]")
plt.plot(np.arange(y.shape[0]), y)
plt.xlim(200, 1500)
plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False)
plt.tick_params(bottom=False, left=False, right=False, top=False)
plt.xlabel("Time [s]")
plt.rcParams["font.size"] = 14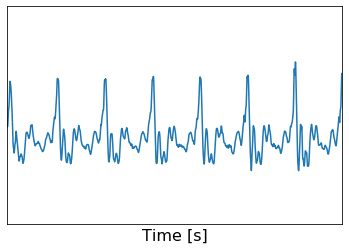
高速フーリエ変換
n = 2048
# フーリエ変換 + 振幅取得 + 対数変換
spectrum_amp_log = np.log(np.abs(np.fft.fft(y, n)))
plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False)
plt.tick_params(bottom=False, left=False, right=False, top=False)
plt.xlabel("Frequency [Hz]")
plt.rcParams["font.size"] = 14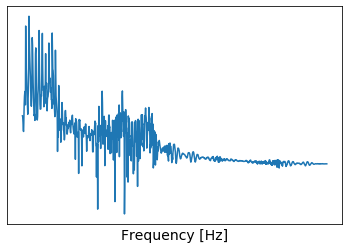
さらに高速フーリエ変換
cep = np.fft.fft(spectrum_amp_log)
plt.plot(x_axis[0:n//2], np.real(cep[0:n//2]))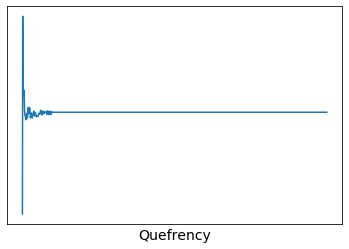
低次元のみを取り出してスペクトル包絡抽出
dims = 100
# 今までは半分までしかが層に表示していなかったことに注意
# 逆変換には左右対称部分も突っ込まなければ辻褄が合わない
# 低次元を削るということは,それに対応する高次元部も左右対称に削らなければならない
cep[dims:cep.shape[0]-dims] = 0
plt.plot(x_axis[0:n//2], log_spectrum_amp[0:n//2])
plt.plot(x_axis[0:n//2],np.real(icep[:n//2]))
plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False)
plt.tick_params(bottom=False, left=False, right=False, top=False)
plt.xlabel("Frequency [Hz]")
plt.rcParams["font.size"] = 14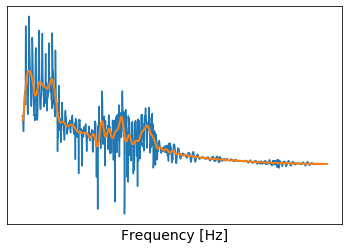
ここでは,いままでフーリエ変換の結果のうち前半部分だけを可視化していたということに注意しましょう。逆フーリエ変換の入力には,左右対称のスペクトラムを突っ込まなければならないため,低次元部分を削ると同時に,それに対応する左右対称の高次元部分も削らなければなりません。(私はここでハマりました)


















初めまして、1つ質問がありコメント失礼します。
ケフレンシーグラフは左右対称型ですが、スぺクトル包絡を抽出したグラフも左右対称型になりますでしょうか?
ご確認頂ければ幸いです。
みなさま
ご質問ありがとうございます。
当方,卒業からだいぶ年が経ってしまい,即答できないというのが正直なところです。
お力になれずすみません。
実際に適当な信号に対して実験してみると,帰納的に結論が導かれるかもしれません。