【超初心者向け】pythonで音声認識⑨「多次元正規分布の最尤推定による母音認識をしてみよう」

今回は，基本的な音声認識をpythonで行う方法をお伝えしていこうと思います。本記事はpython実践講座シリーズの内容になります。その他の記事は，こちらの「Python入門講座/実践講座まとめ」をご覧ください。

【超初心者向け】python入門講座/実践講座まとめ目次 入門講座 １．実行環境２．文字の出力３．データ型４．変数５．更新と変換６．比較演算子７．論理演算子８．条件分岐９．リスト１０．辞...

お題

流れ

今回対象とするデータは，私が喋った「あいうえお」とします。音声データを貼り付けるのは，どこか恥ずかしさを覚えるため，代わりにスペクトログラムをお見せしておきます。しっかり「あ/い/う/え/お」の発音区間が見え，最後には長い無声区間も含まれていることが分かります。

母音認識のしくみ

今回は，多次元正規分布の最尤推定に基づいて母音認識を行ってみましょう。

本シリーズ中でも，「多次元正規分布の最尤推定」は難しそうな雰囲気を醸し出している記事なのではないでしょうか。しかし，ビビる必要はありません。やっていることは単純で，「母音が生成される背後に正規分布という確率モデルを仮定して，尤（もっと）もらしい母音を解析的に求める」ということだけです。

今回は，音声を表す特徴量としてケプストラムを利用します。

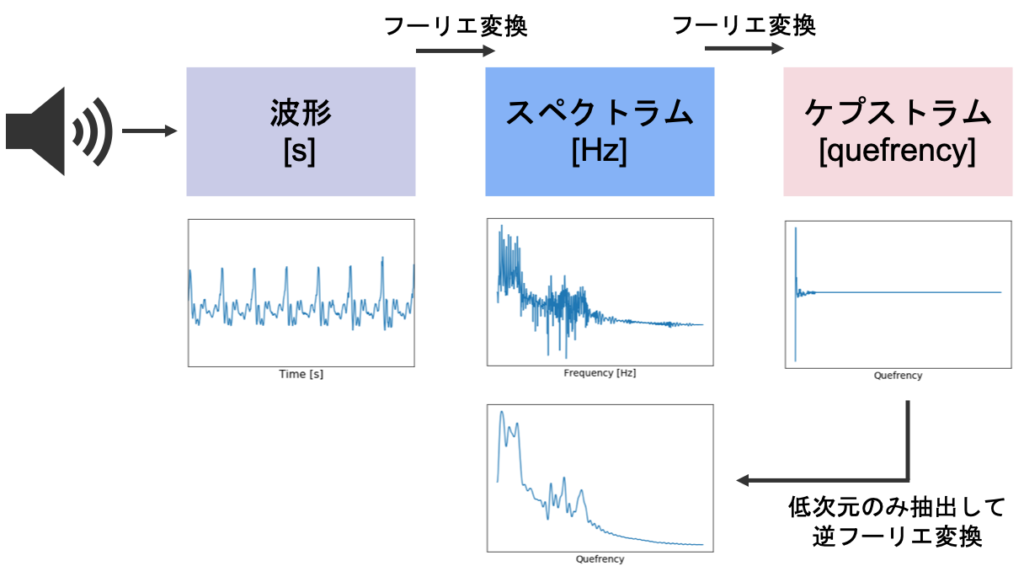
ケプストラムに関しては，以下の記事をご覧ください。

【超初心者向け】pythonで音声認識⑦「ケプストラムを抽出してみよう」 pythonで簡単な音声認識をやってみたいぞ。 そもそも何から始めればいいのかしら。 今回は，基本的な音声...

各母音のケプストラムが多次元正規分布から生成されるという仮定のもとで，計算を行っていこうというのが今回の方法です。まずは，多次元正規分布の復習からです。

多次元正規分布

多次元正規分布の確率密度関数は以下の通りです。

\begin{align}
f(\boldsymbol{x} ; \boldsymbol{\mu}, \Sigma)=\frac{1}{(2 \pi)^{D / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{(\boldsymbol{x}-\boldsymbol{\mu})^{T} \Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})}{2}\right)
\end{align}

ただし，$\boldsymbol{x}\in{\mathbb R}^{D\times N}$はある母音のフレームごとに切り出されたケプストラム集合，$\boldsymbol{\mu}\in{\mathbb R}^{D}$を多次元正規分布の平均，$\Sigma\in{\mathbb R}^{D\times D}$を共分散行列とします。ここでは，フレームごとにケプストラムは相関を持たないものとし，共分散行列を以下のような対角行列を仮定しましょう。

\begin{align}
\Sigma = \left( \begin{array}{cccc} \sigma_{1}^{2} & 0 & \ldots & 0 \\ 0 & \sigma_{2}^{2} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \sigma_{D}^{2} \end{array} \right)
\end{align}

この仮定を利用して，多次元正規分布の式を成分ごとに書き直してみます。

\begin{align}
f(\boldsymbol{x} ; \boldsymbol{\mu}, \Sigma)=\frac{1}{(2 \pi)^{D / 2} \prod_{d=1}^{D} \sigma_{d}} \exp \left(-\sum_{d=1}^{D} \frac{\left(x_{d}-\mu_{d}\right)^{2}}{2 \sigma_{d}^{2}}\right)
\end{align}

ここまでが，多次元正規分布の復習でした。

最尤推定

多次元正規分布に基づく最尤推定とは何なのでしょうか。最尤推定とは，尤度関数が最大になるようなパラメータを推定する手法のことを指します。以下の記事ではMAP推定との比較を行っています。

【これなら分かる！】変分ベイズ詳解＆Python実装。最尤推定/MAP推定との比較まで。 本記事の内容は新ブログに移行されました。 新しい記事へ こちらのブログにコメントをいただいてもご返信が遅れてしまう...

多次元正規分布の最尤推定とは，各母音ごとに対数尤度が最大になる多次元正規分布の$\boldsymbol{\mu}$と$\Sigma$ を推定するという操作に相当します。それでは，実際に計算していきましょう。多次元正規分布の対数尤度は，以下のように表されます。

\begin{align}
L &= \log p(X | \boldsymbol{\mu}, \Sigma) \\
&=\log \prod_{n=1}^{N} f \left(\boldsymbol{x}_{n} ; \boldsymbol{\mu}, \Sigma\right) \\
&=-\sum_{n=1}^{N}\left(\frac{D}{2} \log 2 \pi+\sum_{d=1}^{D} \log \sigma_{d}+\sum_{d=1}^{D} \frac{\left(x_{d, n}-\mu_{d}\right)^{2}}{2 \sigma_{d}^{2}}\right) \\
& \propto-\sum_{n=1}^{N} \sum_{d=1}^{D}\left(\log \sigma_{d}+\frac{\left(x_{d, n}-\mu_{d}\right)^{2}}{2 \sigma_{d}^{2}}\right)
\end{align}

最終行では，パラメータに関係ない定数$\frac{D}{2} \log 2 \pi$を除外しました。$-\log \sigma_{d}-\frac{\left(x_{d, n}-\mu_{d}\right)^{2}}{2 \sigma_{d}^{2}}$は$\mu_{d}$にとっても$\sigma_{d}$にとっても下に凸な関数であるため，簡単な偏微分の計算で解析的に最尤解を求めることができます。

\begin{align}
\hat{\mu}_{d} &= \frac{1}{N} \sum_{n=1}^{N} x_{n, d} \\
\hat{\sigma}_{d}^{2} &= \frac{1}{N} \sum_{n=1}^{N}\left(x_{n, d}-\mu_{d}\right)^{2}
\end{align}

この式の意味は，つまり，ある母音だけの音声データを短時間のフレームで区切って抽出したときに，各区間で計算されたケプストラムの「標本平均」と「標本分散」が多次元正規分布のパラメータの最尤解だということを示しています。

実際の母音認識では，各母音ごとに多次元正規分布のパラメータである「平均」「分散」の最尤解をもとめ，それぞれが生成される尤もらしい確率モデルができあがります。それらの生成モデルに基づいて，母音が次々と再生されるデータを短時間フレームごとに区切って，それぞれに対して得られるケプストラムの対数尤度が一番高い母音を推定結果として出力します。

だらだらと説明するより，実装をみた方が早いと思いますので，早速次に進みたいと思います。

実装

音声の読み込み

import librosa
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

y_a, sr_a = librosa.load("a.wav")
y_i, sr_i = librosa.load("i.wav")
y_u, sr_u = librosa.load("u.wav")
y_e, sr_e = librosa.load("e.wav")
y_o, sr_o = librosa.load("o.wav")

スペクトログラムの確認

plt.figure(figsize=(10, 20))

plt.subplot(5,1,1)
spec_a = librosa.stft(y_a, hop_length=int(sr_a/100), n_fft=int((sr_a/100)*4))
logmel_db_a = librosa.feature.melspectrogram(sr=sr_a, S=librosa.power_to_db(np.abs(spec_a)**2), n_mels=80)
plt.imshow(logmel_db_a, vmin=np.min(logmel_db_a), vmax=np.max(logmel_db_a), cmap="gist_heat", aspect= "auto", origin="lower")
plt.ylabel("Frequency [Hz]")
plt.title("a")

plt.subplot(5,1,2)
spec_i = librosa.stft(y_i, hop_length=int(sr_i/100), n_fft=int((sr_i/100)*4))
logmel_db_i = librosa.feature.melspectrogram(sr=sr_i, S=librosa.power_to_db(np.abs(spec_i)**2), n_mels=80)
plt.imshow(logmel_db_i, vmin=np.min(logmel_db_i), vmax=np.max(logmel_db_i), cmap="gist_heat", aspect= "auto", origin="lower")
plt.ylabel("Frequency [Hz]")
plt.title("i")

plt.subplot(5,1,3)
spec_u = librosa.stft(y_u, hop_length=int(sr_u/100), n_fft=int((sr_u/100)*4))
logmel_db_u = librosa.feature.melspectrogram(sr=sr_u, S=librosa.power_to_db(np.abs(spec_u)**2), n_mels=80)
plt.imshow(logmel_db_u, vmin=np.min(logmel_db_u), vmax=np.max(logmel_db_u), cmap="gist_heat", aspect= "auto", origin="lower")
plt.ylabel("Frequency [Hz]")
plt.title("u")

plt.subplot(5,1,4)
spec_e = librosa.stft(y_e, hop_length=int(sr_e/100), n_fft=int((sr_e/100)*4))
logmel_db_e = librosa.feature.melspectrogram(sr=sr_e, S=librosa.power_to_db(np.abs(spec_e)**2), n_mels=80)
plt.imshow(logmel_db_e, vmin=np.min(logmel_db_e), vmax=np.max(logmel_db_e), cmap="gist_heat", aspect= "auto", origin="lower")
plt.ylabel("Frequency [Hz]")
plt.title("e")

plt.subplot(5,1,5)
spec_o = librosa.stft(y_o, hop_length=int(sr_o/100), n_fft=int((sr_o/100)*4))
logmel_db_o = librosa.feature.melspectrogram(sr=sr_o, S=librosa.power_to_db(np.abs(spec_o)**2), n_mels=80)
plt.imshow(logmel_db_o, vmin=np.min(logmel_db_o), vmax=np.max(logmel_db_o), cmap="gist_heat", aspect= "auto", origin="lower")
plt.xlabel("Time_frame")
plt.ylabel("Frequency [Hz]")
plt.title("o")

それぞれ，しっかりと異なる特徴をもつスペクトログラムとなっていることが分かります。ただ，スペクトログラムでは少し特徴量として情報量が多すぎるため，ケプストラムという特徴量を利用しましょう。まずは，対数スペクトラムの計算・可視化からです。

対数スペクトラムの計算・可視化

n = 2048

# 対数スペクトラムの計算
log_spectrum_amp_a = np.log(np.abs(np.fft.fft(y_a, n)))
log_spectrum_amp_i = np.log(np.abs(np.fft.fft(y_i, n)))
log_spectrum_amp_u = np.log(np.abs(np.fft.fft(y_u, n)))
log_spectrum_amp_e = np.log(np.abs(np.fft.fft(y_e, n)))
log_spectrum_amp_o = np.log(np.abs(np.fft.fft(y_o, n)))

# 周波数軸の生成
x_axis = np.fft.fftfreq(n, (1/sr_a))
# カラーマップの指定
cm = plt.get_cmap("Set2")

# フーリエ変換の結果は左右対称なので左半分のみを可視化
plt.plot(x_axis[0:n//2], log_spectrum_amp_a[0:n//2], color=cm(0), label="a")
plt.plot(x_axis[0:n//2], log_spectrum_amp_i[0:n//2], color=cm(1), label="i")
plt.plot(x_axis[0:n//2], log_spectrum_amp_u[0:n//2], color=cm(2), label="u")
plt.plot(x_axis[0:n//2], log_spectrum_amp_e[0:n//2], color=cm(3), label="e")
plt.plot(x_axis[0:n//2], log_spectrum_amp_o[0:n//2], color=cm(4), label="o")
plt.legend()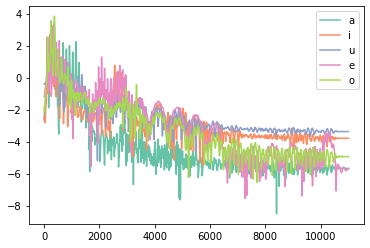

ケプストラムの計算・可視化

# 周波数領域から再びフーリエ変換を施す
cep_a = np.fft.fft(log_spectrum_amp_a, n)
cep_i = np.fft.fft(log_spectrum_amp_i, n)
cep_u = np.fft.fft(log_spectrum_amp_u, n)
cep_e = np.fft.fft(log_spectrum_amp_e, n)
cep_o = np.fft.fft(log_spectrum_amp_o, n)

# 横軸は適当に
x_axis = np.arange(cep_a.shape[0])

plt.plot(x_axis[0:n//2], np.real(cep_a[0:n//2]), color=cm(0), label="a")
plt.plot(x_axis[0:n//2], np.real(cep_i[0:n//2]), color=cm(1), label="i")
plt.plot(x_axis[0:n//2], np.real(cep_u[0:n//2]), color=cm(2), label="u")
plt.plot(x_axis[0:n//2], np.real(cep_e[0:n//2]), color=cm(3), label="e")
plt.plot(x_axis[0:n//2], np.real(cep_o[0:n//2]), color=cm(4), label="o")
plt.legend()

ケプストラムを低次元部分のみを周波数領域で可視化

# スペクトル包絡に利用する次元数
dims = 20

cep_a[dims:cep_a.shape[0]-dims] = 0
cep_i[dims:cep_i.shape[0]-dims] = 0
cep_u[dims:cep_u.shape[0]-dims] = 0
cep_e[dims:cep_e.shape[0]-dims] = 0
cep_o[dims:cep_o.shape[0]-dims] = 0

icep_real_a = np.real(np.fft.ifft(cep_a))
icep_real_i = np.real(np.fft.ifft(cep_i))
icep_real_u = np.real(np.fft.ifft(cep_u))
icep_real_e = np.real(np.fft.ifft(cep_e))
icep_real_o = np.real(np.fft.ifft(cep_o))

x_axis = np.fft.fftfreq(n, (1/sr_a))

plt.plot(x_axis[0:n//2], icep_real_a[0:n//2], color=cm(0), label="a")
plt.plot(x_axis[0:n//2], icep_real_i[0:n//2], color=cm(1), label="i")
plt.plot(x_axis[0:n//2], icep_real_u[0:n//2], color=cm(2), label="u")
plt.plot(x_axis[0:n//2], icep_real_e[0:n//2], color=cm(3), label="e")
plt.plot(x_axis[0:n//2], icep_real_o[0:n//2], color=cm(4), label="o")
plt.legend()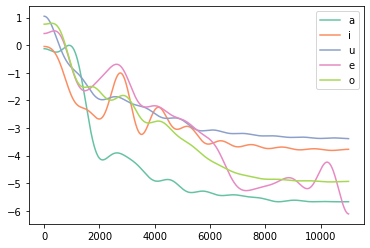

各母音の最尤推定

def calc_likelihood(X, Mu, Sigma):
  '''
  x:ケプストラム係数 (D)
  mu:ある母音のmu (D)
  sigma:ある母音のsigma (D)
  '''
  eps = 1e-8
  results = 0
  for i in range(X.shape[0]):
    results += -(np.log(np.sqrt(Sigma[i]) + eps) + (X[i] - Mu[i])**2/(2*Sigma[i] + eps))
  return results

hop_length = 512
nms = (y_a.shape[0]-2048)//hop_length

# 「あ」のケプストラム計算
cep_list_a = []
for j in range(nms):
  y_this = y_a[j*512:j*512+2048]
  log_spectrum_amp = np.log(np.abs(np.fft.fft(y_this, n)))
  cep = np.real(np.fft.fft(log_spectrum_amp))
  cep_list_a.append(cep)

# 「い」のケプストラム計算
cep_list_i = []
for j in range(nms):
  y_this = y_i[j*512:j*512+2048]
  log_spectrum_amp = np.log(np.abs(np.fft.fft(y_this, n)))
  cep = np.real(np.fft.fft(log_spectrum_amp))
  cep_list_i.append(cep)

# 「う」のケプストラム計算
cep_list_u = []
for j in range(nms):
  y_this = y_u[j*512:j*512+2048]
  log_spectrum_amp = np.log(np.abs(np.fft.fft(y_this, n)))
  cep = np.real(np.fft.fft(log_spectrum_amp))
  cep_list_u.append(cep)

# 「え」のケプストラム計算
cep_list_e = []
for j in range(nms):
  y_this = y_e[j*512:j*512+2048]
  log_spectrum_amp = np.log(np.abs(np.fft.fft(y_this, n)))
  cep = np.real(np.fft.fft(log_spectrum_amp))
  cep_list_e.append(cep)

# 「お」のケプストラム計算
cep_list_o = []
for j in range(nms):
  y_this = y_o[j*512:j*512+2048]
  log_spectrum_amp = np.log(np.abs(np.fft.fft(y_this, n)))
  cep = np.real(np.fft.fft(log_spectrum_amp))
  cep_list_o.append(cep)

# 最尤推定の計算
mu_a = np.mean(np.array(cep_list_a), axis=0)
mu_i = np.mean(np.array(cep_list_i), axis=0)
mu_u = np.mean(np.array(cep_list_u), axis=0)
mu_e = np.mean(np.array(cep_list_e), axis=0)
mu_o = np.mean(np.array(cep_list_o), axis=0)

sigma_a = np.mean((np.array(cep_list_a) - mu_a[None,:])**2, axis=0)
sigma_i = np.mean((np.array(cep_list_i) - mu_i[None,:])**2, axis=0)
sigma_u = np.mean((np.array(cep_list_u) - mu_u[None,:])**2, axis=0)
sigma_e = np.mean((np.array(cep_list_e) - mu_e[None,:])**2, axis=0)
sigma_o = np.mean((np.array(cep_list_o) - mu_o[None,:])**2, axis=0)

「あいうえお」ファイルの母音推定

ここでは，前回の記事でお伝えしたゼロ交差数による無音区間の判定も合わせて行ってみましょう。目標とする出力は，以下の通りに設定しましょう。

# 使用するファイル
y, sr = librosa.load("aiueo.wav")

# 窓をスライドさせる幅
hop_length = 512
# 窓をかける回数
nms = ((y.shape[0])//hop_length)+1

# 端にも窓をかけられるようにゼロパディング
y_bf = np.zeros(hop_length*2)
y_af = np.zeros(hop_length*2)
y_concat = np.concatenate([y_bf, y, y_af])

# 母音の推定インデックスの格納場所
pred = []
# ゼロ交差数の格納場所
zero_cross_list = []

for j in range(nms):
  zero_cross = 0
  # フレームに切り出された音声データ
  y_this = y_concat[j*512:j*512+2048]
  log_spectrum_amp = np.log(np.abs(np.fft.fft(y_this, n)))
  cep = np.real(np.fft.fft(log_spectrum_amp))
  # 対数尤度の計算
  likelihood_a = calc_likelihood(cep, mu_a, sigma_a)
  likelihood_i = calc_likelihood(cep, mu_i, sigma_i)
  likelihood_u = calc_likelihood(cep, mu_u, sigma_u)
  likelihood_e = calc_likelihood(cep, mu_e, sigma_e)
  likelihood_o = calc_likelihood(cep, mu_o, sigma_o)
  likelihood_list = [likelihood_a, likelihood_i, likelihood_u, likelihood_e, likelihood_o]
  pred.append(likelihood_list.index(max(likelihood_list)))
  # ゼロ交差数の計算
  for i in range(y_this.shape[0]-1):
    if (np.sign(y_this[i]) - np.sign(y_this[i+1]))!=0:
      zero_cross += 1
  zero_cross_list.append(zero_cross)

# 1から始まるようにインデックス修正
pred = np.array(pred) + 1

# ゼロ交差数の正規化と閾値処理
zero_cross_list = np.array(zero_cross_list)
zero_cross_list = np.array(zero_cross_list)/max(zero_cross_list)
zero_cross_list = (zero_cross_list<0.4)*1

# 以下は推定結果のスムージング
####################
for i in range(zero_cross_list.shape[0]):
  if zero_cross_list[i] == 0:
    pred[i] = 0

for i in range(pred.shape[0]-2):
  if pred[i] == pred[i+2]:
    pred[i+1] = pred[i]

# 端点の処理
if pred[-2]!=pred[-1]:
  pred[-1] = pred[-2]

for i in range(pred.shape[0]-10):
  if pred[i] == pred[i+10]:
    pred[i+5] = pred[i]

for i in range(pred.shape[0]-4):
  if pred[i]!=pred[i+1] and pred[i+1]==pred[i+2] and pred[i+2]==pred[i+3] and pred[i+3]!=pred[i+4]:
    pred[i+1]=pred[i]

for i in range(pred.shape[0]-3):
  if pred[i]!=pred[i+1] and pred[i+1]==pred[i+2] and pred[i+2]!=pred[i+3]:
    pred[i+1]=pred[i]

for i in range(pred.shape[0]-2):
  if pred[i]!=pred[i+1] and pred[i+1]!=pred[i+2]:
    pred[i+1]=pred[i]
####################

# スペクトログラムと重ねて表示
spec = librosa.stft(y, hop_length=512, n_fft=2048)
logmel_db = librosa.feature.melspectrogram(sr=sr, S=librosa.power_to_db(np.abs(spec)**2), n_mels=80)
plt.imshow(logmel_db, vmin=np.min(logmel_db), vmax=np.max(logmel_db), cmap="gist_heat", aspect= "auto", origin="lower")
plt.plot(np.arange(logmel_db.shape[1]), (pred)*10, linewidth=3.0)
plt.plot(np.arange(logmel_db.shape[1]), (zero_cross_list)*5, color="g", linewidth=3.0)
plt.xlabel("Time_frame")
plt.ylabel("Frequency [Hz]")

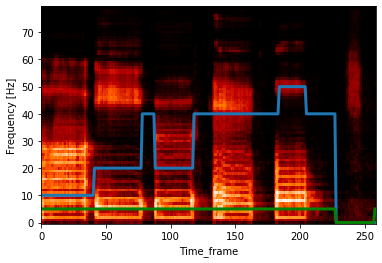
緑色が「有声 or 無声」で，線の位置が高い区間は有声と判断されています。「あ/い/う/え/お」の間の無音区間は正しく推定できていませんが，末尾の長い無音区間は正しく推定できていることが分かります。

青色が，母音の認識結果になっています。低い位置から「あ→い→う→え→お」を表しています。ファイル自体も「あ→い→う→え→お」の順番で喋っていますので，徐々に位置が高くなっていくような推定結果が正解です。ただし，無音区間は0を出力するようにしています。

上の結果を見ると，「い」と「う」の判別ができていないことが読み取れます。また，「え」が雑音（無音区間）と勘違いされてしまっています。これは，私が録音した「え」が雑音に近いような発音をしていたためだと考えられます。もしくは，もともと日本語の「え」には雑音のような響が混じっているとも考えられます。

以上をまとめると，以下のようになります。