本シリーズでは,ディープラーニングを実装する際に強力な手助けをしてくれる「PyTorch」についてです。公式チュートリアルを,初心者に向けてかみ砕きながら翻訳していこうと思います。(公式ページはこちらより)
今回はNo.3で,「ニューラルネットワーク」編です。その他の記事は,こちらの「PyTorchの公式チュートリアルを初心者向けに読み解く」をご覧ください。
全体像
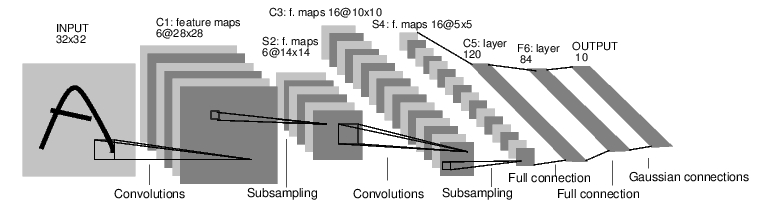 出典:https://pytorch.org/tutorials/beginner/blitz/neural_networks_tutorial.html#sphx-glr-beginner-blitz-neural-networks-tutorial-py
出典:https://pytorch.org/tutorials/beginner/blitz/neural_networks_tutorial.html#sphx-glr-beginner-blitz-neural-networks-tutorial-py上の図が,今回実装するネットワークの全体像です。最初に(32×32)の2次元のインプットを与え,(5×5)の窓で6チャネルの畳み込み層に通します。その結果,出力は(6×28×28)のテンソルになります。(正確には,0番目にサンプル数が入ります)
続いて,(6×28×28)のテンソルは(2×2)の窓でプーリングされ,出力は(6×14×14)のテンソルになります。さらに,(6×14×14)のテンソルは畳み込み層に通され,先ほどと同じ原理で(6×10×10)のテンソルとなります。同様に,プーリングされることで(6×5×5)のテンソルとなります。
(6×5×5)のテンソルは,正確には(サンプル数×6×5×5)となっています。そこで,特徴量に関係する部分を一次元配列として表す関数「num_flat_features」に通されます。あとは,一次元配列を全結合層のネットワークに通していきます。ユニット数は順に,「120→84→10」となります。結果として,(32×32)の画像は長さ10の特徴量に変換されました。
実装
必要なライブラリのインポート
import torch
import torch.nn as nn
import torch.nn.functional as F
ネットワークの定義
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:]
num_features = 1
for s in size:
num_features *= s
return num_features初学者の方々は,おそらくここで躓きやすいのではないでしょうか。まず,
となるのではないでしょうか。クラスに関して熟知されている方は問題ないかと思われますが,「とりあえずPyTorch使ってDeep実装してみよっ」という方には少々難解ですよね。クラスに関しては,以下の記事をご覧ください。

上の記事にもあるように,クラスは設計図です。つまり,上の実装ではネットワークの設計図を定義しているのです。そして,設計図の要素は「__init__」「forward」「num_flat_features」の3つのメソッドで構成されています。特に,__init__はクラス内共通のメソッドで「コンストラクタ」と呼ばれています。慣習として,(チャネル数を決定する)パラメータを持つ層を定義するのが__init__だとされています。
そして,単なる計算はforwardで定義されます。具体的には,プーリング層はチャネル数を保ったまま「縦×横」の次元を圧縮する効果を持ちますので,forwardで定義されます。
「num_flat_features」は,簡単に言えばサンプル数方向以外の特徴量に関する部分を一次元化する関数です。これは,畳み込み層(二次元)から全結合層(一次元)へと接続する部分で必要になります。
ネットワークの学習方法
一般的に,ニューラルネットワークは以下のようにして学習をしていきます。
1.ニューラルネットワークの定義
2.入力データセットの反復
3.入力をネットワークを通して処理
4.損失を計算
5.勾配の逆伝播
6.パラメータ更新(典型的な更新ルールは以下) :
weight = weight – learning_rate * gradient
ニューラルネットワークは上で定義したので,実際に呼び出してみましょう。
net = Net()
print(net)out:
Net(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=400, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)上で定義したネットワークがしっかりと反映されていますね。strideは窓のずらし幅,biasは線型結合の定数項です。いずれも,デフォルト値のままです。
学習可能なパラメータ
params = list(net.parameters())
print(len(params))
print(params[0].size())out:
10
torch.Size([6, 1, 5, 5])出力は10ユニットでしたので,パラメータの数は10になります。
具体例
入力を(32×32)と仮定して。定義したニューラルネットワークに通してみましょう。入力も4次元で与えるので,(32×32)を(1×1×32×32)に拡張してつっこみます。
input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)out:
tensor([[ 0.0431, -0.0473, 0.0501, 0.1484, -0.0412, 0.1020, 0.1341, 0.0168,
0.0231, 0.0775]], grad_fn=<AddmmBackward>)しっかりと,10個の出力が得られましたね。
バックプロップの実行
net.zero_grad()
out.backward(torch.randn(1, 10))1行目では,勾配を0で初期化しています。2行目では,出力の長さ分の重みパラメータを指定してバックプロップを実行しています。
損失関数の計算
まずは,簡単な例から考えてみたいと思います。損失関数とは,ネットワークを通して得られた出力(上の場合は10個)の値がターゲット(教師データ)とどれだけ離れているかを示す定量的な指標です。
output = net(input)
target = torch.randn(10) # 例えばのターゲット
target = target.view(1, -1) # outputと形をそろえる
criterion = nn.MSELoss()
loss = criterion(output, target)
print(loss)tensor(0.6420, grad_fn=<MseLossBackward>)上のような流れで,平均以上誤差(MSELoss)を計算することができます。バックプロップの流れは,以下のようになります。
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
-> view -> linear -> relu -> linear -> relu -> linear
-> MSELoss
-> lossためしに,「loss.grad_fn」とその前に繋がっている2つの層を確認してみましょう。
print(loss.grad_fn) # MSELoss
print(loss.grad_fn.next_functions[0][0]) # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0]) # ReLU<MseLossBackward object at 0x7fcc9b09d278>
<AddmmBackward object at 0x7fcc9b09d0b8>
<AccumulateGrad object at 0x7fcc9b09d278>
実際に,勾配を0で初期化してからloss.backward()でバックプロップしてみましょう。
net.zero_grad()
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)out:
conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([-8.4137e-05, -1.2695e-02, 2.7627e-03, 4.4243e-03, 8.6504e-04,
7.2595e-03]).backward()を実行する前はたしかに0で初期化されており,実行後はしっかりと計算されていることが分かります。
重みの更新
単純な勾配法は,以下のようにして実装できます。
learning_rate = 0.01
for f in net.parameters():
f.data.sub_(f.grad.data * learning_rate)1行目では,学習率を設定しています。2行目以降では,学習した全てのパラメータに関して勾配法の式を用いて重みを更新しています。
しかし,PyTorchにはもっと便利なパッケージが定義されています。
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.01)
optimizer.zero_grad()
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()1行目で様々な最適化手法を含むoptimをインポートしています。今回は,SGD(確率的勾配降下法)を指定しています。そのあとは,基本的に同じ流れです。0で勾配を初期化したのちに,inputをネットワークに通してoutputを得ます。lossは先ほど定義した平均二乗誤差で測り,計算されたlossを元にバックワードを実行します。そして,最後に重みパラメータの更新を行います。



















