今回は，Pythonをパズルに利用する方法をお伝えしていこうと思います。パズルを題材にした練習は，自分でデータ構造を定義してアルゴリズムを考えていかなくてはならないため，非常によい練習になります。
本記事はpython実践講座シリーズの内容になります。その他の記事は，こちらの「Python入門講座/実践講座まとめ」をご覧ください。
読みたい場所へジャンプ！
実装
こちらのURLよりGitHubページにアクセスしてください。
パズルの概要
シャッフルされた擬似EternityEternityIIは，難解パズルの１つです。2008年に発売され，懸賞金約２億円が懸けられましたが，いまだに誰も解くことができていません。ちなみに，懸賞金は2010年に終了しています。上の図では３×３になっていますが，ホンモノは16×16の大きさです。
パズルのルールは簡単で，外側は黒色，内側は隣り合うピースが同じ色になるように敷き詰めていきます。
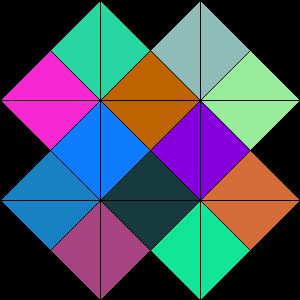3×3の擬似Eternity
と感じますよね。でも，考えてみてください。世界の天才科学者たちが約10年間頭を悩ませても解くことができていないパズルなのです。そこで，今回考えるパズルはホンモノを少し簡単にします。「擬似EternityII」という言い方をしています。以下に，擬似EternityIIの特徴を挙げておきます。
【擬似EternityIIの特徴】
①パズルのサイズは可変
②内側の色の種類も可変
③ピースは回転しない
④真ん中のピースは元から埋まっている
⑤１辺のサイズは奇数
まず大前提として，擬似EternityIIは自分でパズルを作成することから始めます。ですので，パズルの大きさや外側の黒以外に使う色の種類は自分で決められます。
ピースが回転しないことで，ホンモノのEternityIIよりもかなり簡単になっています。また，ホンモノのEternityIIでも真ん中のピースは元から埋まっていますが，16×16のサイズですのでそれは「ど真ん中」のピースではないのです。パズル作成の観点から，辺の数を奇数個に限定することで，ど真ん中のピースが元から埋まっているようにしておきます。
人間が解く分には簡単そうなのですが，プログラムにやらせると意外とやっかいなのです。それでは早速，Python上でパズルを定義していきましょう。
データ構造の定義
パズルのピースは，配列構造で表すことにします。また，色の種類を整数で表します。特に，黒色は特徴的なので「0」と定義します。また，配列のインデックスと色の配置を以下のように定めます。
[左， 上， 右， 下]たとえば，このピースは以下のように表されます。
[0,0,3,6]この配列を使うことでパズルを表し，「隣り合うピースが同じ色になるように」並び替えていくことが目標です。
アルゴリズムの流れ
まず最初に，インプットとしてパズルのサイズと色の種類を与えます。次に，それらのパラメータをもとに，擬似EternityIIを作成します。続いて，生成されたパズルを入力として自分で定義したSolverを利用します。Solverの出力は先ほど定義した配列になっているので，それを視覚化して合致率を評価していきます。ちなみに，合致率（Accuracy）は以下のように計算するとします。
\begin{eqnarray}
\rm{Accuracy} = \frac{(合っている領域)}{(全部の領域)}
\end{eqnarray}
アルゴリズムの詳細
さて，以下では実際にコードを眺めながらアルゴリズムをお伝えしていこうと思います。
必要なライブラリ等のインポート
import random
from PIL import Image, ImageDraw
import IPython
import sys
import matplotlib.pyplot as pltcolaboratory上では視覚化を上手く行う方法がまだないため，一旦画像に保存してその画像を表示するという手法を取ることにします。PILを使ってパズルを描写して，IPythonで表示します。sysは進行状況を上書きしながらprintするためにインポートしています。pltは最後の解析で，グラフを出力するときに利用します。
パズルを作る関数
def generate_puzzle(n, color):
N = n**2
inner = N*4 - n*4
same_color_nm = inner / color
field = [[0,0,0,0] for i in range(N)]
palette = [i+1 for i in range(color)]
palette = random.sample(palette, len(palette))
# 縦方向に塗っていく
count = 0
for i in range(n-1):
for j in range(n):
field[n*i+j][3] = palette[count]
field[n*i+j+n][1] = palette[count]
if count == color-1:
count = 0
palette = [i+1 for i in range(color)]
palette = random.sample(palette, len(palette))
else:
count += 1
# 横方向に塗っていく
for i in range(n):
for j in range(n-1):
field[n*i+j][2] = palette[count]
field[n*i+j+1][0] = palette[count]
if count == color-1:
count = 0
palette = [i+1 for i in range(color)]
palette = random.sample(palette, len(palette))
else:
count += 1
return fieldパズルを作る関数です。1辺と色の数を指定するだけでパズルを作成するようにしています。
指定した色数が適当かを判断する関数
def check_parameters(n, color):
N = n**2
inner = N*4 - (n*4)
if inner<color*2:
print("colorを別の値にしてください！ \nとりあえず"+str(inner//2)+"色で塗り分けます！")
else:
print("OKです！")パズル内の色を塗り分ける領域数よりも，色の数の方が多くなってしまったら警告を出すように設定しています。
四角を埋める関数
def fill_corner(X, Y, Remains):
N = len(X)
n = int(pow(N, 0.5))
X_index = list(range(N))
corner_0_index = [i for i in X_index if (X[i][0]==0 and X[i][1]==0)]
corner_0 = X[corner_0_index[0]]
corner_1_index = [i for i in X_index if (X[i][1]==0 and X[i][2]==0)]
corner_1 = X[corner_1_index[0]]
corner_2_index = [i for i in X_index if (X[i][0]==0 and X[i][3]==0)]
corner_2 = X[corner_2_index[0]]
corner_3_index = [i for i in X_index if (X[i][2]==0 and X[i][3]==0)]
corner_3 = X[corner_3_index[0]]
corner = [corner_0, corner_1, corner_2, corner_3]
for i in range(4):
Remains.remove(corner[i])
Y[0] = corner_0
Y[n-1] = corner_1
Y[N-n] = corner_2
Y[N-1] = corner_3
return Y, Remains
今回の擬似EternityIIでは，回転がないため四角が埋まってしまいます。そこで，この関数ではパズルを埋めていくフィールド（Y）に四角を入れていく操作を施します。その際，残りピースのRemainも作っておきます。
インデックスからピースの場所を出力する関数
def judge(n, index):
N = n**2
corner0 = [0]
corner1 = [n-1]
corner2 = [N-n]
corner3 = [N-1]
left = [n + i*n for i in range(n-2)]
above = [1 + i for i in range(n-2)]
right = [2*n-1 + i*n for i in range(n-2)]
below = [N-n+1 + i for i in range(n-2)]
lookup = [corner0,corner1,corner2,corner3,left, above, right, below]
element = [flatten for inner in lookup for flatten in inner]
if index < 0 or index > N:
return None
elif index in element:
for i in range(len(lookup)):
if index in lookup[i]:
return i
else:
return 8
# 0-3:corner, 4:left, 5:above, 6:right, 7:below, 8:center$n$とインデックスから，そのピースの場所を「四角，左エッジ，上エッジ，右エッジ，下エッジ，それ以外の真ん中」と９種類に分類します。こうすることで，場所ごとの操作が可能になります。
周りでinしているピース数を出力する関数
def get_around_in_nm(n, index, estimate):
if judge(n, index)==0:
count = 2
if type(estimate[index+1]) == list or estimate[index+1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+n]) == list or estimate[index+n]==[-1,-1,-1,-1]:
count += 1
return count
elif judge(n, index)==1:
count = 2
if type(estimate[index-1]) == list or estimate[index-1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+n]) == list or estimate[index+n]==[-1,-1,-1,-1]:
count += 1
return count
elif judge(n, index)==2:
count = 2
if type(estimate[index-n]) == list or estimate[index-n]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+1]) == list or estimate[index+1]==[-1,-1,-1,-1]:
count += 1
return count
elif judge(n, index)==3:
count = 2
if type(estimate[index-n]) == list or estimate[index-n]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index-1]) == list or estimate[index-1]==[-1,-1,-1,-1]:
count += 1
return count
elif judge(n, index)==4:
count = 1
if type(estimate[index-n]) == list or estimate[index-n]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+1]) == list or estimate[index+1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+n]) == list or estimate[index+n]==[-1,-1,-1,-1]:
count += 1
return count
elif judge(n, index)==5:
count = 1
if type(estimate[index-1]) == list or estimate[index-1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+1]) == list or estimate[index+1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+n]) == list or estimate[index+n]==[-1,-1,-1,-1]:
count += 1
return count
elif judge(n, index)==6:
count = 1
if type(estimate[index-n]) == list or estimate[index-n]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index-1]) == list or estimate[index-1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+n]) == list or estimate[index+n]==[-1,-1,-1,-1]:
count += 1
return count
elif judge(n, index)==7:
count = 1
if type(estimate[index-n]) == list or estimate[index-n]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index-1]) == list or estimate[index-1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+1]) == list or estimate[index+1]==[-1,-1,-1,-1]:
count += 1
return count
if judge(n, index)==8:
count = 0
if type(estimate[index-n]) == list or estimate[index-n]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index-1]) == list or estimate[index-1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+1]) == list or estimate[index+1]==[-1,-1,-1,-1]:
count += 1
if type(estimate[index+n]) == list or estimate[index+n]==[-1,-1,-1,-1]:
count += 1
return count先ほど定義したjudge関数を利用して，各場所ごとに処理を施していきます。[-1,-1,-1,-1]というのは，後ほどエラー回避のために定めたダミーピースで，まだはめられていないピースを表します。（本来であれば，フィールドを作成するときにそう定めてしまうのがベストだと思います）
周りで一致している領域の数を出力する関数
def get_around_pattern_nm(n, index, piece, estimate):
if judge(n, index) == 4:
if type(estimate[index - n]) == int:
estimate[index - n] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index + 1]) == int:
estimate[index + 1] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index + n]) == int:
estimate[index + n] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
num = set(enumerate(piece)) & set(enumerate([0,estimate[index - n][3], estimate[index + 1][0],estimate[index+n][1]]))
elif judge(n, index) == 5:
if type(estimate[index - 1]) == int:
estimate[index - 1] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index + 1]) == int:
estimate[index + 1] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index + n]) == int:
estimate[index + n] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
num = set(enumerate(piece)) & set(enumerate([estimate[index - 1][2], 0, estimate[index + 1][0],estimate[index+n][1]]))
elif judge(n, index) == 6:
if type(estimate[index - n]) == int:
estimate[index - n] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index - 1]) == int:
estimate[index - 1] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index + n]) == int:
estimate[index + n] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
num = set(enumerate(piece)) & set(enumerate([estimate[index - 1][2], estimate[index - n][3], 0, estimate[index+n][1]]))
elif judge(n, index) == 7:
if type(estimate[index - n]) == int:
estimate[index - n] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index - 1]) == int:
estimate[index - 1] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index + 1]) == int:
estimate[index + 1] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
num = set(enumerate(piece)) & set(enumerate([estimate[index - 1][2], estimate[index - n][3], estimate[index + 1][0], 0]))
elif judge(n, index) == 8:
if type(estimate[index - n]) == int:
estimate[index - n] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index - 1]) == int:
estimate[index - 1] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index + 1]) == int:
estimate[index + 1] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
if type(estimate[index + n]) == int:
estimate[index + n] = [-1,-1,-1,-1] #適当な負の数を入れることでsetで数え上げないようにしている
num = set(enumerate(piece)) & set(enumerate([estimate[index - 1][2], estimate[index - n][3], estimate[index + n][0], estimate[index + n][1]]))
return numこのアルゴリズムの肝となる部分です。リスト形式で表された各ピースをenumerate関数を使ってインデックス付与して，setで集合化することで論理演算を行なっています。もしenumerateを使わなければ色の順番がごちゃまぜでも，同じ色が使われていれば「同じ色が隣り合った」と出力されてしまうので注意です。
残りピースのインデックスを出力する関数
def calc_remain_index(Y):
index = []
for i in range(len(Y)-1):
if type(Y[i])==int or Y[i]==[-1,-1,-1,-1] :
index.append(i)
return index残りピースのインデックスを出力します。この関数がなければ，各ピースは位置情報を失ってしまいます。
パズルを視覚化する関数
def draw_puzzle(Y, name, color_code):
N = len(answer)
n = int(pow(N, 0.5))
im = Image.new('RGB', (n*100,n*100), color_code[0])
draw = ImageDraw.Draw(im)
a = 100
count = 0
for i in range(n):
for j in range(n):
draw.polygon((0+j*a,0+i*a,a//2+j*a,a//2+i*a,0+j*a,a+i*a), fill=color_code[Y[count][0]], outline=(0,0,0))
draw.polygon((0+j*a,0+i*a,a//2+j*a,a//2+i*a,a+j*a,0+i*a), fill=color_code[Y[count][1]], outline=(0,0,0))
draw.polygon((a+j*a,0+i*a,a//2+j*a,a//2+i*a,a+j*a,a+i*a), fill=color_code[Y[count][2]], outline=(0,0,0))
draw.polygon((0+j*a,a+i*a,a//2+j*a,a//2+i*a,a+j*a,a+i*a), fill=color_code[Y[count][3]], outline=(0,0,0))
count +=1
im.save(name+".png")
IPython.display.Image(name+".png")EternityIIを視覚化する試みはいまだに少なく思えます。このように視覚化していくことで，間違えの傾向や定性的な発見に繋がるのではないかと考えています。一旦画像として保存して，その画像を表示するという手法で画像を出力しています。
パズルをシャッフルする関数
def shuffle(answer):
X = random.sample(answer, len(answer))
return X単に，生成されたパズルをシャッフルする関数です。
シャッフルされたパルズを生成する関数
def puzzle_making(answer):
X = list(answer)
center_index = (N-1)//2
center = answer[center_index]
X.pop(center_index)
X = shuffle(X)
X.insert(center_index, center)
return X真ん中を埋めた状態でパズルを作成する関数です。
def data_making(X):
center_index = (N-1)//2
center = X[center_index]
Y = list(range(N))
Y[center_index] = center
Remains = list(X)
Remains.remove(center)
return Y, Remainsフィールドと残りピースを生成する関数です。
合致率を計算する関数
def check(Y):
N = len(Y)
n = int(pow(N, 0.5))
count = 0
# vertex
if Y[0][0]==0:
count +=1
if Y[0][1]==0:
count +=1
if Y[0][2]==Y[1][0]:
count +=1
if Y[0][3]==Y[n][1]:
count +=1
if Y[n-1][0]==Y[n-2][2]:
count +=1
if Y[n-1][1]==0:
count +=1
if Y[n-1][2]==0:
count +=1
if Y[n-1][3]==Y[n-1+n][1]:
count +=1
if Y[N-n][0]==0:
count +=1
if Y[N-n][1]==Y[N-n-n][3]:
count +=1
if Y[N-n][2]==Y[N-n+1][0]:
count +=1
if Y[N-n][3]==0:
count +=1
if Y[N-1][0]==Y[N-2][2]:
count +=1
if Y[N-1][1]==Y[N-1-n][3]:
count +=1
if Y[N-1][2]==0:
count +=1
if Y[N-1][3]==0:
count +=1
# edge
for i in range(n-2):
if Y[i+1][0]==Y[i][2]:
count +=1
if Y[i+1][1]==0:
count +=1
if Y[i+1][2]==Y[i+2][0]:
count +=1
if Y[i+1][3]==Y[i+1+n][1]:
count +=1
if Y[n+i*n][0]==0:
count +=1
if Y[n+i*n][1]==Y[i*n][3]:
count +=1
if Y[n+i*n][2]==Y[n+i*n+1][0]:
count +=1
if Y[n+i*n][3]==Y[n+i*n+n][1]:
count +=1
if Y[n+n-1 + n*i][0]==Y[n+n-1 + n*i -1][2]:
count +=1
if Y[n+n-1 + n*i][1]==Y[n-1 + n*i][3]:
count +=1
if Y[n+n-1 + n*i][2]==0:
count +=1
if Y[n+n-1 + n*i][3]==Y[n+n-1 + n*i +n][1]:
count +=1
if Y[N-n++1 + i][0]==Y[N-n + i][2]:
count +=1
if Y[N-n+1 + i][1]==Y[N-n+1 + i -n][3]:
count +=1
if Y[N-n+1 + i][2]==Y[N-n+1 + i+1][0]:
count +=1
if Y[N-n+1 + i][3]==0:
count +=1
# inner
for i in range(n-2):
for j in range(n-2):
if Y[i+(j+1)*n+1][0]==Y[i+(j+1)*n][2]:
count += 1
if Y[i+(j+1)*n+1][1]==Y[i+(j+1)*n+1-n][3]:
count += 1
if Y[i+(j+1)*n+1][2]==Y[i+(j+1)*n+1+1][0]:
count += 1
if Y[i+(j+1)*n+1][3]==Y[i+(j+1)*n+1+n][1]:
count += 1
return count隣り合う色が同じ色かを原始的な方法で確かめていきます。これも各領域に対して操作を施していきます。
スコアを元に埋めるインデックスを選択する関数
def index_sorting(n,estimate, remains):
score = []
piece = []
for index in calc_remain_index(estimate):
number = [0 for i in range(len(remains))]
for i in range(len(remains)):
number[i] = len(get_around_pattern_nm(n, index, remains[i], estimate))
max_index = number.index(max(number))
if (judge(n,index)==8) and (0 in remains[max_index]):
while 0 in remains[max_index]:
number.pop(max_index)
max_index = number.index(max(number))
if len(number)==1:
break
if (judge(n, index)==(4 or 5 or 6 or 7) and (0 not in remains[max_index])) == True:
while 0 not in remains[max_index]:
number.pop(max_index)
max_index = number.index(max(number))
if len(number)==1:
break
score.append(number[max_index])
piece.append(remains[max_index])
return score, pieceSolverのなかでも一番大切な関数です。隣り合う４つの領域のうち何個の色が合っているかをスコアとして受け取り，そのスコアが高いインデックス順にパズルを埋めていきます。インデックスは，フィールド上の位置を意味しています。同時に，外側のピースは黒色が含まれるように，内側は含まれないように制限をかけています。どうしてもその制限がクリアできなかった場合には，最後に参照されたピースを返すようにしています。
カラーコードを生成する関数
def generate_random_color():
r = lambda: random.randint(0,255)
code = '#%02X%02X%02X' % (r(),r(),r())
return code16進数のカラーコードを生成します。
指定した数だけ色を生成する関数
def making_color(color):
color_code = [generate_random_color() for i in range(color+1)]
color_code[0] = "#000000"
color_code[-1] = "#ffffff"
return color_codecolorで指定した分だけ色を生成します。注意点としては，0番目には外側の黒色を，color番目にはまだ埋められていないことを表す白色を格納しておきます。先ほどなにも入っていないフィールドに[-1,-1,-1,-1]を入れたのもそのためです。
パズルを解く関数
def solve(X):
Y, Remains = data_making(X)
Y, Remains = fill_corner(X, Y, Remains)
for i in range(len(Remains)):
remain_index = calc_remain_index(Y)
score,piece = index_sorting(n,Y,Remains)
max_index = score.index(max(score))
index = remain_index[max_index]
max_piece = piece[max_index]
Y[index] = max_piece
print("\r"+str(int(round((i/len(Remains)),2)*100))+"%完了", end="")
return Yついにきました。シャッフルされたパズルXを入力として受け取り，全部のピースをスコア順に埋めていったYを出力します。そのときに，上書きしながら進行状況を出力していきます。
解析を行う処理
fig, axes = plt.subplots(7, 1, figsize=(10, 20))
plt.subplots_adjust(hspace=0.6)
for i in range(2):
n = 2*(i+5) + 3
y_list = []
x_list = range(((n*n*4 - 4*n)//2) - 1)
for j in range(((n*n*4 - 4*n)//2) - 1):
color = j+2
answer = generate_puzzle(n, color)
N = len(answer)
X = puzzle_making(answer)
Y = solve(X)
score = int((check(Y)/(N*4)) * 100)
y_list.append(score)
axes[i].plot(x_list, y_list)
axes[i].set_title("Match rate")
axes[i].set_xlabel("Color")
axes[i].set_ylim([0,120])
print("\n"+str(i+1)+"回目", end="")
print("\nサイズは"+str(n))
print(y_list)
plt.show()このようなコードによって，色の種類と合致率の関係を定量評価することができます。一般に，色の数が多いほど自由度が低くなるのでパズルの難易度は簡単になります。ちなみに，ホンモノのEternityIIは16×16で色の数は外側含めて23色です。
簡単な実験
色の数が合致率にどのような影響を与えるかについて，簡単な実験を行いました。
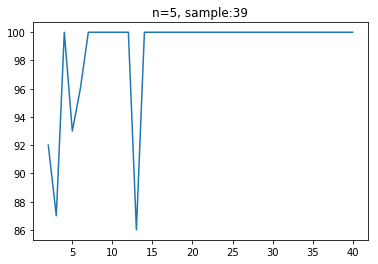
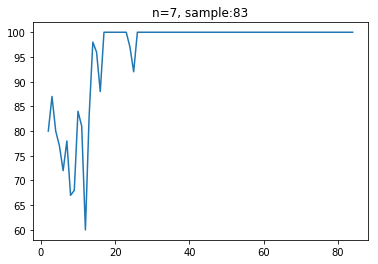
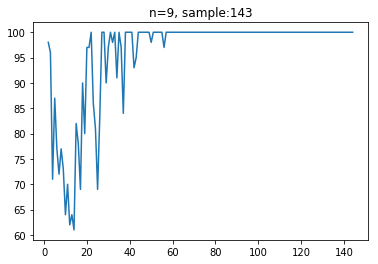
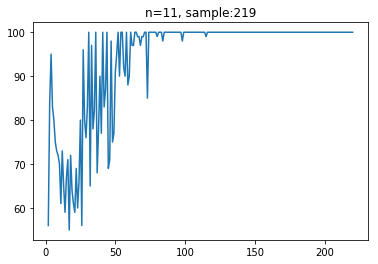
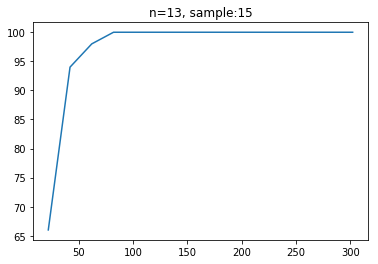
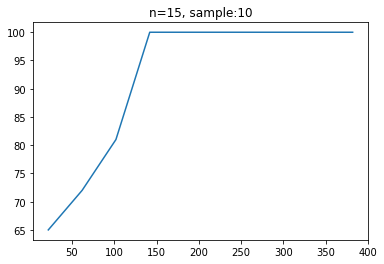
言われれば当然ですが，色の種類が増えることによってパズルの自由度が減少するため，合致率が像がする傾向にあることがわかりました。また，合致率が100%より減少する点をいくつか調べてみたところ，以下のような正解が出力されていました。
上の例では，パズルの生成過程で同じピースが出現しているため，その分自由度が増えてしまい，結果として合致率が100%を切ってしまっています。
また，下の例では，合致率は99%を達成しているものの，左下あたりに１つだけ色の異なる領域が隣り合っているピースがあります。これは，非常に稀な局所解に陥っていることを示しています。まずは，このような局所解に陥らないようなパズル生成のアルゴリズムに修正する必要がありあります。（現在は色の塗り方をパターン化しているため，完全ランダムかする）
まとめ
今回は，コーディングやアルゴリズムの練習としてEternityIIをとりあげました。ホンモノには手も足も及ばなかったため，このような形で簡易化したEternityIIを扱うことで，プログラミングでパズルを解くとはどういうことなのかを少し理解できた気がします。
