主にコンサル系の職を希望されている方であれば,必ずや通るであろう選考の一つに「ケース面接」があります。ケース面接とは,ざっくり言えばあるお題に対して「妥当な仮説を立てながら論理的に結論を導き出す」能力を測るような面接です。この記事では,主にケース面接初心者の方々に向けて,抽象的な概念に終始しない対策法をお伝えしていこうと思います。
その他の就活系の記事は,以下の目次をご覧ください。

読みたい場所へジャンプ!
この記事の出どころ
本記事は「現役東大生が書いた地頭を鍛えるフェルミ推定ノート」の内容を参考にして執筆しています。こちらの参考書は,適度なキャッチーさで非常に分かりやすいため,おすすめです。
ケース面接の分類
敵と戦うためには,まず敵を知るところから始めましょう。ケース面接の大まかな分類を把握しておくことで,体系立てて戦略を作っていくことができます。
【ケース面接の分類】
1.フェルミ推定
2.戦略策定
3.アイディア発案
フェルミ推定
出ました。言葉だけが独り歩きしていますが,ケース面接といえばフェルミ推定です。フェルミ推定は,何かしらの数や量を予測するというタスクになります。例えば「日本でラーメンは1日何皿食べられているか」というようなお題です。
フェルミ推定は大きく分類すると以下のようになります。後で,例題と照らし合わせながら解法を見ていきます。
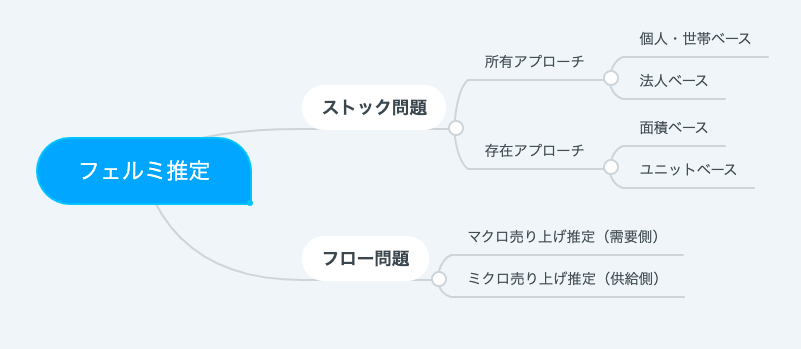
ここで求められているのは,決して正確な答えではありません。仮定を置きながら妥当な見積もりを立てられる能力が必要になります。例えば「日本人の平均1割の人口が毎日ラーメンを食べているだろう」と仮定を立てれば,単純計算で1億3000万人の1割ですから,1300万人ということになります。しかし,果たしてこの仮定は妥当でしょうか。どこに,日本人の平均1割の人口が毎日ラーメンを食べていると考えられる根拠があるのでしょうか。これらの仮定の妥当性をある程度保証しながら思考を進められるキーアイディアが「MECE」になります。下で詳しく説明します。
戦略策定
「東京のラーメン屋さんが売り上げを伸ばすためには?」というようなお題が戦略策定に分類されます。この類のタスクは,フェルミ推定が前提となっています。というのも,具体的な数値や複数の仮定を置かなければ,根拠があり説得力のある回答はできないからです。
つまり,戦略策定系のケース面接では,まずフェルミ推定を利用して対象を分析します。その上で,各セグメントに対して戦略を立てていくという流れになります。こちらも,フェルミ推定同様に正しい答えが求められているわけではなく,MECEに則った考え方がみられています。
アイディア発案
こちらの分類は,戦略策定とほぼ同義です。イメージとしては,戦略策定よりも抽象度が高くなったタスクがアイディア発案です。例えば「ラーメン屋さんで発売するべき新商品とは」などです。この類のタスクでは,まずはお題を噛み砕いて抽象度を落とす作業から始めなくてはなりません。なぜなら「発売するべき」という部分があまりにも不明瞭すぎるからです。
そこで,以下のように具体的なお題に落とし込んでしまいましょう。
「東京」で「新しく開店する」ラーメン屋さんが「夏」に「知名度を向上させるために」行うべき施策とは。
ここで意識するべきなのは「5W1H」です。もはや小学生でも知っている言葉ですが,抽象的な概念を具体に落とし込む際には非常に有用なアイディアです。そして,お察しの通りお題を噛み砕いた後はフェルミ推定が待ち受けているわけです。
MECE
うえで見てきたように,どのお題にしても「フェルミ推定」は必須の作業になります。そこで必ず求められるアイディアが「MECE(ミーシー)」と呼ばれるものです。MECEは「Mutually Exclusive and Collectively Exhaustive」の頭文字を取ったもので,「モレなく・ダブりなく」を意味しています。
一体何にMECEを適用すればいいの?
MECEは,お題に回答するために必要な「仮定の妥当性」を主張するために使われるアイディアです。そして,MECEを実現するためには,いくつかの代表的なフレームワークを利用するとかなり楽です。後で例題を通して一緒にみていきますが,一旦フレームワークの説明をしていきます。非常にたくさんのフレームワークが乱立していますが,ここでは「仮定の妥当性」を分かりやすく整理して伝えるために特に有用だと考えられるものについて紹介していきます。
因数分解
定番中の定番ですね。ある現象を複数の要素の掛け算(もしくは足し算)で表そうとするアイディアが因数分解です。「困難は分割せよ」というデカルトの名言のように,ある現象を細かな要素に分解していくことで仮定の妥当性を高めることができます。
3C分析
3C分析は自社の立ち位置を確認するために用いられるアイディアです。「顧客・市場(customer)」「競合(competitor)」「自社(company)」とすることで,より多角的な方策を練ることができます。
4P分析
4P分析は,自社と他者を比較する際に重要となる観点を示しています。「品質(Product)」「価格(Price)」「Place(立地)」「Promotion(宣伝)」の4つの観点から比較検討を行うと良いでしょう。
SWOT分析・クロスSWOT分析
戦略策定のフレームワークの中で最も有名とも言えるものが,SWOT分析です。SWOT分析では「外部・内部」「助け・妨げ」の二項対立する概念でマトリックスを作ります。
| 助け | 妨げ | |
| 外部 | Strength (強み) |
Weakness (弱み) |
| 内部 | Opportunities (機会) |
Threats (脅威) |
これらの背反な分類を使って戦略を策定しようと発展させたものがクロスSWOT分析です。
| 強み(S) | 弱み(W) | |
| 機会(O) | SO戦略 | WO戦略 |
| 脅威(T) | ST戦略 | WT戦略 |
フェルミ推定に必要な前提知識
考え方は分かったけど,そもそも仮定を置いたときに数値を知らなければ意味ないよね?
フェルミ推定では,ある程度の前提知識があるとかなり便利です。以下に有用な情報をまとめておきます。
フェルミ推定の「解き方」
さて,ここからは一般論ではなく実践的な解法をお伝えしていこうと思います。観点はフェルミ推定の分類に基づけばOKです。一般的な解法としては,以下のような流れになります。例題で一緒に見ていきます。
【フェルミ推定の解き方】
1.前提確認
2.アプローチ設定
3.モデル化
4.計算実行
5.現実性検証
例題
さて,ここからはいくつかの例題を用いてMECEに則ったケース面接の対策を立てていきましょう。
例1:日本にピアスはいくつあるか
分類としてはフェルミ推定の「ストック問題ー所有アプローチ」に該当します。実際に解法の流れに沿って解いていきましょう。
前提確認
ピアスの定義を確認します。簡単のため,ここでは日本人が「所有している」ピアスということにします。つまり,トラックで配達中のピアスや店頭で販売中のぬいぐるみは無視してしまいます。また,2個で1セットと数えます。
アプローチ設定
日本人が所有しているピアスの数は
日本の人口×ピアス平均所有率×1人あたりの平均所有数
で求められると仮定します。
モデル化
日本の人口(1億2千万人)を10歳ごとに男女のセグメントに分けます。各セグメントの平均所有率と平均所有数は以下のように仮定します。また,人口は20歳ごとに「2:3:3:2」の比率でつぼ型に分布しており,男女比は1:1と仮定します。
| 人口 | 平均所有率(女/男) | 平均所有数 | |
| 0-9 | 1200万人 | 10/0% | 1 |
| 10-19 | 1200万人 | 50/10% | 1 |
| 20-29 | 1800万人 | 80/10% | 5 |
| 30-39 | 1800万人 | 80/10% | 5 |
| 40-49 | 1800万人 | 80/10% | 5 |
| 50-59 | 1800万人 | 70/10% | 3 |
| 60- | 2400万人 | 70/10% | 3 |
計算実行
上の公式に当てはめて計算すると
1億7610万セット
となりました。
現実性検証
1億7610万セットという数字は,全ての日本人がピアスを平均1.5セット所有しているという数字です。男性がほとんど所有していないと仮定すると,女性が平均3セット所有している計算になります。少し多すぎる印象を受けますが,平均所有率と平均所有数を多く見積もりすぎていたからかもしれません。
例2:日本に猫は何匹いるか
分類としてはフェルミ推定の「ストック問題ー所有アプローチ」に該当します。先ほどの同様です。実際に解法の流れに沿って解いていきましょう。
前提確認
猫の定義を確認します。簡単のため,ここでは日本人が「所有している」猫ということにします。つまり,店頭で販売中の猫や野良猫などは無視してしまいます。
アプローチ設定
日本人が所有している猫の数は
日本の世帯数×猫平均世帯所有率×1世帯あたりの平均所有数
で求められると仮定します。
モデル化
日本の世帯数をセグメントに分けます。セグメントの分け方としては,猫を飼うか飼わないかを決めるような軸が妥当と思われます。ここでは,3人以下か4人以上で世帯平均年齢をベースに分類していきます。
(3人以下)
| 所有率 | 平均所有数 | |
| 20-29 | 20% | 1 |
| 30-39 | 20% | 1 |
| 40-49 | 30% | 1.5 |
| 50-59 | 30% | 1.5 |
| 60- | 30% | 1.5 |
(4人以上)
| 所有率 | 平均所有数 | |
| 20-29 | 10% | 2 |
| 30-39 | 10% | 2 |
| 40-49 | 20% | 2 |
| 50-59 | 20% | 2 |
| 60- | 20% | 2 |
所有率は,寂しさという観点から3人以下の家族の方が平均的に高いと考えられます。また,所有数は,大家族の方が平均的に高いと考えられます。また,3人以下の家族数と4人以上の家族数の比率は1:1とし,各世帯の平均人数はそれぞれ1.5人と5人にします。また,各年代の比率も等しいと仮定します。
計算実行
上の公式に当てはめて計算すると
1784万匹
となりました。
現実性検証
実際の世帯数が約5000万世帯ということを知っていれば,約3世帯に1世帯の割合で猫を飼っているということが分かります。少し多すぎる印象を受けますね。そこで,犬と猫を半々の割合で選ぶと仮定すれば,約900万匹という結果になり,約6世帯に1世帯の割合で猫を飼っているということになります。実際に,一般社団法人ペットフード協会によると,2018年の飼育猫数は964万9千頭ということでした。900万匹という数字はかなりいい線いっています。
例3:日本にコピー機は何台あるか
分類としてはフェルミ推定の「ストック問題」に該当します。アプローチ方法は「法人・世帯」とします。実際に解法の流れに沿って解いていきましょう。
前提確認
コピー機の定義を確認します。ここではコピー機を「public」なものと「private」なものに分類します。参考書に則って,publicは「会社」と「学校」に分けられるものとします。また,privateは世帯ベースでモデル化していくことにします。
アプローチ設定
publicなコピー機の数は
会社数×会社の平均所有率×会社あたりの平均所有数
+
学校数×学校の平均所有率×学校あたりの平均所有数
で求められると仮定します。
privateなコピー機の数は
日本の世帯数×平均世帯所有率×1世帯あたりの平均所有数
で求められると仮定します。
モデル化
会社数と学校数を求めましょう。参考書に倣います。
会社数=生産年齢人口÷会社あたりの人数
学校数=学生人口÷学校あたりの人数
このように仮定します。生産年齢人口は20-59歳で女性の半分は専業主婦と仮定します。すると,例題1・2で見てきたように20歳ごとの人口比を2:3:3:2と仮定すると,生産年齢人口は5400万人と求められます。また,会社あたりの人数は「8割が10人規模」「2割が100人規模」と仮定すれば,1会社あたり約28人となります。また,平均10人で1つのコピー機を使うと考えれば,会社のコピー機所有台数は約2.8個になります。
学生人口は,0-9歳の半分と10-19歳の人口を足し合わせたものとします。つまり,1800万人です。1学校あたりの人数は,平均的な学年数が(6+3+3+4)/4=4年ということに注意すれば,1学年あたり100人という仮定から400人ということになります。
また,世帯数に関しては例題2を借用しましょう。3人以下の世帯にはコピー機は1つ,4人以上の世帯にはコピー機は1.5個と仮定します。また,所有率は世帯の大小に関わらず50%と仮定します。
計算実行
上の公式に当てはめて計算すると
8009万台
となりました。
現実性検証
日本国民の3人に2人がコピー機を(private or publicに)所有しているという計算です。実際にはもっともっと多いと思います。というのも,publicな対象としてコンビニや図書館などの公的機関も含まれるからです。
例4:日本に電柱は何本あるか
分類としてはフェルミ推定の「ストック問題ー存在アプローチ」に該当します。面積ベースの解法で,超有名問題らしいです。実際に解法の流れに沿って解いていきましょう。
前提確認
電柱の定義を確認します。といっても電柱には種類があるわけではないため,道路脇に建てられている電柱を対象にすることにします。
アプローチ設定
電柱の数は
日本の面積÷電柱1本あたりの面積
で求められると仮定します。
モデル化
日本の面積38万㎢のうち,2割を都会,8割を田舎と仮定します。また,田舎の3割が無人地域,7割が有人地域と仮定します(都会は10割有人地域とします)。電柱は有人地域にあると仮定します。都会では時速4kmで1分歩けば,田舎の有人地域では4分歩けば電柱が見つかると仮定すれば,それぞれ電柱は$\frac{4}{30}$km四方に1つ,1km四方に1つ存在すると仮定することができます。
計算実行
上の公式に当てはめて計算すると
2250万本
となりました。
現実性検証
2018年のNPO法人電線のない街づくり支援ネットワークによる発表によると,日本にある電柱の数は3400万本だということです。少し少なく見積もり過ぎた感はありますが,まあまあ妥当な線だと思います。
例5:日本にスタバは何店舗あるか
分類としてはフェルミ推定の「ストック問題ー存在アプローチ」に該当します。面積ベースとユニットベースを合わせた解法です。実際に解法の流れに沿って解いていきましょう。
前提確認
スタバの定義を確認します。といってもスタバには種類があるわけではないため,私たちがよく見かけるスターバックスコーヒーの実店舗を対象にすることにします。
アプローチ設定
参考書の流れに沿います。スタバの数は
東京都のスタバ数×東京都の人口に対する日本の人口の比率
で求められると仮定します。つまり,スタバ数は人口に比例すると仮定しています。
モデル化
東京都のスタバ数に関しては,面積ベースで求めていきます。東京都の面積は,「赤羽ー多摩川間が約1時間」「葛西ー奥多摩間が2時間」という体感から,電車の時速を平均時速40kmとすれば,3200㎢と概算できます。また,東京の山地と平地の比率は1:3とすれば,平地の面積は2400㎢となります。スタバは平地にのみ存在すると仮定します。
東京においては,駅ごとにスタバの数は約1店舗あるとします。また,駅の間隔は3分程度とすれば,電車を平均時速40kmとすれば2km間隔となります。つまり,平均2km四方の中にスタバは2店舗あると考えられます。すると,東京都のスタバ数は以下のように求められます。
東京都の面積÷スタバ1店舗あたりの面積
この式に当てはめれば,東京都のスタバ数は300店舗と求まります。また,東京都の人口は昼間人口1500万人,夜間人口1200万人の間をとって1400万と仮定します。
計算実行
上の公式に当てはめて計算すると
2500店舗
となりました。
現実性検証
スターバックスコーヒージャパン株式会社の会社概要を見ると,店舗数は1497店舗(2019年9月30日現在)となっています。少し多く見積もり過ぎましたが,これは必ずしもスタバの数が人口に比例しないことが原因だと思われます。
例6:日本に消防署はいくつあるか
分類としてはフェルミ推定の「ストック問題ー存在アプローチ」に該当します。実際に解法の流れに沿って解いていきましょう。
前提確認
消防署の定義を確認します。といってもスタバには種類があるわけではないため,私たちがよく見かける消防署を対象にすることにします。また,消防署の役割を考えた時に,ある一定の時間で到達できる範囲に必ず1つは存在すると考えられます。この考え方では,円の面積に基づいたアプローチを仕掛けていくことになります。
アプローチ設定
参考書の流れに沿います。消防署の数は
日本の面積÷1つの消防署あたりの面積
で求められると仮定します。
モデル化
ここも参考書に沿います。日本の面積のうち,3:1の割合で山地と平地が存在していると仮定します。また,山地のうち,1:2の割合で無人地域と有人地域が存在していると仮定します。無人地域には消防署は存在しないと仮定します。また,平地を「市街地」,山地を「田舎」と捉えることで,1つの消防署が網羅する面積をそれぞれ考えていきます。
市街地では時速40kmの車で10分以内にたどり着ける範囲に消防署が平均1つあると考えます。また,田舎では時速40kmの車で20分以内にたどり着ける範囲に消防署が平均1つあると考えます。すると,市街地では約130㎢あたりに1つの消防署が,田舎では約500㎢あたりに1つの消防署があると仮定します。
計算実行
上の公式に当てはめて計算すると
1000署
となりました。
現実性検証
内閣府の防災情報のページによると,消防署は1719機関とのことです。少し少なく見積もり過ぎましたが,車で到達できる範囲が市街地では約5-10分程度,田舎でも約15-20分程度に設定するとうまくいきそうです。
例7:日本にスキー場はいくつあるか
分類としてはフェルミ推定の「ストック問題ー存在アプローチ」に該当します。実際に解法の流れに沿って解いていきましょう。また,この問題は参考書と全く同じ問題になりますが,解法を変えています。
前提確認
スキー場の定義を確認します。といってもスキー場には種類があるわけではないため,私たちがよく見かけるスキー場を対象にすることにします。
アプローチ設定
スキー場の数は
スキー場の年間のべ来客者数÷スキー場あたりの平均年間来場客数
で求められると仮定します。また,スキー場の年間のべ来場客数は以下のように求められると仮定します。
日本の人口×年間スノースポーツ頻度×スキー選択率
スキー場あたりの平均年間来場客数は,以下のように求められると仮定します。
1時間あたりのリフト乗客者数×リフト稼働時間×スキー場オープン日数÷平均リフト乗車回数
モデル化
まずはスキー場の年間のべ来客者数からモデル化していきます。日本の人口を10歳ごとにセグメント分けしていきます。若者ほどスノーボードを選ぶ傾向が高いことを反映してみます。また,大学生〜社会人始めたての人もスノースポーツをよく嗜むというイメージも反映します。また,人口比はおなじみの2:3:3:2を採用します。
| 人口 | 頻度 | 選択率 | |
| 10-19 | 1200万 | 1 | 30% |
| 20-29 | 1800万 | 2 | 30% |
| 30-39 | 1800万 | 1 | 30% |
| 40-49 | 1800万 | 1 | 60% |
| 50-59 | 1800万 | 2 | 60% |
| 60- | 2400万 | 2 | 60% |
また,1時間あたりのリフト乗客者数は,待ち行列が0として体感で平均10秒に1回2人乗りのリフトが回ってきます。ですので,1時間あたり平均360人が乗る計算になります。一方,体感ベースで1つのコースあたり15分程度滑り降りるのに時間がかかりますから,1時間で平均4回リフトに乗る計算になります。また,リフトの稼働時間は平均で9時から16時の7時間とします。また,スキー場がオープンしているのは平均4ヶ月間とします。つまり,スキー場あたりの平均来場客数は
360×7×120÷4=75600人
となります。
計算実行
上の公式に当てはめて計算すると
約1000箇所
となりました。
現実性検証
参考書では,2006年の日本自由時間研究所調べによるスキー場数を708としています。しかし,最近ではスキー場は減ってしまっていることが予想できますので,およそ600〜650程度のスキー場数だと考えられます。そうすると,約1000箇所というのは少し見積もりとしては多すぎるかも入れません。これは,各年代の人が少なくとも平均1回はスノースポーツをしているという仮定が多過ぎたということが原因だと思われます。
例8:ピアスの市場規模は?
分類としてはフェルミ推定の「フロー問題ーマクロ売り上げ推定」に該当します。実際に解法の流れに沿って解いていきましょう。
前提確認
ピアス市場の定義を確認します。ここでは,ピアスは個人が所有するものに限定して考えていきます。
アプローチ設定
ピアスの市場規模は
ピアスの平均単価×ピアスの売り上げ個数
で求められると仮定します。また,ピアスの売り上げ個数は以下のように求められると仮定します。
日本の人口×ピアス購入率×1年あたりの購入個数
モデル化
ピアスの平均単価・ピアス購入率・1年あたりの購入個数は年齢・性別のセグメント毎に異なると考えられます。そこで,以下のようにモデル化していきます。男女比は1:1とし,20歳ごとの年代別の比率は2:3:3:2とします。
| 人口 | 平均単価(男/女) | 購入率(男/女) | 購入個数(男/女) | |
| 10-19 | 1200万 | 1500/1000 | 10%/50% | 1/1 |
| 20-29 | 1800万 | 2000/2000 | 10%/80% | 1/3 |
| 30-39 | 1800万 | 3000/2000 | 10%/80% | 1/3 |
| 40-49 | 1800万 | 3000/2000 | 10%/80% | 1/3 |
| 50-59 | 1800万 | 4000/3000 | 10%/70% | 1/2 |
| 60- | 2400万 | 4000/4000 | 10%/70% | 1/2 |
計算実行
執筆中
現実性検証
執筆中
例9:割り箸の市場規模は?
分類としてはフェルミ推定の「フロー問題ーマクロ売り上げ推定」に該当します。実際に解法の流れに沿って解いていきましょう。
前提確認
割り箸市場の定義を確認します。ここでは,割り箸は個人が使うもの,団体が使うものに分類して考えていきます。また,団体は個人の集団と旅館などの宿泊施設に分けて考えていきます。
アプローチ設定
割り箸の市場規模は
割り箸の平均単価×割り箸の売り上げ個数
で求められると仮定します。また,割り箸の売り上げ個数は以下のように求められると仮定します。
日本の人口×割り箸使用率×1年あたりの購入個数
+
個人団体数×割り箸使用率×1年あたりの購入個数
+
宿泊施設数×割り箸使用率×1年あたりの購入個数
モデル化
執筆中
計算実行
執筆中
現実性検証
執筆中

















