LSTMってなんだ??
最近の機械学習で大活躍しているって聞いたけど?
今回は,LSTMを知ってみたいと思っている方や,pythonでの実装を参考にしたい方を対象とした内容になります。本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。
読みたい場所へジャンプ!
はじめに
早く結論を言いなさい!LSTMって何やねん!
となっているかと思いますが,LSTMの説明を始める前に少しだけお話しさせてください。
今やLSTMは機械学習屋さんでは知らない人の方が少ないネットワークになっています。音声認識をはじめとしたあらゆる分野のブレイクスルーを起こした革新的な技術といっても過言ではないでしょう。
しかし,実はその歴史は古く,1997年[1]に最初の原型が提案されました。多くのLSTMの解説では,勾配消失/発散が問題となっていたことからLSTMを導入しています。歴史を辿っていくという意味で,最も妥当な説明だと思います。
しかし,本記事はもう少しキャッチーにLSTMを理解してみたいという方に向けた内容になっています。具体的に言えば,LSTMが
時系列データをうまく扱えるようなネットワークなんでしょ!(知らんけど)
この程度にご存知である層の方々向けに書いていきます。
私自身の経験を少しだけお話ししておきます。音声認識や音楽情報処理の分野では,LSTMはなくてはならない存在となっています。最近になってAttentionなどの台頭もありますが,いまだにLSTMの性能は劣りません。
このような背景から,LSTMを使ってみようとは思っていたものの,多くの解説記事やPytorchのドキュメントなどを読んでも,サッパリわからないという状況でした。
特に,まずは実装だと思ってPytorchのドキュメントを読むと,絶望すると思います。だって,こんな意味わからん数式が羅列されているのですから。
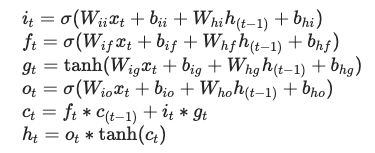
ナニコレ?!?!
何の説明もなしに,こんな数式見せられて,正しくPytorchのLSTMを使える人なんているのでしょうか。私も,最初の頃は食わず嫌いをしていて,何とかLSTMを使わずにモデルを組み立てることはできないかと試行錯誤していました。恥ずかしながら。
でもでも。思うに,このような理由からLSTMを毛嫌いして実装を避けて通っている人が多いというのは,学問の発展を妨げている気がしてなりません。「完璧に理解してから次に進む」というアプローチは,かえって遠回りになるケースが往往にしてあります。
ですので,本記事の目標は,先ほどの数式を理解して,PytorchのLSTMをある程度使いこなせるようになることを目指したいと思います。
前置きが長くなりましたが,まとめておきます。
【本記事の目標】
1.LSTMに出てくる基本的な数式を理解して
2.Pytorchで実装できるようになる
本記事の構成
本記事では,ボトムアップ形式でLSTMを理解していきます。最初に全体像を見せて詳細を説明していくトップダウン形式の説明とは異なり,徐々に詳細を詰めていくという方法をとりたいと思います。
ボトムアップを実感していただくために,LSTMの理解をレベル1〜レベル9に分けました。レベルが上がるにしたがって,どんどんLSTMの詳細に突っ込んでいきます。最初に目次を示しておきます。
●レベル1:入出力
●レベル2:ループ構造
●レベル3:展開
●レベル4:注目
●レベル5:正規化
●レベル6:状態
★コラム:WhereとHow
●レベル7:忘却
●レベル8:更新
●レベル9:最終出力
レベル1:入出力
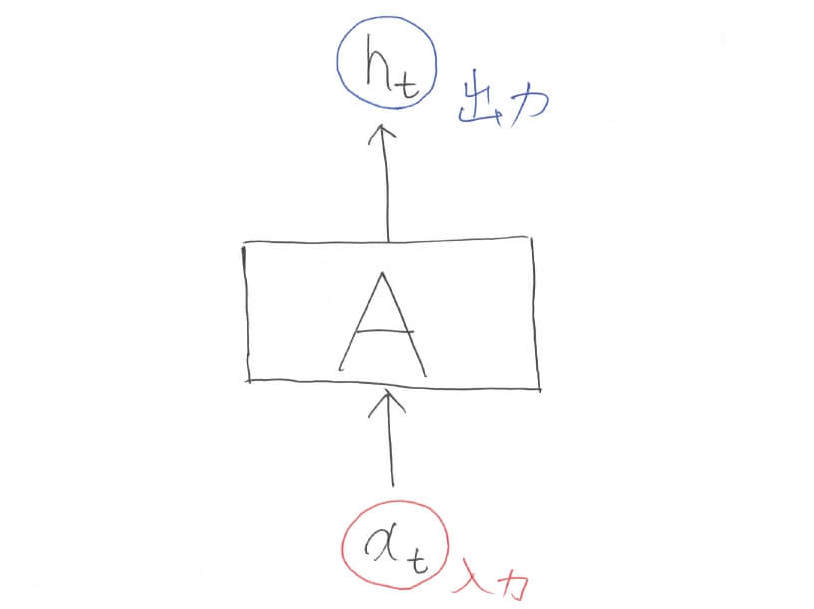
何事もまずは問題定義から入りましょう。LSTMは何をするのかというと,「入力から出力を予測する」ことを行います。機械学習には色々な問題設定(分類・クラスタリング・回帰等)がありますが,まず意識してほしいことはLSTMはNN(ニューラルネットワーク)であるということです。
LSTMは,NNの中でも系列データを得意とする再帰型ニューラルネットワークに該当します。具体的な問題設定としては,NNというくくりの中で,系列データの回帰に使われることが多い印象です。
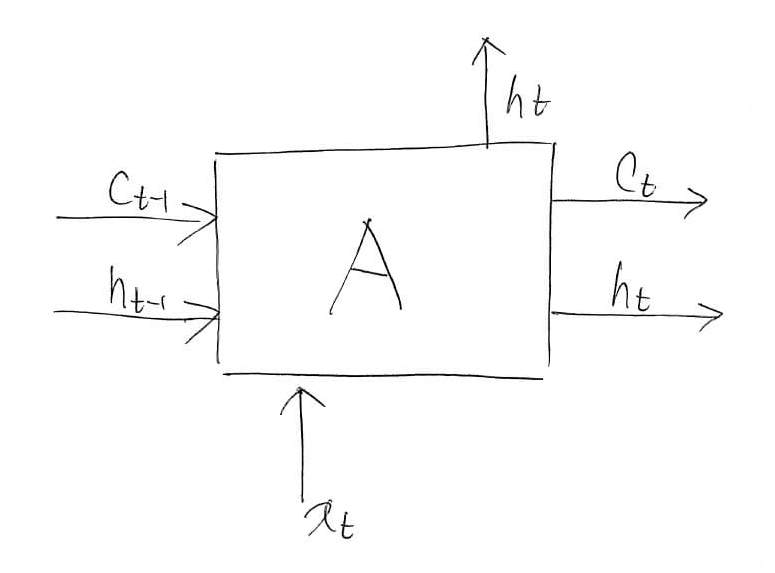
図中のAはネットワークを意味しています。まだブラックボックスにしています。添字の$t$はデータのインデックス(何番目かという情報)を表します。
【レベル1のまとめ】
\begin{align}
h_t &= A(x_t)
\end{align}
レベル2:ループ構造
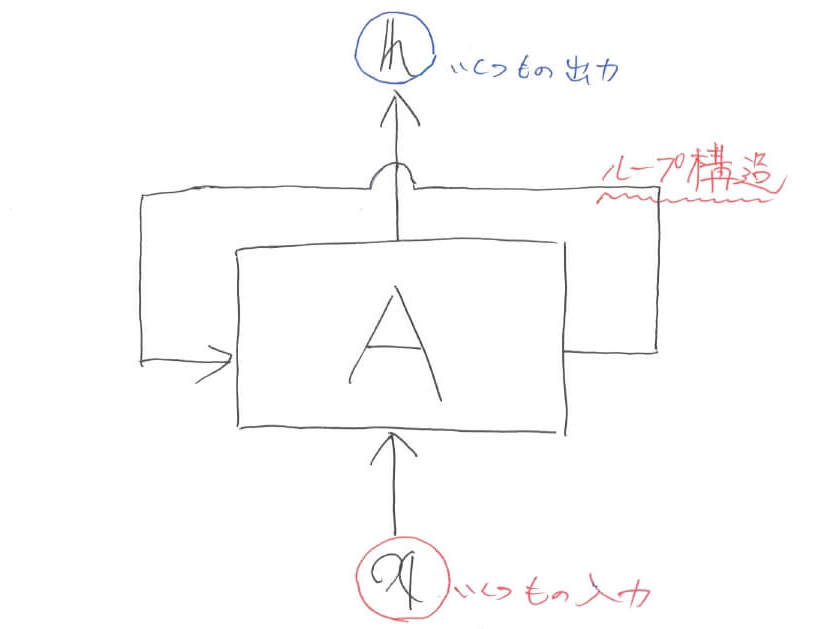
LSTM(RNN)は系列データが得意ということで,先ほどの入出力関係を複数個に拡張します。そのときに,RNNではネットワーク部にループ構造を持たせることで,系列データの情報を保持していきます。
ループ構造導入に伴って,入力はベクトルになり,出力もベクトルになっています。ただし,1つ1つのデータが複数の要素を持っているために,レベル1における入出力がベクトル,レベル2における入出力は行列になります。以下では,わざわざ太字に表すのが面倒なため,基本的に変数はベクトルだということにします。
【レベル2のまとめ】
\begin{align}
\boldsymbol{h} &= A(\boldsymbol{x})
\end{align}
レベル3:展開
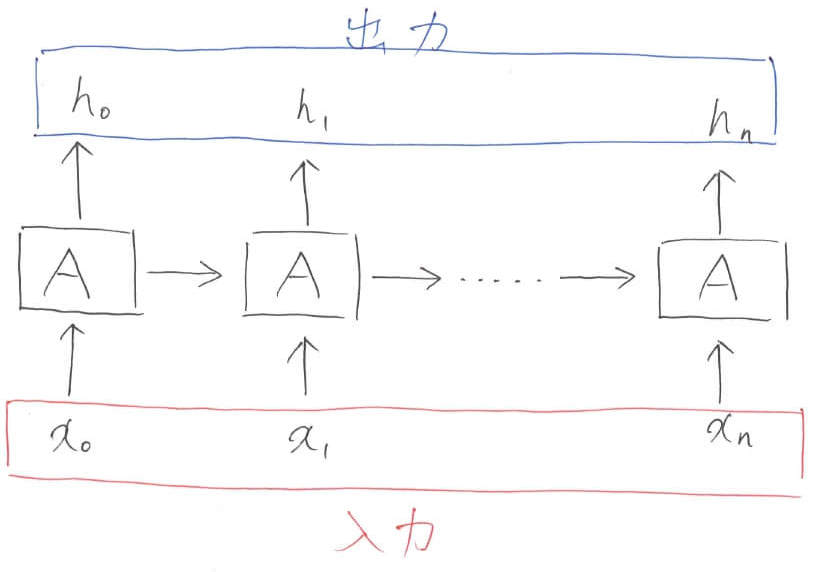
ループ構造を横に展開します。LSTMを含んだ多くの時系列ネットワークは,このように横に展開されて説明されることが非常に多いため,このレベル3の図はよく頭に入れておくといいと思います。
【レベル3のまとめ】
\begin{align}
[h_1, h_2, \ldots, h_n] &= A([x_1, x_2,\ldots, x_n])
\end{align}
レベル4:注目
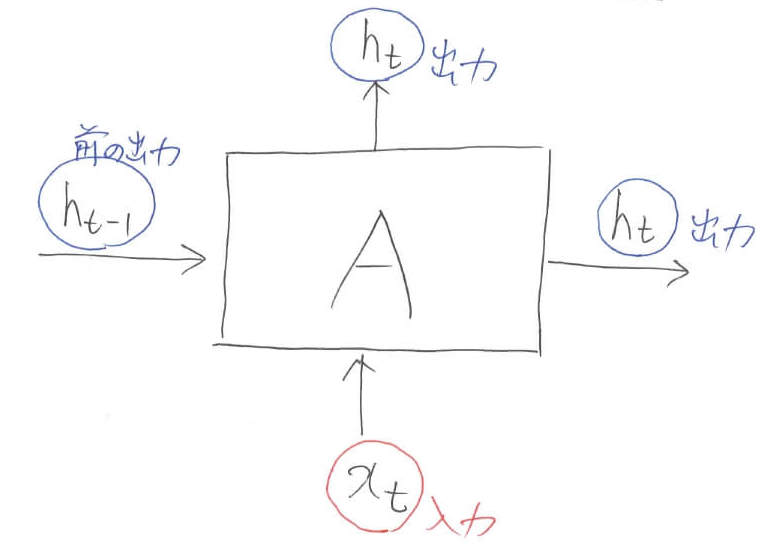
さて,横に展開されたネットワークは,全てに同じ振る舞いを示します。ですので,1つに注目すれば十分なのです。そこで,レベル1と同じように$t$番目の入出力関係に注目していきたいと思います。
レベル1と異なるのは,前の出力がネットワークに組み込まれている点です。出力がなぜ2つあるのかについては,1つの出力(上に出ている方)はネットワークの吐き出され,もう1つの出力(横に出ている方)はネットワークの内部で使い回されるからです。
【レベル4のまとめ】
\begin{align}
h_t &= A([h_{t-1}, x_t])
\end{align}
レベル5:正規化
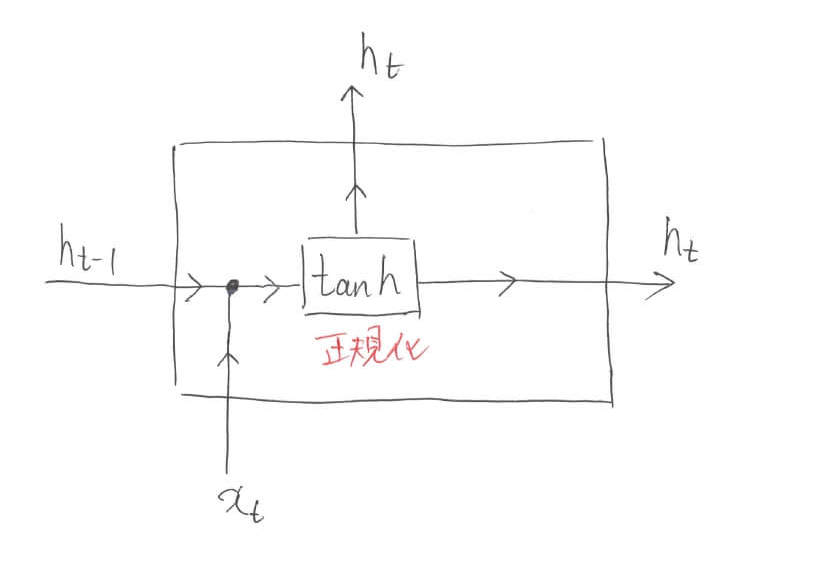
さて,徐々にLSTMの内部に突っ込んでいきます。今までブラックボックス化していたLSTMの中身を少し覗いてみましょう。ここで出てくるのが「$\tanh$」です。
$\tanh$は「ハイパボリックタンジェント」と読み,$\tan$(タンジェント)の双曲線(hyperbolic)関数を表します。NNの活性化関数としてよく用いられる関数です。
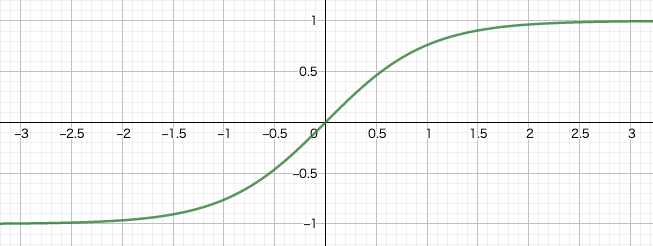
任意の実数を取る値を,$-1$から$1$の間の値に変換する役割を果たします。つまりは,正規化をしていると言って良いでしょう。
え?でも何で正規化する必要があるの?
もっともな質問です。LSTMに限った話ではありませんが,NNでは内部のパラメータが撮りうる値を制限した方が学習が上手くいきます。結局,NNの学習原理は「誤差逆伝播」です。これは何かというと,NNが吐き出した値を正解の値の誤差を「微分」という操作を介して入力まで遡って誤差を正していく手法のことを指します。
イメージしてほしいのですが,出力から入力まで遡っていくときに内部のパラメータは好き勝手な値を取ってしまうとどのようなことが起こるでしょうか。誤差の情報が「発散」してしまったり「消失」してしまったりしますね。
これを防ぐためにも,$\tanh$などの出力範囲が制限されるような関数を利用して正規化を行う必要があるのです。また,図中の黒い点「●」は,数値を連結する操作を表しています。数式中の$[\cdot]$はベクトルを結合しているという意味を表しています。
【レベル5のまとめ】
\begin{align}
h_t &= \tanh([h_{t-1},x_t])
\end{align}
レベル6:状態
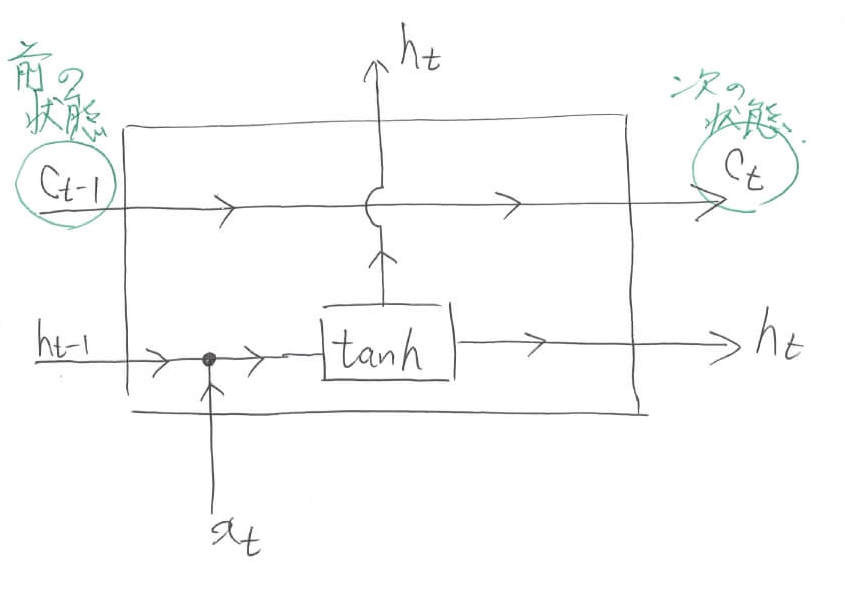
ここで,新しい概念が登場します。「状態」と呼ばれるものです。図中では$c$と表されています。こいつを内部で串刺しにしておくことで,ネットワークに情報を保持しておくことが可能になります。Understanding LSTM Networksでも指摘されているように,ベルトコンベアーをイメージすると分かりやすいでしょう。
これから内部でごにょごにょ情報をいじっていきますが,その結果を内部状態$c$に蓄えておくことで,最終結果に利用することができるようになります。数式的には,まだレベル5と変わっていません。あくまでも,前の出力$h_{t-1}$と現在の入力$x_t$を元にして次の出力$h_t$を決めているに過ぎません。
【レベル6のまとめ】
\begin{align}
h_t &= \tanh([h_{t-1},x_t])
\end{align}
コラム:WhereとHow
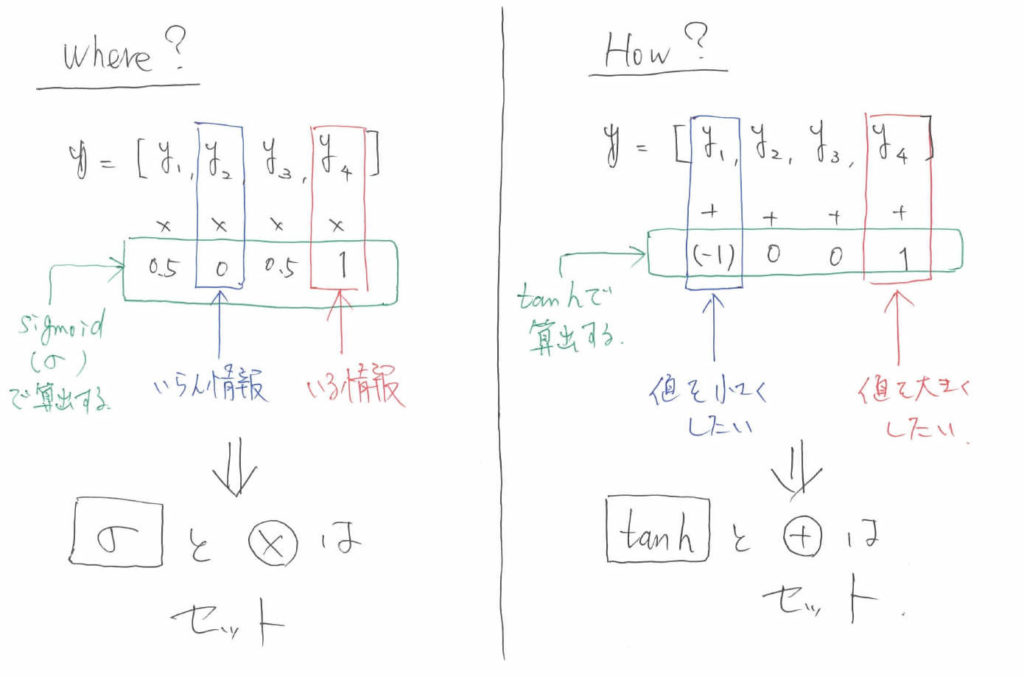
ここで一旦コラムに入ります。説明するのは,LSTMにおける「Where」 と「How」です。Whereとは「どこの情報をいじるのか」を示し,Howとは「どのように情報をいじるのか」を示します。
どこの情報をいじるのか,というのはいわばindex情報とも言い換えることができます。そして,あるベクトルのindexを指定するという操作は,算数でいうと「掛け算」に相当します。ベクトル同士の演算で言えば「要素積」に相当します。
例えば,長さ$4$のベクトル$\boldsymbol{y}$があるとします。このベクトルの2番目の情報は要らなくて,4番目の情報は必要だとしましょう。
すると,ベクトル$\boldsymbol{y}=[y_1, y_2, y_3, y_4]$に$[0.5, 0, 0.5, 1]$というベクトルの要素積を取れば,不必要なindexと必要なindexに関して情報を取捨選択できることが分かります。それ以外の$y_1, y_4$に関しては,必要か不必要かはわからないため,$0.5$という数字を掛け算することで曖昧性を表現しています。
ここで気づいてほしいのですが,掛け算に利用する要素は重要度の確率的な意味合いを持ちます。そのため,とりうる値は$0$から$1$でなくてはなりません。ここで利用される関数が「Sigmoid」です。
Sigmoidに関してはこちらの記事「【初学者向け】SoftmaxとSigmoidの関係とは。」で詳しく解説しています。Sigmoidは$\sigma$で表されます。
以上のお話から分かる通り,LSTMでは基本的に「Sigmoid」と「掛け算(要素積)」はセットで扱われます。なぜなら,重要度の確率値的な値を算出するためにSigmoidを利用し,実際に必要な値を取ってくるために要素積を利用するからです。
LSTMにおいては,もう1つセットで扱われる演算と関数があります。それが「How」に関する情報の伝達です。Howを実現する演算は「足し算」です。なぜなら,値を増やしたいなら大きい数を足せばよいですし,値を減らしたいなら小さい負の数を足せばよいからです。ベクトルで表すならば,要素ごとの足し算ということになります。
先ほど$\tanh$の説明をしたときに,基本的にパラメータのとりうる値は制限した方が良いという説明をしました。Howに関しても同様です。内部を流れる情報が基本的に$-1$から$1$の値を取ると制限しているのであれば,「どのように情報をいじるのか」についても$-1$から$1$の値を取るように設定しなくてはなりません。
ですので,どのような値を足し算するのかに関しては「$\tanh$」が決定し,実際に演算を行う際は要素和をとります。以上をまとめます。
【コラムのまとめ】
●Where?(どこの情報をいじるのか)
Sigmoid関数「$\sigma$」と「要素積」のセット
●How?(どのように情報をいじるのか)
正規化関数「$\tanh$」と「要素和」のセット
レベル7:忘却
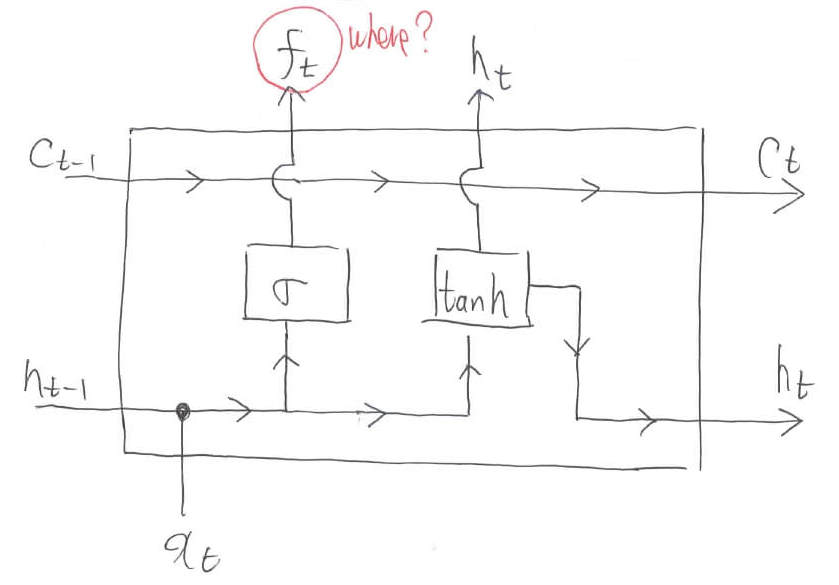
コラムの内容をぶんぶん振り回します。どこをいじるのかという「Where」の情報は,Sigmoid「$\sigma$」によって重要度的な意味合いの値$f_t$に変換されます。
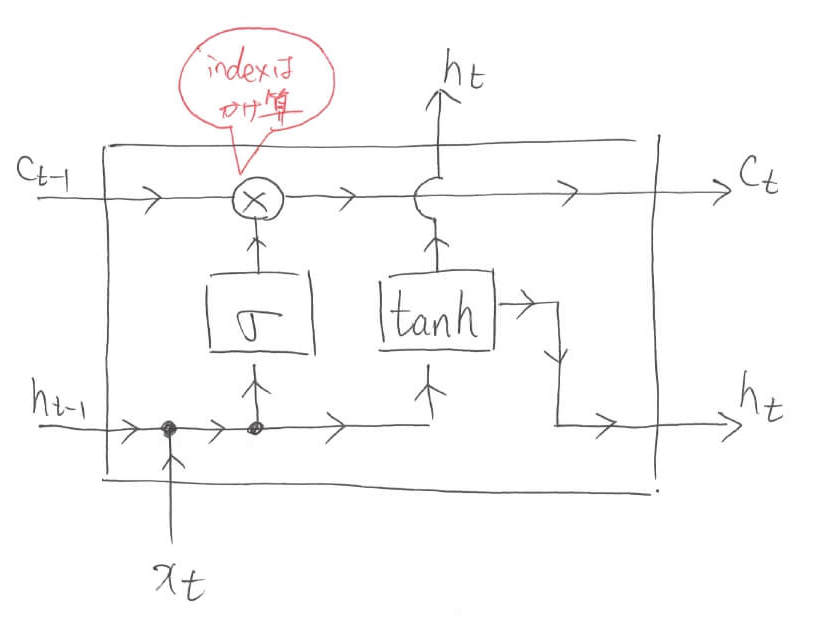
そして,Sigmoidで算出されたindex情報は,掛け算(要素積)によって内部状態$c$に保存されます。このとき,前回の内部状態$c_{t-1}$に情報を加えることによって,系列データ全体の情報を保持していくことが可能になります。まさにベルトコンベアーです。
LSTMでは,この操作で「どこの情報を忘れるんか」を学習します。ですので,忘却ゲートなんて呼ばれることもあります。数式に関して言えば,まだ出力$h_t$は内部状態を参照できていません。レベル5から何も進歩していないとも言えます。しかし,内部状態には着々と重要な情報が蓄えられています。「$\ast$」はベクトルの要素積を表します。先ほどの「●」は結合を表しましたが,今回増えた「●」はベクトルのコピーを表します。
【レベル7のまとめ】
\begin{align}
f_t &= \sigma([h_{t-1}, x_t])\\
c_t &= c_{t-1} \ast f_t\\
h_t &= \tanh([h_{t-1},x_t])
\end{align}
レベル8:更新
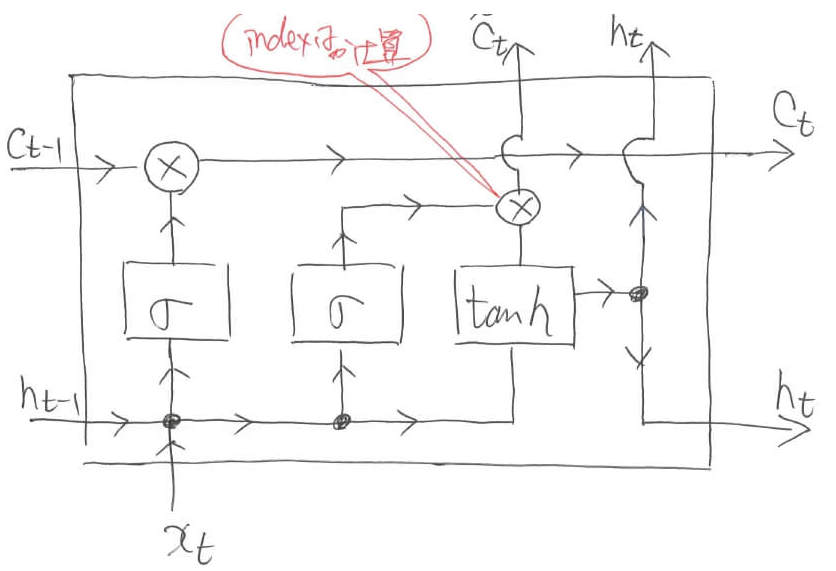
忘れさせたからには,今度は情報を付け加えなくてはなりません。ここでも,忘却のときと全く同じ操作を行います。つまり,Sigmoidによってindexの重要度を算出し,要素積によって実際に計算を行います。
そして,今回はここで終了というわけではありません。内部状態に「どのように値を更新するのか」という情報を伝達しなくてはなりません。コラムを思い出してほしいのですが,Howに対しては$\tanh$によって算出された情報を足し算するのでした。
ここで先ほどのWhereに対する操作とコラボレーションを起こします。$\tanh$によって算出された情報の重要度をSigmoidを使って算出し,要素積を取った後で,内部状態に要素和を取ります。
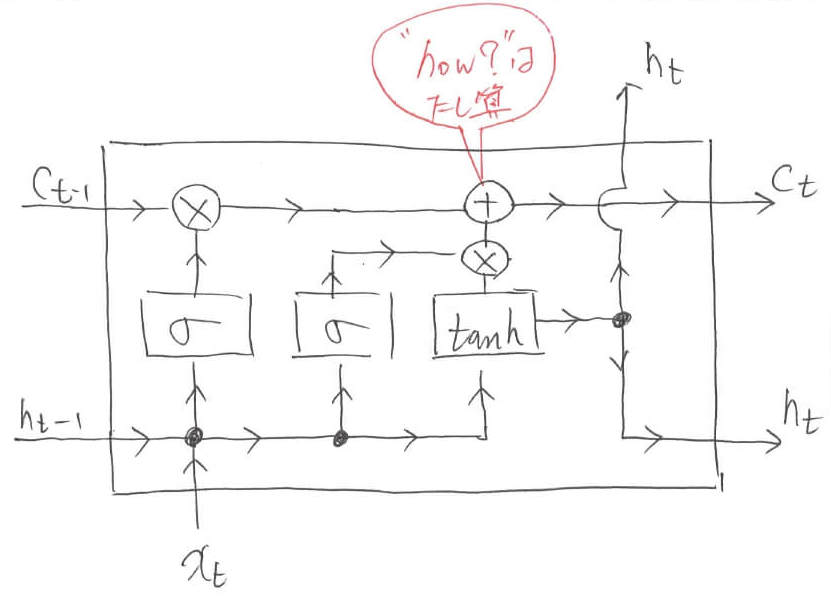
この操作によって,内部状態に「どのように値を更新するか」という情報が付け加えられます。ちなみに「$c_{t-1} = c_{t-1} \ast f_t$」のように変数をプログラミングのように値が格納される箱として捉えることにします。数学的な表記ではないため注意してください。
【レベル8のまとめ】
\begin{align}
f_t &= \sigma([h_{t-1}, x_t])\\
c_{t-1} &= c_{t-1} \ast f_t\\
\tilde{c_t} &= \sigma([h_{t-1}, x_t]) \ast \tanh([h_{t-1},x_t]) \\
c_{t} &= c_{t-1} + \tilde{c_t}\\
h_t &= \tanh([h_{t-1},x_t])
\end{align}
レベル9:最終出力
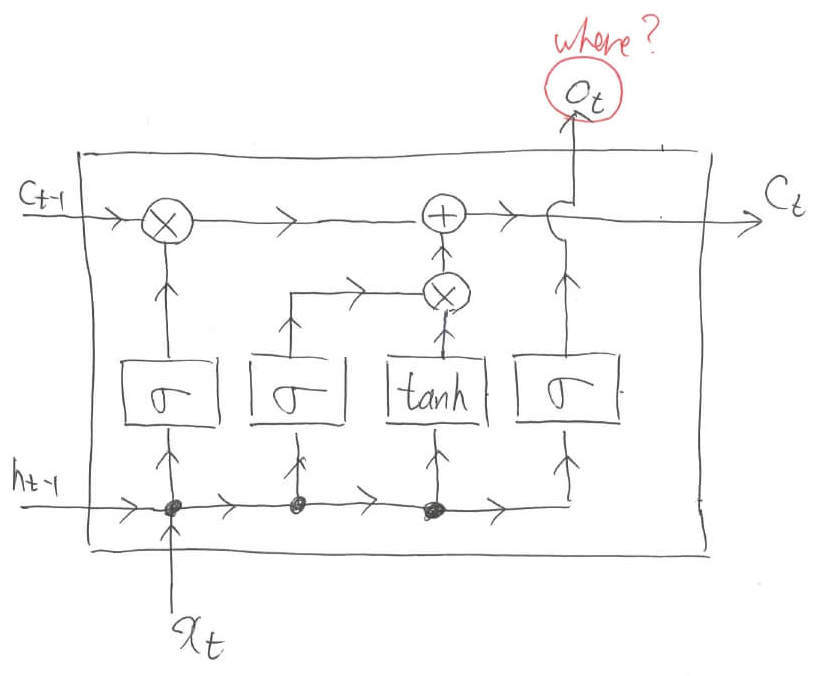
最後は,今まで蓄えてきた内部情報$c_t$の情報を利用します。例によって,Sigmoidでどこの内部情報を利用するかを決定します。そして,要素積によって実際に計算を行います。
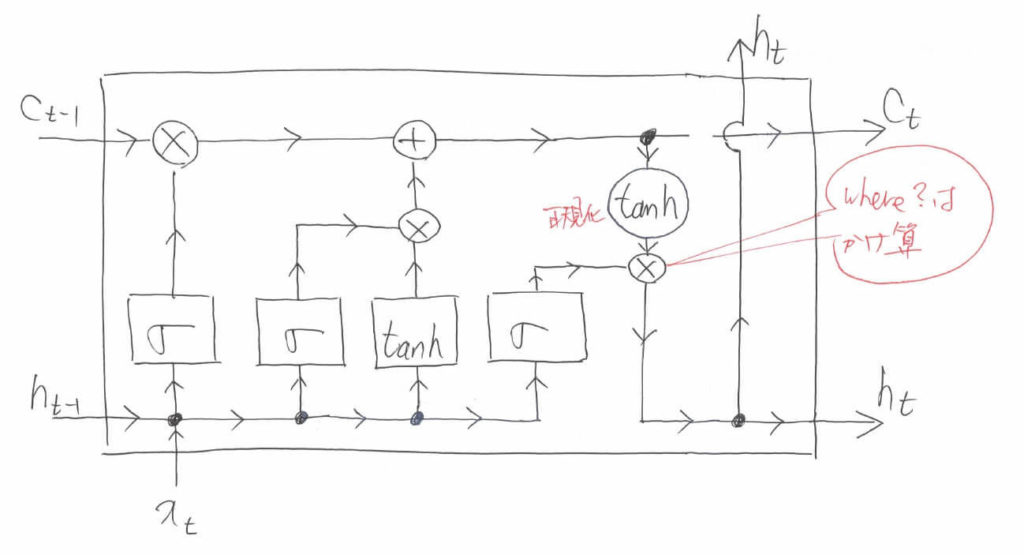
これまた例によって,要素積を取る前には$\tanh$による正規化が必要です。ちなみに,図中で四角で表されている「$\sigma$」と「$\tanh$」はニューラルネットワークで重み付け和が計算されるということを表しています。つまり,単純にSigmoid関数や$\tanh$関数に通すのではなく,$\boldsymbol{W}$という行列による重み付けと$b$というバイアス値(定数のことです)の足し算を含みますよというマークになります。
例えば,一番左のSigmoidは以下のような重み付け和とバイアス値の加算を表しています。
\begin{align}
\sigma\left(W_{i f} x_{t}+b_{i f}+W_{h f} h_{(t-1)}+b_{h f}\right)
\end{align}
一方,ただの丸で表されている箇所は演算を表します。「+」マークや「$\times$」マークが該当します。右上の「$\tanh$」は重み付け和とバイアス値の加算を含まず,単に$\tanh$に通しますよというマークを示しています。さて,数式で表していきましょう。その前に,新しい記号を定義しておきます。
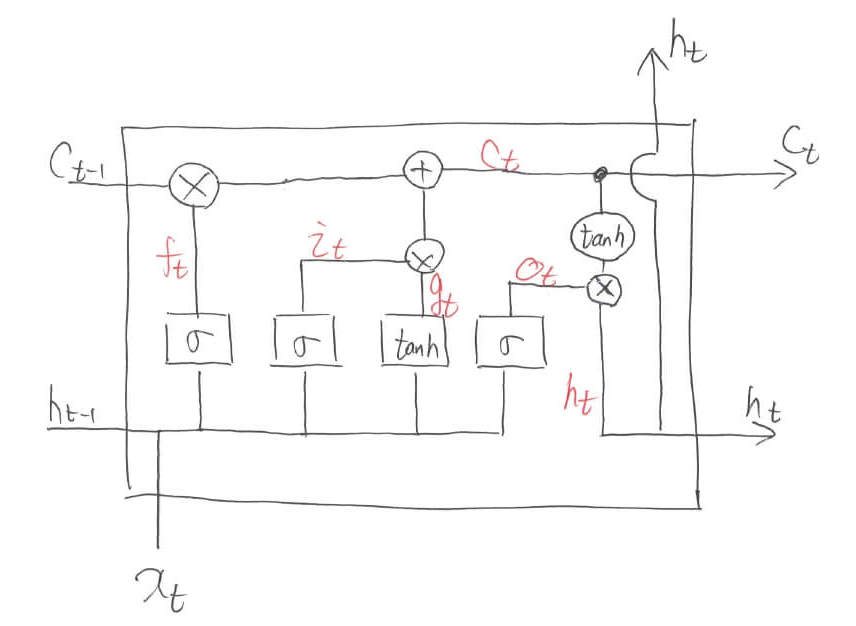
各区間におけるベクトルを上の図のように定義します。すると,以下のように入出力関係を表すことができます。
\begin{align}
i_{t} &=\sigma\left(W_{i i} x_{t}+b_{i i}+W_{h i} h_{(t-1)}+b_{h i}\right) \\
f_{t} &=\sigma\left(W_{i f} x_{t}+b_{i f}+W_{h f} h_{(t-1)}+b_{h f}\right) \\
g_{t} &=\tanh \left(W_{i g} x_{t}+b_{i g}+W_{h g} h_{(t-1)}+b_{h g}\right) \\
o_{t} &=\sigma\left(W_{i o} x_{t}+b_{i o}+W_{h o} h_{(t-1)}+b_{h o}\right) \\
c_{t} &=f_{t} * c_{(t-1)}+i_{t} * g_{t} \\
h_{t} &=o_{t} * \tanh \left(c_{t}\right)
\end{align}
あ…!この式!
はい!最初にお見せしたPytorchの公式ドキュメントの式と同じですね。
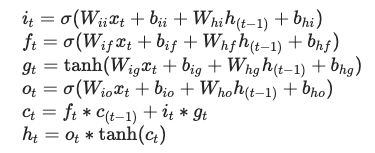
これで,ようやくLSTMのブラックボックスを説明し終わりました。最後に,簡単にLSTMを振り返っておきます。再び,LSTMの内部をブラックボックス化すれば,以下のような図に表されることが分かります。
Pytorch実装
最後に,簡単なLSTMの実装方法をお伝えしておきます。主要部分だけ抜き出していきます。以下のようなネットワークを設計します。
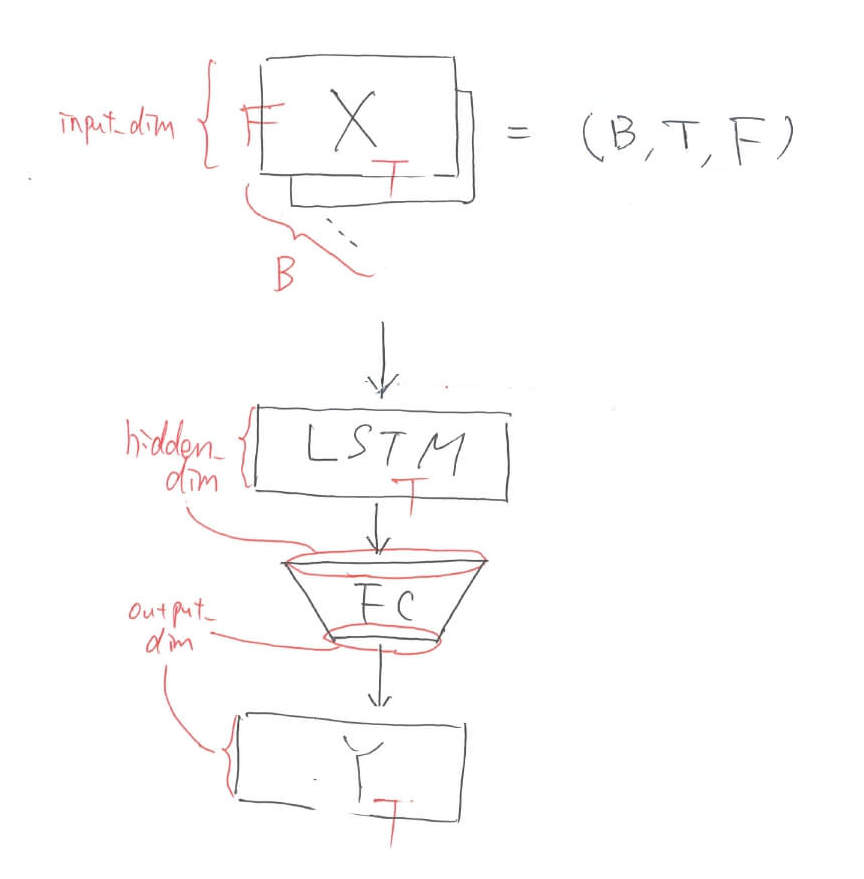
LSTMネットワークのクラス定義
class LSTM_BASIC(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(LSTM_BASIC, self).__init__()
self.lstm = nn.LSTM(input_dim, hidden_dim, num_layers=1, batch_first=True, bidirectional=False)
self.fc = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
x = self.lstm(x)
x = self.fc(x)
return xPytorchのネットワークの記法にしたがってLSTMを用いたネットワークを記述していきます。LSTMのパラメータとして「input_dim, hidden_dim, num_layers, batch_first, bidirectional」があります。input_dimとoutput_dimは各データの次元数です。データの個数ではないため注意が必要です。
num_layersはLSTMを何層重ねるかといった引数です。batch_firstは入力テンソルの軸の順番を「(バッチ数,特徴量次元数,データ数)」とするための引数です。デフォルトでは「(データ数,バッチ数,特徴量次元数)」です。何故かこんな順番なのかは謎です。forwardにはLSTMに通した後にFC層に突っ込むということを書きます。
学習
model = LSTM_BASIC(input_dim=10, hidden_dim=5, output_dim=3)
num_epoch = 100
for epoch in range(num_epoch):
# x: (B, F, T)の大きさ。
# 今回はBは適当,Fは10次元,Tも適当と想定。
~~~~~~~~~~
y, (h_n, c_n) = model(x)
# こうするとyが(B, 3, T)として出てきます。
# 2つ目の返り値(h_n, c_n)は本記事でいう([h_1, h_2,...,h_n],[c_1, c_2,..., c_n])に相当学習for文の中では,いつも通りmodelをインスタンス化して呼び出せばOKです。
[1] Hochreiter, Sepp, and Jürgen Schmidhuber. “Long short-term memory.” Neural computation 9.8 (1997): 1735-1780.
[2] http://colah.github.io/posts/2015-08-Understanding-LSTMs/






















めちゃくちゃ分かりやすかったです!
tgaさま
非常に嬉しいお言葉ありがとうございます…!!
業務で取り組む機会がありLSTMの記事をいろいろと読みあさりましたが、書いていただいた記事が最もわかりやすかったです!
ありがとうございます!
くり様
ありがたいお言葉身に沁みます。拙い箇所もありますので、どうぞご参考程度におさめていただけますと幸いです。