pythonで簡単な音声認識をやってみたいぞ。
そもそも何から始めればいいのかしら。
今回は,基本的な音声認識をpythonで行う方法をお伝えしていこうと思います。本記事はpython実践講座シリーズの内容になります。その他の記事は,こちらの「Python入門講座/実践講座まとめ」をご覧ください。

お題
FFTをpythonで実装してみよう。
流れ
今回対象とするデータは「あいうえお」ではなく,データ長が1024である合成サイン波とします。なぜなら,DFTのデータ長が2のべき乗のときに,効率的な再帰計算により高速フーリエ変換が可能になるからです。
実際に合成サイン波を作ってみましょう。
import numpy as np
import matplotlib.pyplot as plt
# データ長
N = 128
x = np.arange(N)
# 周期
t1 = 10
t2 = 20
t3 = 30
# 3つの周期の重ね合わせ
y = np.sin(t1 * 2 * np.pi * (x/N)) + np.sin(t2 * 2 * np.pi * (x/N)) + np.sin(t3 * 2 * np.pi * (x/N))
# 可視化
plt.plot(x, y)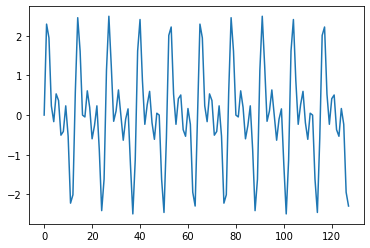
FFT(高速フーリエ変換)
詳しい導出は省略させていただきますが,簡単に導入しておきます。まず,離散フーリエ変換において$e^{-i\frac{2\pi \omega n}{N}}=W_N^{n}$とおきます。すると,離散フーリエ変換は以下のように表されます。
\begin{eqnarray}
X[\omega] &=& \sum_{n=0}^{N-1} x[n] W_N^{n\omega}
\end{eqnarray}
そして,ここから少し天下り的なのですが,離散フーリエ変換の式を偶数番目のデータ点で行った場合と,奇数番目のデータ点で行った場合に分けます。データ長が2のべき乗であるから,半分ずつに分けられますね。
\begin{eqnarray}
X_{even}[\omega] &=& \sum_{n=0}^{\frac{N}{2}-1} x[2n] W_{\frac{N}{2}}^{n\omega}\\
X_{odd}[\omega] &=& \sum_{n=0}^{\frac{N}{2}-1} x[2n+1] W_{\frac{N}{2}}^{n\omega}
\end{eqnarray}
このとき,$X_{even}[\omega]$,$X_{odd}[\omega]$,$W_N^{n}$に規則性が現れます。この規則性こそが高速フーリエ変換を「高速」たらしめる所以です。
\begin{eqnarray}
X_{even}[\omega] &=& X_{even}[\omega + \frac{N}{2}]\\
X_{odd}[\omega] &=& X_{odd}[\omega + \frac{N}{2}]\\
W_N^{n} &=& -W_N^{n+\frac{N}{2}}
\end{eqnarray}
以上を踏まえると,離散フーリエ変換を再帰的に計算することができます。まず,離散フーリエ変換を奇数部分と偶数部分で表してみましょう。偶数部分はインデックス0から始まりますので,偶数部分に奇数部分の変形版を足し合わせることで元の離散フーリエ変換を実現するという方針です。
\begin{eqnarray}
X[\omega] &=& X_{even}[\omega] + X_{odd}[\omega]W_N^{n}
\end{eqnarray}
この式に先ほどの周期性を適用すると,高速フーリエ変換が完成します。前半部分と後半部分が同時に求まっていくイメージです。
\begin{eqnarray}
X[\omega] &=& X_{even}[\omega] + X_{odd}[\omega]W_N^{n}\;(\omega=0,\cdots,\frac{N}{2}-1)\\
X[\omega+\frac{N}{2}] &=& X_{even}[\omega] – X_{odd}[\omega]W_N^{n}\;(\omega=0,\cdots,\frac{N}{2}-1)
\end{eqnarray}
実装
import numpy as np
def FFT(x):
N = x.shape[0]
# 再起動作の一番最後
if N==1:
return x[0]
x_even = x[0:N:2]
x_odd = x[1:N:2]
# ここで再帰動作をする
X_even = FFT(x_even)
X_odd = FFT(x_odd)
# DFTと同じようにWを求める
W = []
for t in range(N//2):
W.append(np.exp(-1j * ((2*np.pi*t) / N)))
W = np.array(W)
# ここで型をcomplexに指定しないとエラーを吐くので注意
X = np.zeros(N, dtype="complex")
X[0:N//2] = X_even + W*X_odd
X[N//2:N] = X_even - W*X_odd
return X結果
# 実行
Y = FFT(y)
# 結果は複素数なので実部と虚部に分けて可視化
Y_real = np.abs(Y)
Y_imag = np.imag(Y)
plt.plot(np.arange(0, Y_real.shape[0]), Y_real)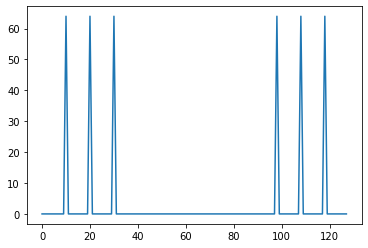
DFTと同じ結果になりましたね。
plt.plot(np.arange(0, Y_real.shape[0]), Y_imag)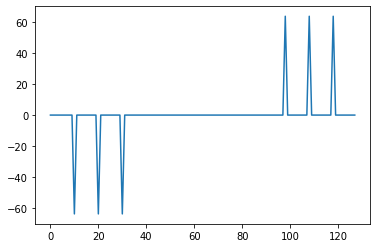
DFTと同じ結果になりましたね。ちなみに,「np.fft.fft」で試しても全く同じ結果が得られます。
高速逆フーリエ変換
せっかくなので逆変換をしてみましょう。高速フーリエ変換の逆変換は非常に単純です。逆変換は,以下のように定義されます。
\begin{eqnarray}
x[n] &=& \frac{1}{N}\sum_{n=0}^{N-1} X[\omega] W_N^{n\omega}
\end{eqnarray}
この式を変形していきます。
\begin{eqnarray}
\frac{1}{N}\sum_{n=0}^{N-1} X[\omega] W_N^{n\omega} &=& \frac{1}{N}\overline{\sum_{n=0}^{N-1} \overline{X[\omega]} W_N^{-n\omega}}
\end{eqnarray}
つまり,「FFTの結果の複素共役を取り」「普通のFFTを行い」「その結果を再び複素共役にして」「Nで割る」ことによって逆変換が可能になります。実際に行ってみましょう。
実装
def IFFT(X):
X = X.conjugate()
x = FFT(X)
return (1/N) * x.conjugate()今回は見やすいようにデータを作り直してみます。
N = 1024
x = np.arange(N)
t = 10
y_origin = np.sin(t * 2 * np.pi * (x/N))
plt.plot(x, y_origin)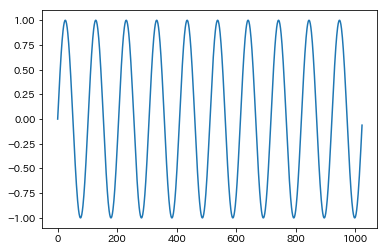
Y = FFT(y_origin)
y_recover = IFFT(Y)
y_recover_real = np.real(y_recover)
plt.plot(np.arange(y_recover_real.shape[0]), y_recover_real)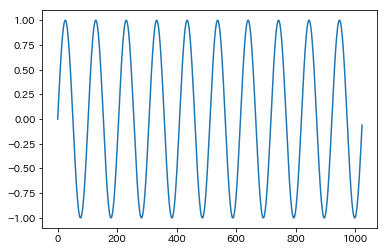
時間比較
せっかくなので,DFT・FFT・np.fft.fftの速度を比較してみましょう。
t1 = time.time()
Y = DFT(y)
t2 = time.time()
elapsed_time = t2-t1
print("経過時間:{elapsed_time}")
t3 = time.time()
Y = FFT(y)
t4 = time.time()
elapsed_time = t4-t3
print("経過時間:{elapsed_time}")
t5 = time.time()
Y = np.fft.fft(y)
t6 = time.time()
elapsed_time = t6-t5
print("経過時間:{elapsed_time}")Output:
経過時間:3.5613720417022705
経過時間:0.04334902763366699
経過時間:0.00020003318786621094圧倒的にDFTの計算が遅いですね。今回のFFTの実装ではfor文を使ってしまいましたので,nmpyのfftよりも時間がかかってしまっています。


















