【レビュー/内容まとめ】ベイズ推論による機械学習入門＜第２章＞

本記事は，新たなベイズ学習の入門書として最近注目を集めている「ベイズ推論による機械学習入門」のレビューと内容まとめになります。各章・各節ごとに内容をまとめていきます。

 

２.１ 期待値

期待値計算の定義を示します。そこから，「平均」「分散」「エントロピー」「KLダイバージェンス」の定義を期待値を利用して示して本節は終了です。

 

２.２ 離散確率分布

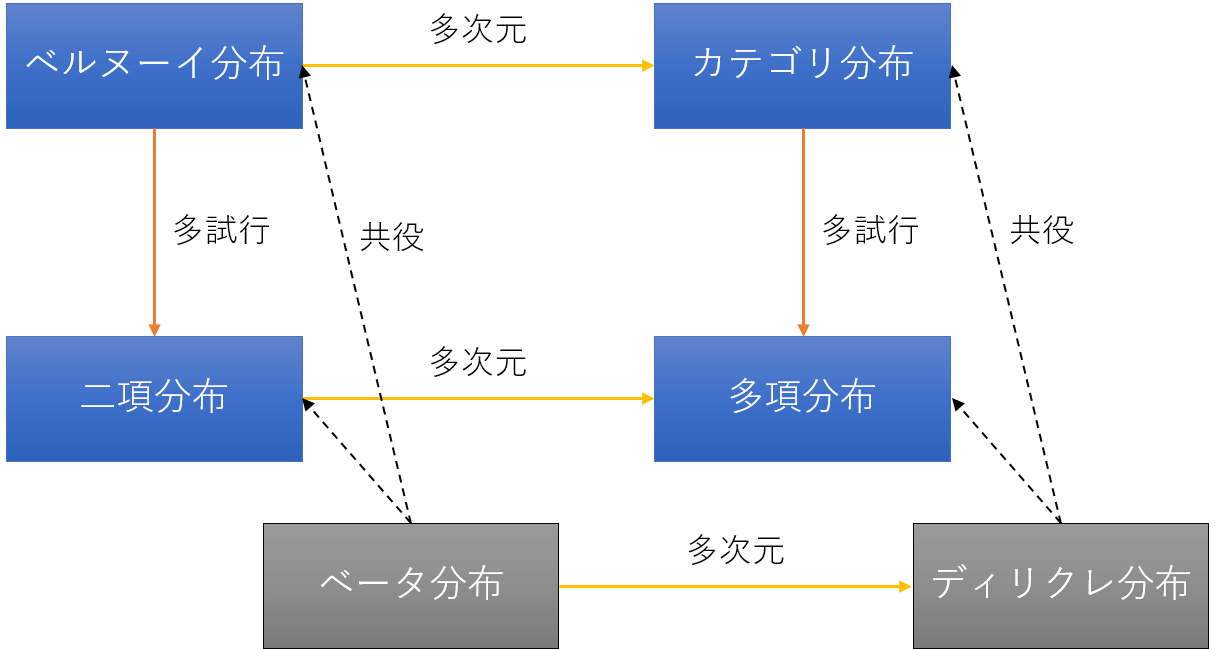
代表的な離散確率分布として「ベルヌーイ分布」「二項分布」「カテゴリ分布」「多項分布」「ポアソン分布」の確率分布の定義を示します。各分布について，期待値と分散を確認します。さらに，多項分布は二項分布を多次元化したもの，カテゴリ分布を多試行化したものであることを確認します。

 

２.３ 連続確率分布

代表的な連続確率分布として「ベータ分布」「ディリクレ分布」「ガンマ分布」「ガウス分布」「ウィシャート分布」の確率分布の定義を確認します。それぞれについて，期待値/エントロピー/KLダイバージェンスを確認します。

さらに，ベータ分布はベルヌーイ分布と二項分布の平均に関する共役事前分布であり，同様にディリクレ分布はカテゴリ分布と多項分布の共役事前分布であることに言及します。ガンマ分布はポアソン分布のパラメータに関する共役事前分布であり，加えて１次元ガウス分布の分散の逆数に関する共役事前分布であることも確認します。ウィシャート行列は多次元ガウス分布の共分散行列の逆行列を生成する分布であることも確認します。

 

レビュー

非常に分かりやすい章でした。それぞれを個別に理解するのではなく「多試行化」「多次元化」「共役事前分布」という軸で結び付けている点が初学者の取り組みの手助けとなっています。ただし，この章の段階では「共役事前分布」に関して知識が全くない状態ですので，少しモヤモヤが残ったまま章を終えることになりそうです。この章を読むことで，ベイズ学習の事前分布でディリクレ分布がよく用いられる理由がよく分かりました。