この記事では,研究のサーベイをまとめていきたいと思います。ただし,全ての論文が網羅されている訳ではありません。また,分かりやすいように多少意訳した部分もあります。ですので,参考程度におさめていただければ幸いです。
間違えている箇所がございましたらご指摘ください。随時更新予定です。他のサーベイまとめ記事はコチラのページをご覧ください。
本記事の内容
本記事では,「Neural Machine Translation by Jointly Learning to Align and Translate」[Dzmitry Bahdanau+ 2014]を日本語で要約したものを簡単にまとめていきます。
要旨
最初はお決まりのパターンで,機械翻訳の分野はニューラルネットワークの登場によって飛躍的に進歩したという紹介。しかし,ニューラルネットを用いたモデルにも,欠点があると筆者は指摘しています。それは,「長い文章に対応できないこと」だとしています。
ニューラルネットを用いたモデルの一般的な形は,エンコーダ(符号化部)とデコーダ(解読部)を併せ持つシステムです。つまり,ある文章を入力として与えた時に,エンコーダ部で何かしらのベクトル表現に変換して,デコーダ部でそのベクトル表現を他の言語で表すというような流れになっています。エンコーダ部は,翻訳対象の言語情報を圧縮するようなイメージで,デコーダ部は圧縮された情報を他の言語で読み取るようなイメージです。(※あくまでもイメージ)
それでは,なぜ従来の方法では長い文章に対応できなかったのでしょうか。それは,エンコーダ部で「常に同じ長さの」ベクトル表現に変換していたからなのです。短い文章であれば,変換後のベクトル表現はしっかりと情報を保持していると考えられますが,文章が長くなればなるほど,変換後のベクトル表現は相対的に情報がそぎ落とされてしまいます。
そこで,本論文では「確率的な重み付け」を利用して,エンコーダの出力を固定長に制限しないようにすることで,大幅な精度UPを実現しています。
モデル詳細
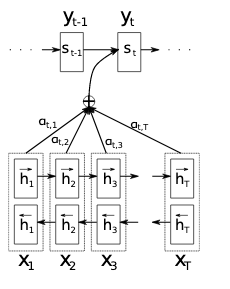 出典:「Neural Machine Translation By Jointly Learning To Align And Translate」
出典:「Neural Machine Translation By Jointly Learning To Align And Translate」最初に,モデルの表現に使用する数式を列挙していきたいと思います。従来のRNNを利用した機械翻訳のモデルは,以下のように表されます。
\begin{eqnarray}
\boldsymbol{x} &=& (x_1, \cdots, x_{T_x})\\
h_t &=& f(x_t, h_{t-1})\\
c &=& q(\{ h_1, \cdots, h_{T_x} \})\\
p(\boldsymbol{y}) &=& \prod_{t=1}^Tp(y_t|\{ y_1, \cdots, y_{t-1} \}, c)\\
&=& g(y_{t-1}, s_t, c)
\end{eqnarray}
順々に説明していきますね。$x_i$は単語,$\boldsymbol{x}$は文章を表しています。$h_j$は$j$番目の入力に対する隠れ状態(hidden state),$c$は隠れ状態に基づいて生成されるベクトルを表しています。
そして,出力される翻訳$\boldsymbol{y}$は,$y_{t-1}$,$c$,そして出力に対する隠れ状態$s_t$によって決定されます。$q$と$g$は適当な非線形変換を表しています。
そして,本論文で紹介されているモデルは,上記モデルに少しアレンジを加えます。(著者は抜本的な改変だと主張していますが)
\begin{eqnarray}
p(y_i|\{ y_1, \cdots, y_{i-1} \}, \boldsymbol{x}) &=& g(y_{i-1}, s_i, c_i)\\
s_i &=& f(s_{i-1}, y_{i-1}, c_i)\\
c_i &=& \sum_{j=1}^{T_x}\alpha_{ij}h_j\\
\alpha_{ij} &=& \frac{\exp(e_{ij})}{\sum_{k=1}^{T_x}\exp(e_{ik})}\\
e_{ij} &=& a(s_{i-1}, h_j)
\end{eqnarray}
焦らずに,ゆっくりみていきましょう。まず,$y_i$を推論する際に,新モデルでは条件付き確率に入力$\boldsymbol{x}$を利用しています。また,$c$は各出力の隠れ状態数に対応する$c_i$という形で定義されています。
具体的には,入力の隠れ状態の線形重み付け和として定められています。ここが,本論文のポイントで,ソフトに各入力の要素を利用することで,従来の固定長のベクトルに情報を圧縮するというハードなモデルの弱点を克服しています。
重み付けのための$\alpha_{ij}$は,ソフトマックス的に定められています。何をソフトマックスに通すかというと,式(10)のように定められた$e_{ij}$を利用します。式(10)において$a$は,モデル全体と一緒に学習されるフィードフォワードニューラルネットワークとされています。つまり,翻訳機として入力に対して,正しい重み付けができるように学習されたネットワークから出力される$e_{ij}$を用いるということです。
ちなみに,$f$は$q$や$g$と同様に,適当な非線形変換を表しています。
実験結果
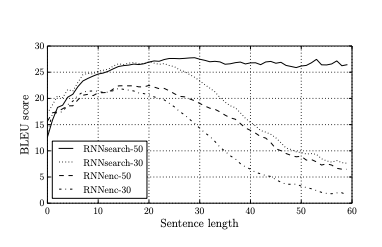 English-French task
English-French task本論文では,ACL WMT ’14によるパラレルコーパスを利用して,英語ーフランス語の翻訳タスクをタスクとして行いました。結果としては,従来法の欠点である「長い文章に対応できない」という部分を見事改善することができました。それだけでなく,文章の長さに関わらず,良い精度を発揮することができました。
まとめ
著者は,ニューラルネットワークに基づく機械翻訳の抜本的なモデル改善に貢献したと主張しています。やはり,ハードをソフトにという視点は大切なのですね。頻度主義者とベイジアンの議論を思い起こされます。
実際に,論文中にもあるように,英語の「The」はフランス語で「le」「la」「les」「l’」に相当するため,ソフトな決定方法でなければうまく翻訳することができないでしょう。このような視点からも,最近ベイジアンが流行っていることにも納得がいくような気がします。
Bahdanau, Dzmitry, Kyunghyun Cho, and Yoshua Bengio. “Neural machine translation by jointly learning to align and translate.” arXiv preprint arXiv:1409.0473 (2014).
















