本記事は新ブログへ移行しました。
ご質問やご指摘は以下のページへお願い致します。
(以下の内容は古いため正確性は全く保証できません)
本記事は教養記事シリーズその53です。その他の教養記事は【超初心者向け】3分で分かる!教養記事シリーズ目次をご覧ください。
待ち行列とは
用語解説
先に結果を説明
理論的な背景も少しだけ
待ち行列
待ち行列とは,名前の通り「待っている人の行列」を指します。行列は行列でも,数学で扱う行列(Matrix)ではなく,人が並ぶ行列(queue)を指しています。情報学を専攻されている方であれば,「キュー」と「スタック」を習ったことがあるかもしれません。待ち行列の行列は,その「キュー」に相当します。
行列に並ぼうとする人の素朴な疑問として,「私はあとどれくらい待てばいいんだろう」と思いますよね。待ち行列理論というのは,待ち時間を解析するために作られたモデルになります。実際のところは,人間の待ち時間ではなく,コンピュータ内部の構造などに幅広く応用されたりしています。
ケンドールの記号
待ち行列理論において,先人たちは様々なモデルを考えてきました。多くのモデルを統一的に表すことができる便利な記法を「ケンドールの記号」と呼びます。
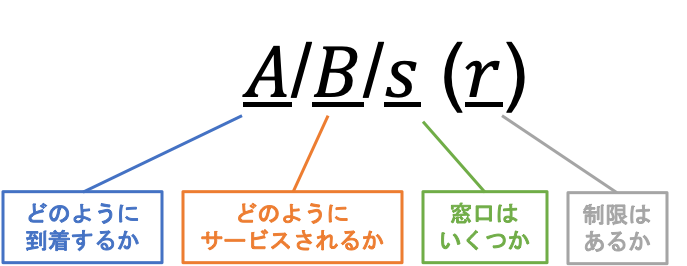 ケンドールの記号
ケンドールの記号待ち行列理論は,非常にバリエーションの豊富なモデルです。その中でも,一番シンプルかつ分かりやすいモデルが,M/M/1モデルになります。
M/M/1モデルのMは無記憶の「Memoryless」,もしくはマルコフ過程の「Markovian」が由来になっています。どちらも表したい意味は同じで,要するにイベントの発生が一様であることを示しています。
となりますよね。イベントというのは,待ち行列に人が入ってくるという事象や,待ち行列の先頭が窓口に対応してもらうという事象を表しています。これらの事象が一様,つまり完全にランダムな形で起こるという状況を考えているのが,M/M/1モデルになります。
他にも,窓口数が2つの「M/M/2モデル」やアーラン分布を利用した「M/E/1モデル」,規則的な到着を考えた「D/M/1モデル」や行列長に制限をつけた「M/M/1(N)モデル」などがあります。
用語解説
それでは,ここからM/M/1モデルについて詳しく見ていきたと思います。M/M/1モデルでは,以下の用語を利用します。少し難しいと感じるかもしれませんが,この用語さえクリアしてしまえばM/M/1をクリアしたもほぼ同然です。
【用語説明】
●平均到着率:$\lambda$[人/時間]
●平均サービス率:$\mu$[人/時間]
●平均稼働率:$\frac{\lambda}{\mu}$
ひとつずつ見ていきます。平均到着率というのは,単位時間あたりに到着する人数のことを指しています。例えば,ある病院に患者が1時間で平均100人来る場合,平均到着率は100となります。
平均サービス率というのは,単位時間あたりにサービスを受けることのできる人数のことを指します。たとえば,1人の医者が1時間で平均5人を診察できる場合,平均サービス率は5となります。
さて,平均稼働率というのは,平均サービス率に対する平均到着率の割合を指しています。つまり,想定している状況がどれくらい「いっぱいいっぱいなのか」を示していると言えます。たとえば,先ほどの例で言えば,ある病院に平均到着率100で患者が来て,医者は1人で平均サービス率5で診察するとします。
このとき,平均稼働率は「100÷5=20」となり,とてもいっぱいいっぱいいであることが分かります。
先に結論
結論から言うと,M/M/1モデルを考えることで「平均何人分待つのか」を知ることができます。その上で,「平均どれくらい待つことになるのか」を知ることもできます。
【M/M/1モデルから分かること】
●平均何人分待つのか
\begin{eqnarray}
\frac{\rho}{1-\rho}
\end{eqnarray}
●平均どれくらい待つのか
\begin{eqnarray}
\frac{\rho}{1-\rho} \cdot T_s
\end{eqnarray}
練習問題
今流行りのタピオカ屋さんでシミュレーションしてみましょう。
あるタピオカ屋さんでは,お客さんが平均3分間隔でやって来ます。タピオカ屋さんの店員は「タピさん」1人しかおらず,タピさんは1人のお客さんに対して平均2分でタピオカを提供することができます。(ただし,到着人数はポアソン分布,提供数は指数分布に従うとします)
最後の()内の文章は,よく分からなければ飛ばしてもOKです。それでは,先ほどの公式を利用して「平均何人待つのか」と「平均あとどれくらい待てばよいのか」を求めてみましょう。まずは,平均到着率$\lambda$と平均サービス率$\mu$から求めていきましょう。単位に注目すれば,与えられた数値の逆数を取ればよいことが分かります。
\begin{eqnarray}
\lambda &=& \frac{1}{3}\\
\mu &=& \frac{1}{2}
\end{eqnarray}
次に,平均稼働率$\rho$を求めていきます。
\begin{eqnarray}
\rho &=& \frac{\lambda}{\mu}\\
&=& \frac{2}{3}
\end{eqnarray}
したがって,このタピオカ屋さんでは平均$\frac{2/3}{1-2/3}=2$人分待たなければならないことが分かります。1人あたりの平均サービス時間はタピさんがタピオカを提供する2分なので,結局以下のようにして待ち時間を計算することができます。
\begin{eqnarray}
2 \cdot 2 &=& 4
\end{eqnarray}
つまり,このタピオカ屋さんでは,平均して4分待てばいいなということが分かりました。
理論的な背景
ここからは,ちょびっとだけ理論的な背景をお話ししていきます。まず,M/M/1モデルにおける分布の仮定の仕方についてです。先ほど,「ポアソン分布」と「指数分布」という言葉が出て来ましたね。実は,M/M/1モデルでは,この2つの分布が大活躍します。
ポアソン分布というのは「単位時間あたりの生起確率」,指数分布というのは「生起間隔の確率」を表します。言葉で説明すると混乱してしまいますよね。以下の説明が一番しっくり来ると思います。
●ポアソン分布
単位時間あたり平均$\lambda$回起こる事象
●指数分布
平均$\frac{1}{\lambda}$単位時間あたりに1回起こる事象
つまり,ポアソン分布はある事象の「回数」に注目する一方で,指数分布は「時間」に注目しているのです。M/M/1モデルの文脈に直せば,お客さんが単位時間あたりに到着する「回数」を表すのがポアソン分布で,窓口が1人あたりにかける「時間」を表すのが指数分布なのです。
もう一点,非常に重要なポイントがあります。それは,Mの由来となった「無記憶性」という部分です。無記憶というのは,簡単に言えばランダムということです。一般に,イベントがランダムに発生するとき,その回数はポアソン分布に従います。
超クリティカルな質問です。まず,ランダムというのを数学的に説明すると「起こる確率が常に一定である」となります。そして,もともとポアソン分布というのは二項分布の極限として与えられています。その極限のとり方は「生起確率を一定に保って」「試行数を無限大に飛ばす」というものです。この操作が,ポアソン分布がランダムなイベント発生の分布として利用されることの裏付けとなっています。
そして実は,無記憶なイベントの生起間隔は,指数分布に従うのです。ここの証明は少し長くなってしまうので,ポアソン分布同様省略させていただきます。
さて,残った話題はM/M/1モデルの結論である,式(1)の証明です。これは,微分方程式と三項間漸化式を解くことで求めることができます。詳しくは,以下の書籍をご覧ください。
ひとこと
とっつきにくい待ち行列理論ですが,M/M/1に注目して結論だけ見ると非常に面白いですよね。確率分布の性質を加味して数学的な処理を行なった結果,綺麗な式が出てくるということは驚きです。これは,分布の定式化や方程式の立て方の妥当性が示唆されているのではないかと思えます。
















ρ=2/3から「したがって,このタピオカ屋さんでは平均2/3
人分待たなければならないことが分かります。」とありますが、正しくはρ/(1-ρ)=(2/3)/(1-2/3)=2人分待たなければなりません。
ご指摘ありがとうございます。修正しました。