この記事では,研究のサーベイをまとめていきたいと思います。ただし,全ての論文が網羅されている訳ではありません。また,分かりやすいように多少意訳した部分もあります。ですので,参考程度におさめていただければ幸いです。
間違えている箇所がございましたらご指摘ください。随時更新予定です。他のサーベイまとめ記事はコチラのページをご覧ください。
本記事の内容
大学で学習した「情報セキュリティ」の内容を網羅的にまとめていくものです。目次は以下の記事をご覧ください。

暗号と認証の必要性
情報セキュリティ<概要編>でもお伝えした通り,情報セキュリティには3つの要件があります。
【情報セキュリティの3要件】
●機密性(Confidentiality)
●完全性(Integrity)
●可用性(Availability)
その中でも,暗号と認証は機密性を維持するための手法として知られています。機密性とは,アクセスを許可されたものだけが情報を手に入れられることを指します。
復習
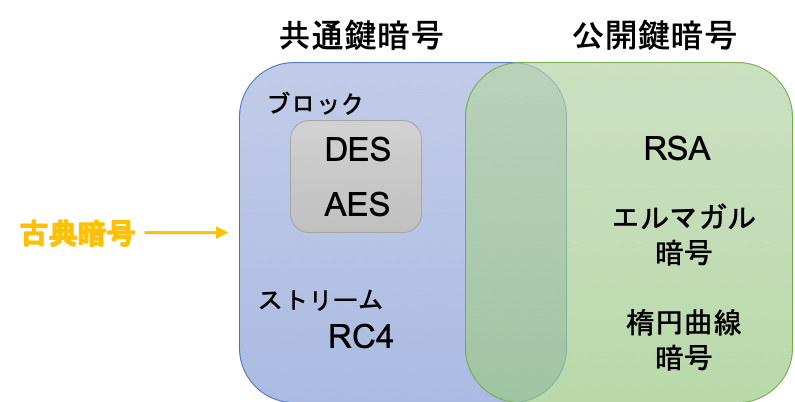 暗号の大別
暗号の大別古典暗号では,暗号化のアルゴリズムや暗号鍵は秘密にしておくというアイディアに基づいていました。一方,現代暗号は,暗号化のアルゴリズムを公開しつつも,お互いに共通鍵を何かしらの形で共有するというアイディアに基づきます。
暗号と複合に同一の鍵を利用する方式を,共通鍵暗号化方式と呼びます。処理が高速な一方で,共通鍵をどのように交換するのかが問題でした。一方,暗号化の鍵を公開しながら,複合化の鍵は秘密にしておくことで暗号化を実現する方式を,公開鍵暗号化方式と呼びます。
公開鍵暗号化方式の中でも代表的なアルゴリズムに,RSAが挙げられます。詳しくは,以下で解説しています。

ハッシュ関数
ハッシュ関数とは,「一方向性」「第2原像計算困難性」「衝突困難性」の特徴を有した関数のことを指します。
●一方向性
→出力から入力を推測できない
●第2原像計算困難性
→入力と出力が与えられた時に同じ出力を得る入力を推測できない
●衝突困難性
→同じ出力を得るような入力を推測できない
ハッシュ関数の特徴としては,固定長であることからデータ構造を分かりやすくすることができます。また,データ自体を短く表現することになるため,計算量を削減することも可能になります。このような特徴をもつハッシュ関数を,Diffie-Hellman鍵交換アルゴリズムと組み合わせることで,強力な鍵交換アルゴリズムを構築することが可能になります。
ハッシュ関数の利用
ハッシュ関数は,身近なものにも利用されています。例えば,Webサイトで登録するパスワードもサーバ内ではハッシュ値で保存されています。実際の応用でも,入力された文字列のハッシュ値と,保存されたハッシュ値を比較することで認証を行なっています。
他にも,ハッシュ関数は改ざんの検出にも利用されます。元のメッセージのハッシュ値を保存しておくことで,改ざんを検出したいメッセージのハッシュ値を比較することで改ざんの有無を調べることが可能になります。
実際には,メッセージの送信者が正当であることを証明するために,MAC(Message Authentication Code)が利用されます。すなわち,あらかじめ鍵を共有している相手であれば,その共有鍵をメッセージに付加すること,送信者としての正当性を証明できるのです。
デジタル署名
自分の秘密鍵で処理を行なった署名を付加させて,送信者の正当性を保証する手法をデジタル署名と呼びます。デジタル署名を施した人の公開鍵で署名に処理を施すことで,検知を行うことができます。太郎さんからメアリーさんにデジタル署名で通信を行う例を示してみます。
●太郎さん:秘密鍵で署名を作成
→「メッセージ+署名」
●メアリーさん:太郎さんの公開鍵で複合
→「メッセージ+複合された署名」
→メッセージ=複された署名であればOK
デジタル署名をRSAで行う場合は,暗号と複合の対称性から,以下のようにアルゴリズムを構築することができます。
●$M$:メッセージ
●$S$:署名
●$R$:検証結果
●$l_a$:送信者の秘密鍵
●$l_b$:送信者の公開鍵
●$m$:素数の積(送信者の公開鍵)
\begin{eqnarray}
R &=& S^{l_b}\ \rm{mod}\ m \\
S &=& M^{l_a}\ \rm{mod}\ m
\end{eqnarray}
暗号技術への攻撃
現代暗号では基本的にアルゴリズムが公開されていますので,秘密鍵を求めることが攻撃者の目的です。そして,情報セキュリティ<暗号と認証その1>でもお伝えしているように,アルゴリズムを公開するメリットは,攻撃に対して様々なテストを行える点にあります。現代暗号は,以下のような攻撃から耐えられたアルゴリズムが利用されています。
【現代暗号への攻撃テストの種類】
●暗号文単独攻撃
→暗号文のみ手に入る状況
●既知平文攻撃
→特定の平文と対応する暗号文が手に入る状況
●選択平文攻撃
→任意の平文と対応する暗号文が手に入る状況
●選択暗号文攻撃
→任意の暗号文と対応する平文が手に入る状況
また,暗号技術に対する代表的な攻撃は,以下が挙げられます。
●総当たり攻撃
→全ての組み合わせを試行
●辞書攻撃
→データベースを利用して総当たりを行う
●差分解読法
→入力の微小変化に対して出力の変化を調べる方法
安全性
安全性に関する概念は数多くありますが,代表的な例は以下の通りです。
●情報理論的安全性
何もない状態で平文を(あてずっぽうで) 推測するのと, 暗号文を見てから推測するのとで推測が当たる可能性が変わらない場合を情報理論的に安全であるという。ーシャノン(1949年)
●計算量的安全性
鍵長が$k$bitである場合,$2k$個の鍵を総当りすれば必ず解読できるので,$k$を大きく取って「実用上」解読を不可能にした状態。
●等価安全性($x$ビット安全性)
暗号技術に対して最も効率的な攻撃を行った際に,解読に必要となる計算量が 2xであること。
まとめ
情報セキュリティの暗号化についてお伝えしました。ハッシュ関数は,情報系の入門科目で必ず学習する用語ですが,今まではイマイチ実態を掴めていませんでした。Linux等では実際にハッシュ値を求めることができますので,実際に試してみると実感が湧いてきて楽しいですよ。