本シリーズでは,ディープラーニングを実装する際に強力な手助けをしてくれる「TensorFlow」についてです。公式チュートリアルを,初心者に向けてかみ砕きながら翻訳していこうと思います。(公式ページはこちらより)
今回はNo.5で,「正則化とドロップアウト」編です。その他の記事は,こちらの「TensorFlowの公式チュートリアルを初心者向けに読み解く」をご覧ください。
基本的な流れ
TensolFlowでディープラーニングを実装する流れは,以下のようになります。
●データセットの読み込み
●ネットワークの定義
●最適化アルゴリズムの定義
●学習の実行
●評価の実行
●予測の実行
必要なモジュール等の準備
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plttensorflowとkerasをインポートしましょう。計算用にnumpy,可視化用にseaborn, matplotlib.pyplotもインポートします。
データセットの読み込み
NUM_WORDS = 10000
(train_data, train_labels), (test_data, test_labels) = keras.datasets.imdb.load_data(num_words=NUM_WORDS)
def multi_hot_sequences(sequences, dimension):
results = np.zeros((len(sequences), dimension))
for i, word_indices in enumerate(sequences):
results[i, word_indices] = 1.0
return results
train_data = multi_hot_sequences(train_data, dimension=NUM_WORDS)
test_data = multi_hot_sequences(test_data, dimension=NUM_WORDS)今回は,映画のレビューに関するデータセットを利用します。テキスト解析編ではembedding層を追加して系列長を揃えました。ここでは,10000次元のマルチホットベクトルを作成して系列長を揃えていきます。つまり,各レビューを出現ランキング10000位以内の単語だけで表すということです。
試しに,作ったデータセットの概要を確認してみましょう。
plt.plot(train_data[0])
単語リストは出現ランキング順にソートされているので,インデックスが小さいほどたくさん出現している傾向が見て取れます。使われていない単語もたくさんありますね。
ネットワークの定義
baseline_model = keras.Sequential([
keras.layers.Dense(16, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
baseline_model.summary()今まで通りの流れです。比較対象として,過学習対策を何も施さないナチュラルなネットワークをbaselineとして定義します。
続いて,ユニットの数が少ないネットワークを定義します。
smaller_model = keras.Sequential([
keras.layers.Dense(4, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dense(4, activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
smaller_model.summary()
また,ユニット数が大きいモデルも準備します。
bigger_model = keras.models.Sequential([
keras.layers.Dense(512, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dense(512, activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
bigger_model.summary()
最適化アルゴリズムの定義
baseline_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
smaller_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
bigger_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
それぞれ,同じ条件で最適化させていきます。
学習の実行
baseline_history = baseline_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
smaller_history = smaller_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
bigger_history = bigger_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)学習も,比較のために同じ条件で行います。
評価の実行
def plot_history(histories, key='binary_crossentropy'):
plt.figure(figsize=(16,10))
for name, history in histories:
val = plt.plot(history.epoch, history.history['val_'+key],
'--', label=name.title()+' Val')
plt.plot(history.epoch, history.history[key], color=val[0].get_color(),
label=name.title()+' Train')
plt.xlabel('Epochs')
plt.ylabel(key.replace('_',' ').title())
plt.legend()
plt.xlim([0,max(history.epoch)])
plot_history([('baseline', baseline_history),
('smaller', smaller_history),
('bigger', bigger_history)])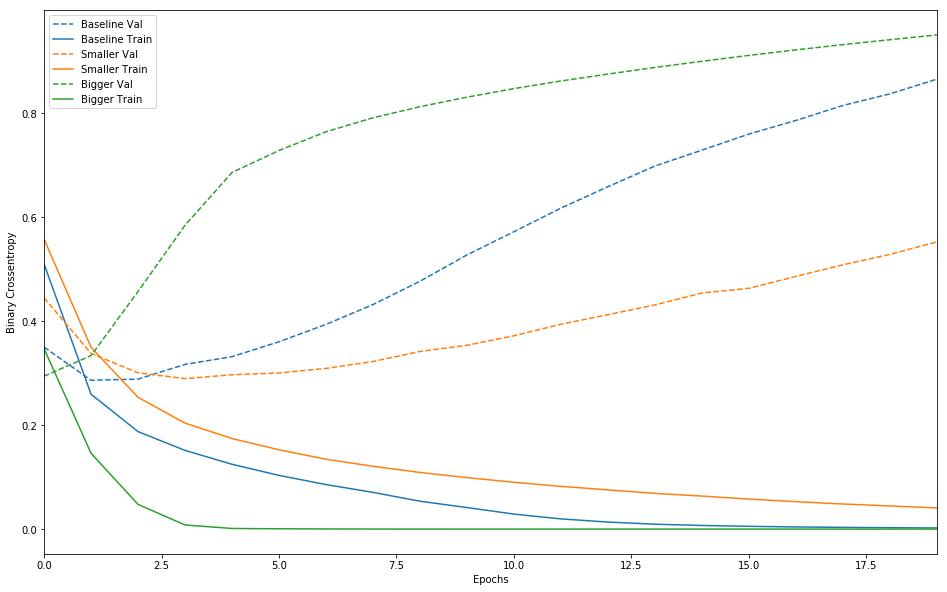
実線が訓練データに対する誤差関数(クロスエントロピー)の値,点線が評価データに対する誤差関数(クロスエントロピー)の値です。見てわかる通り,ユニット数が大きいネットワークほど過学習(誤差関数の値が大きい)していることが分かります。また,ユニット数が大きなネットワークは過学習のスピードも急激です。そこで,以下では過学習防止の策として「正則化」「ドロップアウト」を施していきます。
正則化
正則化とは,損失関数に重みパラメータに関する項を加えることで,重みパラメータの値が大きくなりすぎないように制限する手法です。加える項の種類によって,正則化は大きく分けて「L1正則化」と「L2正則化」に分けられます。
L1正則化は単純に重みパラメータの絶対値を足すというアイディア,L2正則化は重みパラメータのノルムの二乗を足すというアイディアです。L2正則化は,別名重み減衰とも呼ばれています。今回は,このL2正則化を施したネットワークも用意してみました。最適化と学習の条件等は,今までと同様です。
l2_model = keras.models.Sequential([
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
l2_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
l2_model_history = l2_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
こちらの正則化を施したモデルを,baselineのシンプルなネットワークと比較してみましょう。
plot_history([('baseline', baseline_history),
('l2', l2_model_history)])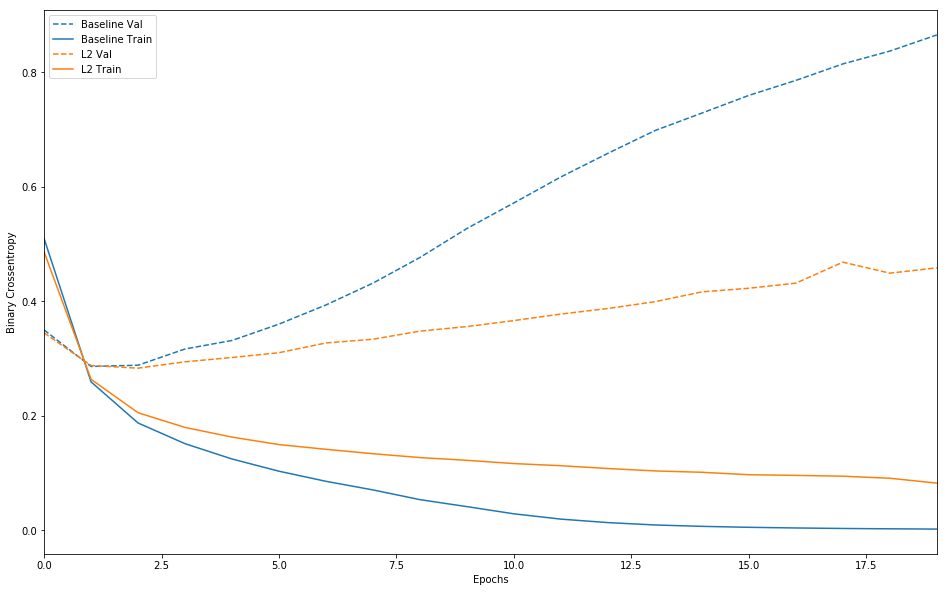
過学習が防止されている様子が分かります!
ドロップアウト
他にも,各層で出力される特徴量のうち,ある比率を0にすることで過学習を防止するというアイディアがあります。こちらは,訓練時に行うもので,テスト時にはドロップアウトを行う代わりに最後の出力をドロップアウトに従ってスケールダウンさせるという手法を取ります。
先ほどと同じように,新たにモデルを作成・学習・評価していきます。
dpt_model = keras.models.Sequential([
keras.layers.Dense(16, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dropout(rate=0.5),
keras.layers.Dense(16, activation=tf.nn.relu),
keras.layers.Dropout(rate=0.5),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
dpt_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
dpt_model_history = dpt_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)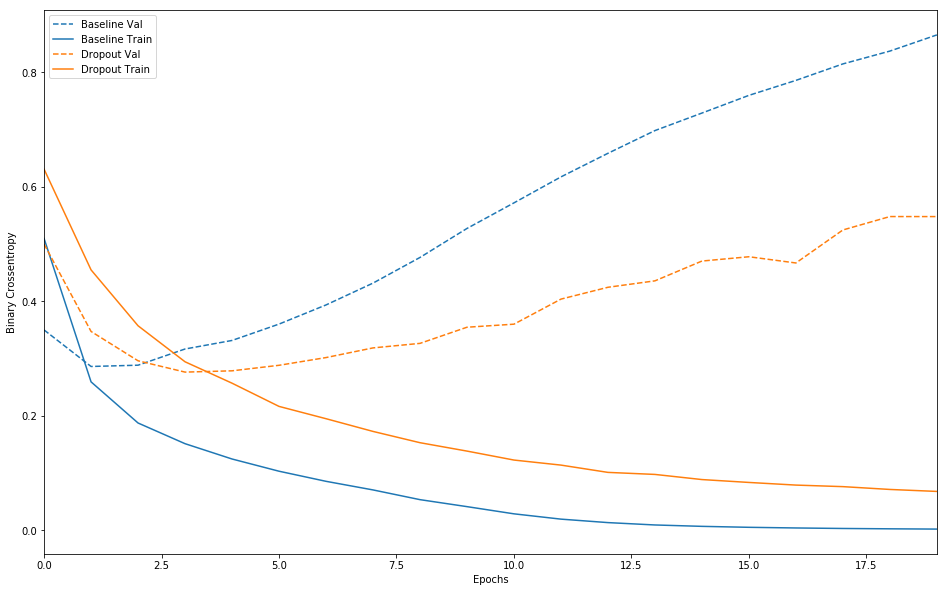
完全に過学習を抑えられているという訳ではありませんが,単純なネットワークに比べて改善が見られていることが分かります。
予測の実行
今回は行っていません。

















