この記事では,研究のサーベイをまとめていきたいと思います。ただし,全ての論文が網羅されている訳ではありません。また,分かりやすいように多少意訳した部分もあります。ですので,参考程度におさめていただければ幸いです。間違えている箇所がございましたらご指摘ください。随時更新予定です。
音源分離とは
音源分離とは,音響メディアを対象とした信号処理技術の1つです。カクテルパーティー効果として知られているように,人間の耳も複数の音を聞き分けられます。機械に対しても,人間と同じように音を聞き分けさせたいというのが音源分離の考えになります。音源分離ができることで,以下のような分野への応用が考えられます。
●雑音抑制
●音声認識
●自動採譜
●作曲システム
●補聴器
…
音を機械に認識させるための第一歩が音源分離なのです。
位置づけ
音源分離は単独のタスクではなく,いくつか付随する問題があります。
【音源分離に付属する問題】
●音源定位
●音源追跡
音源分離と音源位置は「卵が先か鶏が先か」の関係になっています。つまり,位置が分かれば分離は簡単,分離ができれば定位は簡単という関係です。
前提
分類に入る前に,音源分離においてよく使われる前提条件に関して確認していきたいと思います。
【よく利用される条件】
●定常雑音仮定
→ノイズの統計的性質が時間に依らず一定
●センサの有無
→空間情報など
●マイク数と音源数
→大小によって手法が異なる
●事前情報
ーユーザーアノテーション
ー音色情報
ー楽譜情報
…
これらの条件によって,分類の場合分けをしていきます。
分類
【音源分離】
●モノラルチャネル音源分離
・教師あり(①)
・教師なし(②)
●マルチチャネル音源分離
・劣決定条件(音源数>マイク数)
ー教師あり(③)
ー教師なし(④)
・優決定条件(音源数≦マイク数)
ー教師あり(⑤)
・教師なし(⑥)
【よく使われる手法】
①NMF
②NMF+クラスタリング
③NMF/深層学習
④SC+方位クラスタリング
⑤ビームフォーマ
⑥ICA/IVA
このように音源分離を分類することができました。また,音源定位と音源追跡に関しては以下の手法がよく使われます。
●音源定位
→MUSIC法
●音源追跡
→カルマンフィルタ
→パーティクルフィルタ
アプローチ
音源分離の基本的なアプローチ方法を考えていきます。北村先生のアイディアを基にすると,以下の流れになります。
【音源分離のアプローチ】
A.モデル化の対象選択
B.モデル化の実行
C.数値解析
A.モデル化の対象
●音色(周波数)
●時間
●空間
モデル化の対象は,上記の特徴量となります。多くの手法では,音色と時間を組み合わせた「スペクトログラム」を利用しています。また,スペクトログラムに空間情報を付け加えてICAやIVAとしてモデル化する場合もあります。
 スペクトログラム抽出の流れ
スペクトログラム抽出の流れ
B.モデル化の実行
●統計モデル
●物理モデル
●回路モデル
選択された対象は上記の3種類にモデル化されます。統計モデルはNMFやICAが挙げられます。音源の統計的な性質に注目してモデル化する手法です。物理モデルはビームフォーマが挙げられます。音源の空間伝達の現象に注目してモデル化する方法です。回路モデルはニューラルネットワークが挙げられます。特徴量抽出によるクラスタリングを用いる方法です。
C.数値解析
実際の解法は
それぞれのモデルに対応して
異なります。
●統計モデル
→最尤推定/ベイズ推定
●物理モデル
→最急降下法/ニュートン法
●回路モデル
→誤差逆伝播法/確率的勾配法
注目すべき特徴量
音源分離は,音源がもつ特徴に従ってパラメータを設定することが多いです。
【注目すべき特徴】
●スパース性
→アクティブな成分は一部だけ
●低ランク性
→音楽は繰り返し構造が多い
●連続性
→音声などは連続的に変化する
モノラルチャネル音源分離
モノラルチャネルの音源分離に対しては,以下の2つの手法が用いられてきました。
【モノラル音源分析】
①計算論的聴覚情景分析
②スパース・低ランクモデル化
①は,人間の聴覚機能を計算機で実現しようとするアプローチです。時間領域に注目した調波時間構造化クラスタリングが提案されています。②では,「スパース性」「低ランク性」をよく表せるモデルとしてNMF(非負値行列因子分解)を採用します。最近では,NMFの応用幅の広さから②のアプローチをとられる方が多いです。
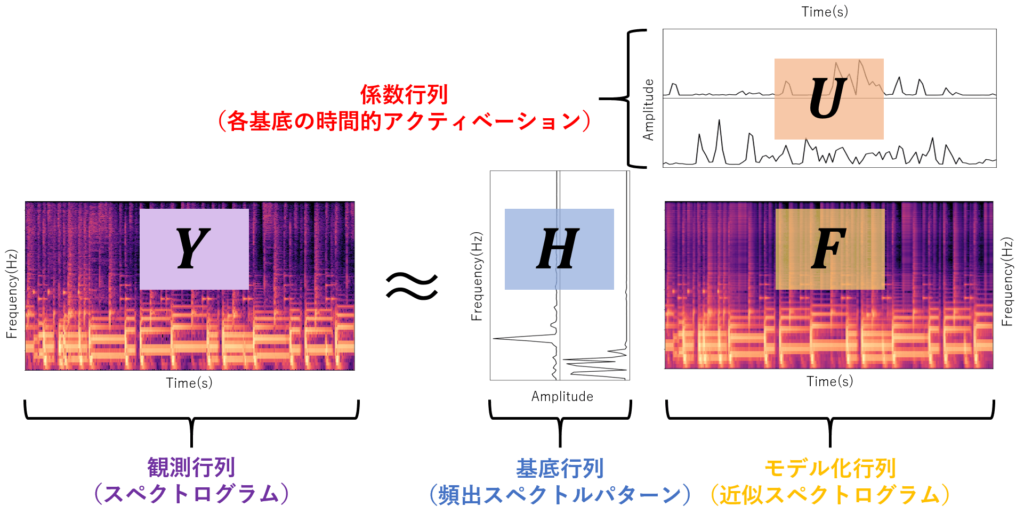 NMFの音源分離への応用
NMFの音源分離への応用また,モノラルチャネル音源分離では事前に得られる情報が少ないため,教師ありでモデル化していくことが多いです。以下に,複素NMFを利用した教師あり音源分離の概念図を示します。
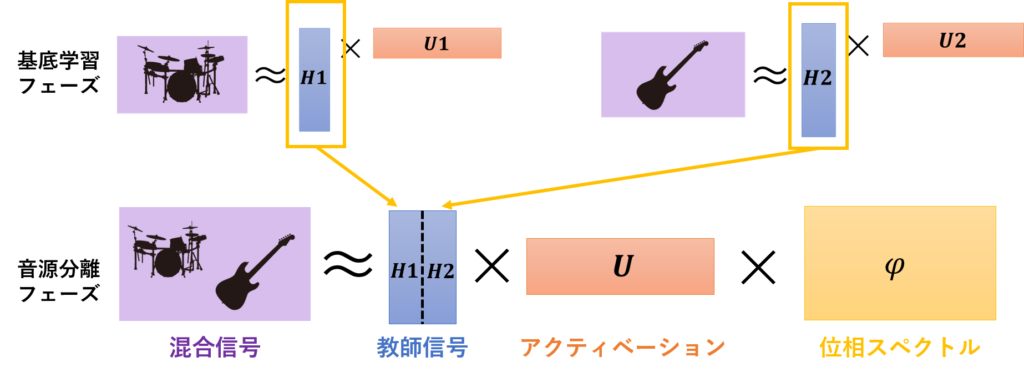 教師あり学習(複素NMFの場合)
教師あり学習(複素NMFの場合)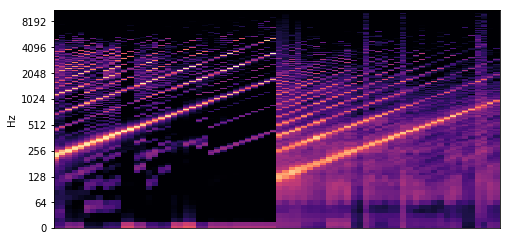 教師基底行列の例
教師基底行列の例
NMFの弱点
【NMFの弱点】
●解に一意性がない
●初期値に依存する
●局所解にも収束する
●基底数の推定が明確でない
しかし,NMFには上記のような弱点が指摘されています。これらの弱点に立ち向かうため,様々な形のNMFが考案されています。
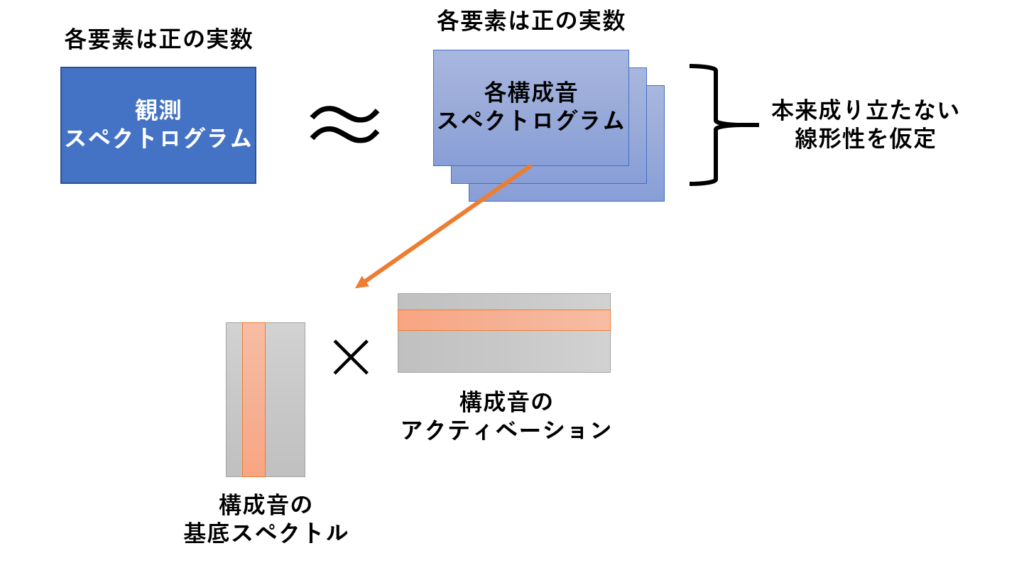 NMFが仮定する加法性
NMFが仮定する加法性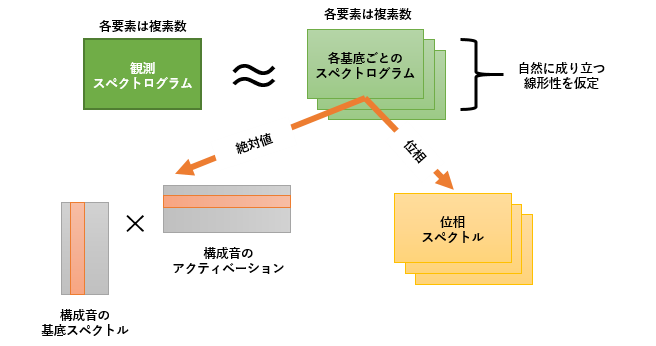 複素NMFが仮定する加法性
複素NMFが仮定する加法性
様々なNMF
【初期値の設定方法】
●混合ガウス分布
●特異値分解
●クラスタリング法
●相関情報
【教師情報の活用】
●楽譜情報
●音色情報
【制約を付ける】
●直交化制約
●スパース制約
●凸最適化制約
●未相関制約
●シフト不変制約
●基底一部固定制約
【特徴量の利用】
●MFCC特徴量クラスタリング
●スペクトル包絡保存
●音量ダイナミクス
●調波・非調波統合モデル
【新モデル】
●基底変形型
●基底学習型
●基底生成型
●複素型
●視聴覚統合型
●重畳マルコフ連鎖モデル
●全極スペクトルモデル
●演奏意図関数
【確率モデル】
●調波パラメトリック
●ノンパラメトリックベイズ
●無限潜在的調波配分法
最新の動向
最新の手法は,統計的手法と多次元への拡張の2つに分類できます。
【最新の動向】
●NMF(モノラル)
→CTF(相関テンソル分解)
→ILRTA(独立低ランクテンソル分析)
●MNMF(マルチ)
→ICA(独立成分分析)
→IVA(独立ベクトル分析)
→ILRMA(独立低ランク行列分析)
まとめ
私の興味関心は
●モノラルチャネル音源分離
●音色・時間を対象
●統計モデル
●制約付きNMF
になっています。これからも精進していきます。
●「音源分離における音響モデリング」(北村,2017,日本音響学会 サマーセミナー 招待講演)
●「スパース表現と凸最適化に基づく非負値行列因子分解と音楽信号処理への応用」(湯川,2017,TELECOM FRONTIER)
●「全極スペクトルモデルを用いた調波時間因子分解による多重音解析」(中村/亀岡,2015,情報処理学会)















