本シリーズでは,ディープラーニングを実装する際に強力な手助けをしてくれる「TensorFlow」についてです。公式チュートリアルを,初心者に向けてかみ砕きながら翻訳していこうと思います。(公式ページはこちらより)
今回はNo.4で,「回帰」編です。その他の記事は,こちらの「TensorFlowの公式チュートリアルを初心者向けに読み解く」をご覧ください。
基本的な流れ
TensolFlowでディープラーニングを実装する流れは,以下のようになります。
●データセットの読み込み
●ネットワークの定義
●最適化アルゴリズムの定義
●学習の実行
●評価の実行
●予測の実行
必要なモジュール等の準備
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layerstensorflowとkerasをインポートしましょう。計算用にnumpy,可視化用にseaborn, matplotlib.pyplotもインポートします。
データセットの読み込み
dataset_path = keras.utils.get_file("auto-mpg.data", "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values = "?", comment='\t',
sep=" ", skipinitialspace=True)今回は,車の燃費に関するデータセットを利用します。アメリカの燃費の単位は「Mile per gallon」を利用するため,MPGと呼ばれています。二行目では,列名を付けてしまっています。三行目では,データセットを利用しやすい形に整形しています。例えば,欠陥値は”?”を指定し,タブを使ったコメントは削除し,データ区切りは半角スペースと指定しています。skipinitialspaceでは,コンマの後のスペースを無視する設定にしています。
データセットの概要を確認しましょう。
dataset = raw_dataset.copy()
dataset.tail() MPG Cylinders Displacement Horsepower Weight Acceleration Model Year Origin
393 27.0 4 140.0 86.0 2790.0 15.6 82 1
394 44.0 4 97.0 52.0 2130.0 24.6 82 2
395 32.0 4 135.0 84.0 2295.0 11.6 82 1
396 28.0 4 120.0 79.0 2625.0 18.6 82 1
397 31.0 4 119.0 82.0 2720.0 19.4 82 1
欠損値を確認してみます。
dataset.isna().sum()MPG 0
Cylinders 0
Displacement 0
Horsepower 6
Weight 0
Acceleration 0
Model Year 0
Origin 0
dtype: int64どうやら,Horsepowerの列にNaNが含まれているようなので,今回は簡単のために削除してしまいます。
dataset = dataset.dropna()
また,Originの列は扱いやすいone-hot-vector形式に変換しておきましょう。
origin = dataset.pop('Origin')
dataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
dataset.tail()MPG Cylinders Displacement Horsepower Weight Acceleration Model Year USA Europe Japan
393 27.0 4 140.0 86.0 2790.0 15.6 82 1.0 0.0 0.0
394 44.0 4 97.0 52.0 2130.0 24.6 82 0.0 1.0 0.0
395 32.0 4 135.0 84.0 2295.0 11.6 82 1.0 0.0 0.0
396 28.0 4 120.0 79.0 2625.0 18.6 82 1.0 0.0 0.0
397 31.0 4 119.0 82.0 2720.0 19.4 82 1.0 0.0 0.0
そして,データセットを訓練用と評価用に分割します。今回は燃費の回帰なので,MPGのラベルはPOP(削除)しておきます。
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
訓練用データを可視化していきましょう。
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")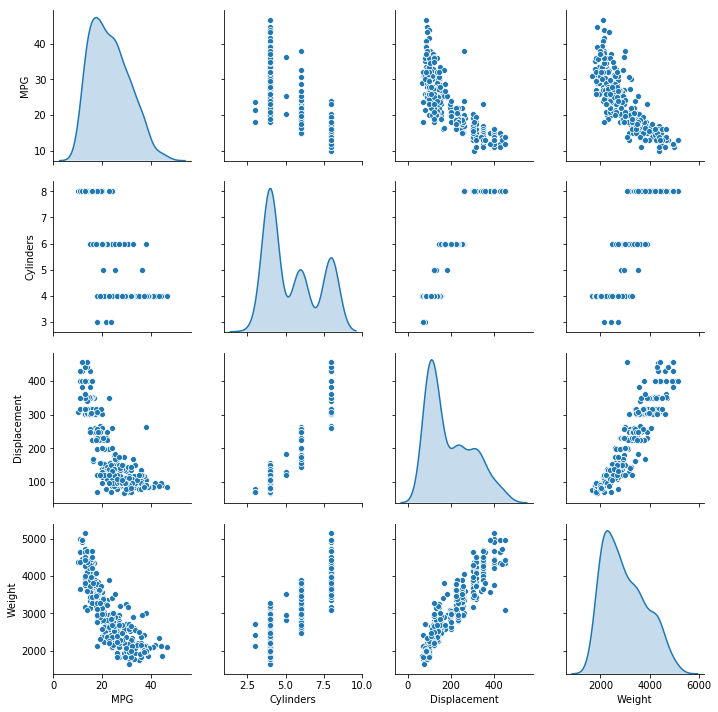
各種統計値も確認してみます。
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats count mean std min 25% 50% 75% max
Cylinders 314.0 5.477707 1.699788 3.0 4.00 4.0 8.00 8.0
Displacement 314.0 195.318471 104.331589 68.0 105.50 151.0 265.75 455.0
Horsepower 314.0 104.869427 38.096214 46.0 76.25 94.5 128.00 225.0
Weight 314.0 2990.251592 843.898596 1649.0 2256.50 2822.5 3608.00 5140.0
Acceleration 314.0 15.559236 2.789230 8.0 13.80 15.5 17.20 24.8
Model Year 314.0 75.898089 3.675642 70.0 73.00 76.0 79.00 82.0
USA 314.0 0.624204 0.485101 0.0 0.00 1.0 1.00 1.0
Europe 314.0 0.178344 0.383413 0.0 0.00 0.0 0.00 1.0
Japan 314.0 0.197452 0.398712 0.0 0.00 0.0 0.00 1.0
ここで,正規化(機械学習の前処理)されていない特徴量は,あらかじめ正規化しておく必要があります。正規化は,入力の単位に訓練が依存することを防ぐために行われます。
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
ネットワークの定義
def build_model():
model = keras.Sequential([
layers.Dense(64, activation=tf.nn.relu, input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation=tf.nn.relu),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=['mean_absolute_error', 'mean_squared_error'])
return model
model = build_model()
model.summary()Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 64) 640
_________________________________________________________________
dense_1 (Dense) (None, 64) 4160
_________________________________________________________________
dense_2 (Dense) (None, 1) 65
=================================================================
Total params: 4,865
Trainable params: 4,865
Non-trainable params: 0
_________________________________________________________________今回は,汎用性のある方法としてbuild_modelという関数を定義しています。今まで通り,summaryメソッドで概要を確認します。
このモデルを小さいデータで試しに動かしてみます。
example_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_resultarray([[ 0.30137864],
[ 0.02479791],
[-0.14193764],
[ 0.08205271],
[ 0.4449516 ],
[ 0.13355428],
[ 0.49014974],
[ 0.48400852],
[ 0.06517904],
[ 0.5086561 ]], dtype=float32)しっかりとpredictメソッドで予測ができていることが分かります。
最適化アルゴリズムの定義
build_model関数の中で定めてしまっています。
学習の実行
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print('')
print('.', end='')
EPOCHS = 1000
history = model.fit(
normed_train_data, train_labels,
epochs=EPOCHS, validation_split = 0.2, verbose=0,
callbacks=[PrintDot()])
さて,実際にモデルを学習させていきましょう。今回は,進捗度合いをドットで表すクラス「PrintDot」を定義してから学習させていきます。historyという変数に代入することで,以下のように学習過程を定量的に表示し,かつ視覚化することができます。
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_history(history):
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [MPG]')
plt.plot(hist['epoch'], hist['mean_absolute_error'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mean_absolute_error'],
label = 'Val Error')
plt.legend()
plt.ylim([0,5])
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Square Error [$MPG^2$]')
plt.plot(hist['epoch'], hist['mean_squared_error'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mean_squared_error'],
label = 'Val Error')
plt.legend()
plt.ylim([0,20])
plot_history(history)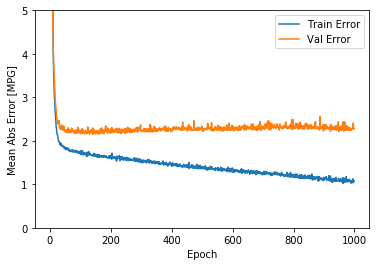
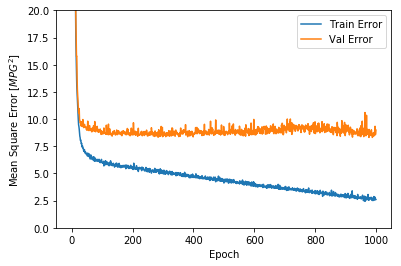
この結果を見ると,100Epoch程度を境目にエラーが減少しなくなっている傾向が見られます。そこで,モデルが改善しなくなれば学習を止めるようにパラメータを指定します。過学習の防止というやつです。fitメソッドのコールバック引数にkerasのEarlystoppingで生成したインスタンスを指定します。
model = build_model()
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])
plot_history(history)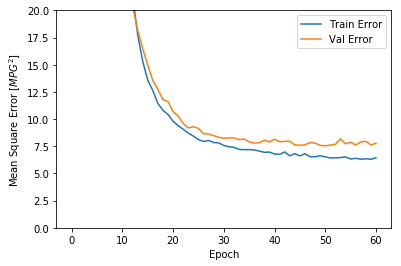

評価の実行
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=0)
print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))
Testing set Mean Abs Error: 1.95 MPG回帰の誤差なので,平均絶対誤差を利用しました。
予測の実行
test_predictions = model.predict(normed_test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])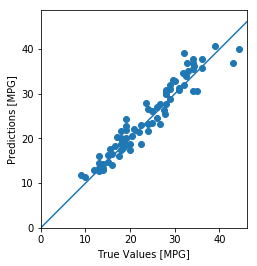
予測の誤差を見てみると,このようになります。
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
平均二乗誤差基準で回帰を行っているため,本来であれば誤差はガウス分布に従うはずです。しかし,今回は(心の目で見ればガウス分布ですが)ガウス分布とは少し異なる分布が得られました。これは,サンプル数が少ないからだと考えられる,とチュートリアルでは説明されていました。
















