【超初心者向け】線形回帰モデルをpythonで分かりやすく実装してみた。Beginaid

線形回帰を実装したいけど…

何から手を付けていいのか分からねえや…

今回は，scikit-learnなどの既成ライブラリに頼らずに線形回帰モデルを実装していこうと思います。また，本記事はpython実践講座シリーズの内容になります。その他の記事は，こちらの「Python入門講座/実践講座まとめ」をご覧ください。

コーディングに関して未熟な部分がたくさんあると思いますので，もし何かお気づきの方は教えていただけると幸いです。また，誤りについてもご指摘していただけると非常に助かります。

理論

線形回帰モデルの理論は，こちらの記事をご覧ください。基本的に，本記事では数式を示しません。

【サーベイまとめ】線形回帰とは？基底関数を中心として出来るだけ分かりやすく簡潔に説明します。この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多...

データセット

今回用いるデータセットは，scikit-learnが提供しているものを利用します。scikit-learnは主に「回帰用」「分類用」の２種類のデータセットを提供していますが，今回はその中で「回帰用」に当たる「ボストンの住宅価格」に関するデータを利用していきます。

レコード(行)数	506
カラム(列)数	14
用途	回帰
URL	scikit-learn公式サイト

CRIM	人口 1 人当たりの犯罪発生数
ZN	25,000 平方フィート以上の住居区画の占める割合
INDUS	小売業以外の商業が占める面積の割合
CHAS	チャールズ川によるダミー変数 (1: 川の周辺, 0: それ以外)
NOX	NOx の濃度
RM	住居の平均部屋数
AGE	1940 年より前に建てられた物件の割合
DIS	5 つのボストン市の雇用施設からの距離 (重み付け済)
RAD	環状高速道路へのアクセスしやすさ
TAX	$10,000 ドルあたりの不動産税率の総計
PTRATIO	町毎の児童と教師の比率
B	町毎の黒人 (Bk) の比率を次の式で表したもの。 1000(Bk – 0.63)^2
LSTAT	給与の低い職業に従事する人口の割合 (%)

コード

最初に，コードを部分的に解説していった後に，全体のコードをお伝えしていこうと思います。

必要なライブラリのインポート

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from pandas import DataFrame
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

まずは，必要なライブラリをインポートしましょう。scikit-learnなどの既成ライブラリに頼らずに線形回帰モデルを実装したいのですが，モデル評価指標の計算のために「mean_squared_error」と「r2_score」もインポートしています。

データフレームの作成

boston = datasets.load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target
df.head()

説明変数間の相関を確認

sns.pairplot(df)

各説明変数の関係について視覚的に確認します。この中でも，特に強い正の相関を持っている「RM」を説明変数として１つ選び，目的変数「PRICE」に対して線形回帰を行っていきましょう。

RMとPRICEの確認

sns.pairplot(df[['RM', 'PRICE']])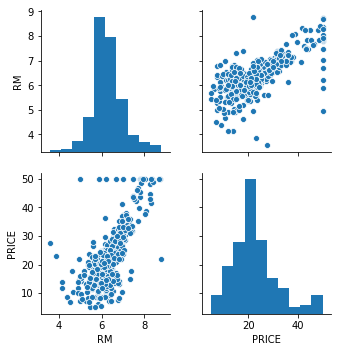

先ほどの全変数に対しての相関関係を見るのではなく，RMとPRICEにのみ注目したグラフを確認します。

基底関数の定義

def Polynomial(x, M):
  phi_x = np.array([x**(j) for j in range(M+1)]).T
  return phi_x

def Gaussian(X):
  D = X.shape[0]
  N = X.shape[1]
  mu = np.array([[np.mean(X[j,:]) for j in range(D)]]).T
  s = np.array([[np.sqrt(np.var(X[j, :])) for j in range(D)]]).T
  phi_x = np.array(np.e**(-(X - mu)**2 / (2*s**2))).T
  return [phi_x, mu, s]

def Sigmoid(X):
  D = X.shape[0]
  N = X.shape[1]
  mu = np.array([[np.mean(X[j,:]) for j in range(D)]]).T
  s = np.array([[np.sqrt(np.var(X[j, :])) for j in range(D)]]).T
  a = (X - mu) / s 
  phi_x = 1/(1+np.e**(-a)).T
  return [phi_x, mu, s]

上から，多項式基底，ガウス基底，シグモイド基底になります。特に，多項式基底において$M=1$と設定すると，単項式回帰になります。すべての基底関数の出力は縦ベクトルで表し，ガウス基底とシグモイド基底の平均と標準偏差は，入力行列の「説明変数のサンプル数方向」に対して，それぞれ計算したものを利用します。ですので，平均と標準偏差は入力行列の「説明変数の種類」の数だけ生成されることになり，基底関数の数と一致します。

計画行列作成

def DesignMatrix(phi_X):
  N = phi_X.shape[0]
  phi_ones = np.ones(N).T
  design_matrix = np.c_[phi_ones, phi_X]
  return design_matrix

計画行列を作成するための関数です。基底関数$\phi_0$は$1$と定めていますので，phi_onesというベクトルを，基底関数の出力の左側にくっつけています。

重みパラメータの最適化

def OptimalWeight(design_matrix, t):
  optimal_weight = (np.linalg.inv(design_matrix.T @ design_matrix) @ (design_matrix.T)) @ t.T
  return optimal_weight

重みパラメータを最適化します。上でもとめた計画行列と，目的変数を引数として最適化された重みパラメータを返します。

モデルの出力

def Model(weight, phi_x):
  y_out = weight.T @ phi_x
  return y_out

関数定義するまでもありませんが，入力に基底関数を施したもの（phi_x）と最適化された重みパラメータの内積が線形回帰モデルの出力となります。

データセットの分割

x_train, x_test, y_train, y_test = train_test_split(boston.data[:, [5]], boston.target, random_state=0)
x_train = x_train.T
x_test = x_test.T
y_train = y_train.T
y_test = y_test.T
x_train_poly = x_train.flatten()
x_test_poly = x_test.flatten()

ボストンデータのRMに相当する列のみ取ってきます。そして，インポートしておいたsklearnのライブラリを利用して，ボストンデータを「75%の訓練（モデル学習用）データ」と「25%のテスト（モデル評価用）データ」に分割します。それぞれ，あとで都合がよいように転置を取って修正しています。また，多項式モデルでは入力が一次元として関数を定義していたので，そのように修正します。

モデルの学習

phi_X_poly1 = Polynomial(x_train_poly, 1)
phi_X_poly2 = Polynomial(x_train_poly, 2)
phi_X_poly3 = Polynomial(x_train_poly, 3)
phi_X_gauss = Gaussian(x_train)[0]
phi_X_sigm = Sigmoid(x_train)[0]

DM_poly1 = phi_X_poly1
DM_poly2 = phi_X_poly2
DM_poly3 = phi_X_poly3
DM_gauss = DesignMatrix(phi_X_gauss)
DM_sigm = DesignMatrix(phi_X_sigm)

w_opt_poly1 = OptimalWeight(DM_poly1, y_train)
w_opt_poly2 = OptimalWeight(DM_poly2, y_train)
w_opt_poly3 = OptimalWeight(DM_poly3, y_train)
w_opt_gauss = OptimalWeight(DM_gauss, y_train)
w_opt_sigm = OptimalWeight(DM_sigm, y_train)

モデルを学習させます（＝最適な重みパラメータを求めます）。今回は，多項式基底として$M=1,2,3$を利用しました。

モデルのテスト出力

phi_X_poly1_test = Polynomial(x_test_poly, 1)
phi_X_poly2_test = Polynomial(x_test_poly, 2)
phi_X_poly3_test = Polynomial(x_test_poly, 3)
phi_X_gauss_test = Gaussian(x_test)[0]
phi_X_sigm_test = Sigmoid(x_test)[0]

DM_poly1_test = phi_X_poly1_test
DM_poly2_test = phi_X_poly2_test
DM_poly3_test = phi_X_poly3_test
DM_gauss_test = DesignMatrix(phi_X_gauss_test)
DM_sigm_test = DesignMatrix(phi_X_sigm_test)

N_test = DM_poly1_test.shape[0]
y_poly1_test= np.array([Model(w_opt_poly1, DM_poly1_test[n,:]) for n in range(N_test)])
y_poly2_test= np.array([Model(w_opt_poly2, DM_poly2_test[n,:]) for n in range(N_test)])
y_poly3_test= np.array([Model(w_opt_poly3, DM_poly3_test[n,:]) for n in range(N_test)])
y_gauss_test = np.array([Model(w_opt_gauss, DM_gauss_test[n,:]) for n in range(N_test)])
y_sigm_test = np.array([Model(w_opt_sigm, DM_sigm_test[n,:]) for n in range(N_test)])

訓練データを使って求めた最適な重みパラメータを利用して，テストデータから出力を求めます。

定量評価

mse_poly1 = mean_squared_error(y_poly1_test, y_test)
mse_poly2 = mean_squared_error(y_poly2_test, y_test)
mse_poly3 = mean_squared_error(y_poly3_test, y_test)
mse_gauss = mean_squared_error(y_gauss_test, y_test)
mse_sigm = mean_squared_error(y_sigm_test, y_test)

R2_poly1 = r2_score(y_poly1_test, y_test)
R2_poly2 = r2_score(y_poly2_test, y_test)
R2_poly3 = r2_score(y_poly3_test, y_test)
R2_gauss = r2_score(y_gauss_test, y_test)
R2_sigm = r2_score(y_sigm_test, y_test)

print('MSE_poly1 = ', mse_poly1)
print('MSE_poly2 = ', mse_poly2)
print('MSE_poly3 = ', mse_poly3)
print('MSE_gauss = ', mse_gauss)
print('MSE_sigm = ', mse_sigm)

print('R2_poly1 = ', R2_poly1)
print('R2_poly2 = ', R2_poly2)
print('R2_poly3 = ', R2_poly3)
print('R2_gauss = ', R2_gauss)
print('R2_sigm = ', R2_sigm)

（以下は出力）
MSE_poly1 = 43.472041677202384
MSE_poly2 = 37.036872974321206
MSE_poly3 = 37.10046358044306
MSE_gauss = 72.13041721148669
MSE_sigm = 44.57442711949657

R2_poly1 = 0.04098622450766021
R2_poly2 = 0.27465819833584015
R2_poly3 = 0.22108417575897132
R2_gauss = -3.7688238397468767
R2_sigm = -0.1897487972972376

求めたテストデータからの最適な出力と（推定結果），テストデータの目的変数（元から持っているデータ）を照らし合わせて，定量的な指標を計算します。今回は，平均二乗誤差（MSE）と決定係数（R^2）を利用しました。

既成のライブラリによる評価

from sklearn import linear_model

clf = linear_model.LinearRegression()
clf.fit(x_train.T, y_train.T)
pred = clf.predict(x_test.T)
mse = mean_squared_error(y_test.flatten(), pred)
R2 = clf.score(x_test.T, y_test.T)

print('mse = ', mse)
print('R^2 = ', R2)

（以下は出力）
mse = 43.472041677202206
R^2 = 0.46790005431367815

sklearnに入っている既成のライブラリを利用して線形回帰をしてみました。自作のモデルとの比較で利用できそうです。

視覚的な評価

xlist = np.arange(np.min(x_train), np.max(x_train), 0.01)
Xlist = np.array([xlist])
ylist_poly1 = [Model(w_opt_poly1, Polynomial(x, 1)) for x in xlist]
ylist_poly2 = [Model(w_opt_poly2, Polynomial(x, 2)) for x in xlist]
ylist_poly3 = [Model(w_opt_poly3, Polynomial(x, 3)) for x in xlist]

DM_gauss_graph = DesignMatrix(Gaussian(Xlist)[0])
DM_sigm_graph = DesignMatrix(Sigmoid(Xlist)[0])

N_graph = DM_gauss_graph.shape[0]
ylist_gauss = np.array([Model(w_opt_gauss, DM_gauss_graph[n,:]) for n in range(N_graph)])
ylist_sigm = np.array([Model(w_opt_sigm, DM_sigm_graph[n,:]) for n in range(N_graph)])

グラフを描くための準備をしています。自分もハマってしまったのですが，ここでxlistとして生のボストンデータを利用するとカクカクな折れ線グラフが出力されます。それでは，モデルの妥当性を視覚的に確認することができないので，xlistとして「説明変数の最小値から最大値までを0.01の間隔でサンプリングしていった」リストを用意しました。間隔は適当に定めてOKですが，あまりにも大きいとカクカクしてしまうので注意が必要です。

plt.plot(xlist, ylist_poly1)
plt.plot(x_train_poly, y_train, 'o')
plt.show()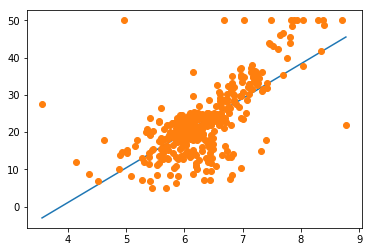

plt.plot(xlist, ylist_poly2)
plt.plot(x_train_poly, y_train, 'o')
plt.show()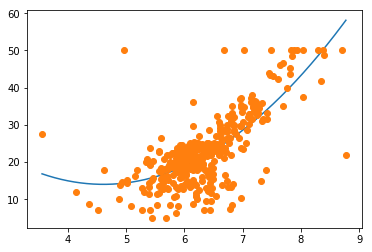

plt.plot(xlist, ylist_poly3)
plt.plot(x_train_poly, y_train, 'o')
plt.show()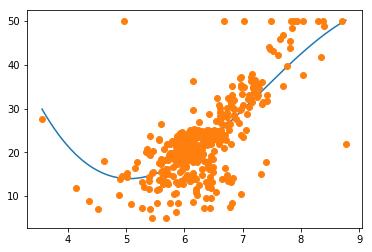

plt.plot(xlist, ylist_gauss)
plt.plot(x_train_poly, y_train, 'o')
plt.show()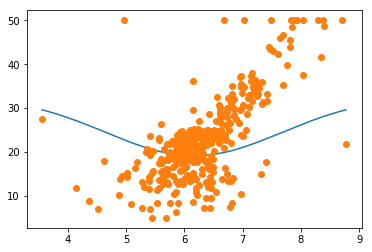

ガウス分布の形をしています。

plt.plot(xlist, ylist_sigm)
plt.plot(x_train_poly, y_train, 'o')
plt.show()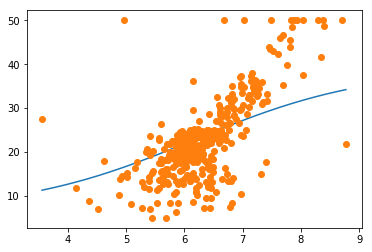

シグモイド関数の形をしています。

plt.plot(xlist, clf.predict(np.array([xlist]).T))
plt.plot(x_train_poly, y_train, 'o')
plt.show()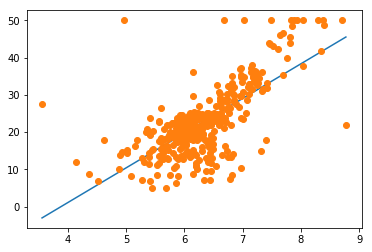

考察

今回は，ボストンデータの中から「RM（部屋数）」と「PRICE（価格）」の関係について注目しました。基底関数が多項式関数の場合，もちろん基底関数を増やすにしたがって滑らかなモデルが生成されますが，MSEとR^2を見てみると，多項式の次数が2の場合が最も定量的に良い結果が出ていることが分かります。

視覚的な確認により，多項式基底で$M=3$とした場合は，外れ値に敏感すぎる傾向にあることが分かります。明らかに，左側にポツンとある点に引きずられてしまっています。

また，既成のライブラリと比べて，今回のモデルの結果は芳しくありませんでした。理由としては，ガウス基底とシグモイド基底の個数が1つだったことが考えられます。今回の定義では，説明変数の個数とガウス基底とシグモイド基底の個数が一致するため，多くの説明変数を利用する重回帰分析になればなるほど，ガウス基底とシグモイド基底の威力が発揮されると思います。

ガウス基底とシグモイド基底で単回帰分析に対応するためには，基底の個数を固定してしまう（9個，など）という方法が考えられます。そうすることで，より妥当なモデルを構築することが可能になると考えられます。

もし理論にモヤモヤがあれば

機械学習スタートアップシリーズ　ベイズ推論による機械学習入門（KS情報科学専門書） [ 須山敦志 ]

¥3,080
(2024/11/21 14:35:16時点楽天市場調べ-詳細)

こちらの参考書は，誰もが挫折しかけるPRMLよりも平易に機械学習全般の手法について解説しています。おすすめの１冊になりますので，ぜひお手に取って確認してみてください。

全コード

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from pandas import DataFrame
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

boston = datasets.load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target
df.head()

sns_plot = sns.pairplot(df)

def Polynomial(x, M):
  phi_x = np.array([x**(j) for j in range(M+1)]).T
  return phi_x

def Gaussian(X):
  D = X.shape[0]
  N = X.shape
  mu = np.array([[np.mean(X[j,:]) for j in range(D)]]).T
  s = np.array([[np.sqrt(np.var(X[j, :])) for j in range(D)]]).T
  phi_x = np.array(np.e**(-(X - mu)**2 / (2*s**2))).T
  return [phi_x, mu, s]

def Sigmoid(X):
  D = X.shape[0]
  N = X.shape
  mu = np.array([[np.mean(X[j,:]) for j in range(D)]]).T
  s = np.array([[np.sqrt(np.var(X[j, :])) for j in range(D)]]).T
  a = (X - mu) / s 
  phi_x = 1/(1+np.e**(-a)).T
  return [phi_x, mu, s]

def DesignMatrix(phi_X):
  N = phi_X.shape[0]
  phi_ones = np.ones(N).T
  design_matrix = np.c_[phi_ones, phi_X]
  return design_matrix

def OptimalWeight(design_matrix, t):
  optimal_weight = (np.linalg.inv(design_matrix.T @ design_matrix) @ (design_matrix.T)) @ t.T
  return optimal_weight

def Model(weight, phi_x):
  y_out = weight.T @ phi_x
  return y_out

x_train, x_test, y_train, y_test = train_test_split(boston.data[:, [5]], boston.target, random_state=0)
x_train = x_train.T
x_test = x_test.T
y_train = y_train.T
y_test = y_test.T
x_train_poly = x_train.flatten()
x_test_poly = x_test.flatten()

phi_X_poly1 = Polynomial(x_train_poly, 1)
phi_X_poly2 = Polynomial(x_train_poly, 2)
phi_X_poly3 = Polynomial(x_train_poly, 3)
phi_X_gauss = Gaussian(x_train)[0]
phi_X_sigm = Sigmoid(x_train)[0]

DM_poly1 = phi_X_poly1
DM_poly2 = phi_X_poly2
DM_poly3 = phi_X_poly3
DM_gauss = DesignMatrix(phi_X_gauss)
DM_sigm = DesignMatrix(phi_X_sigm)

w_opt_poly1 = OptimalWeight(DM_poly1, y_train)
w_opt_poly2 = OptimalWeight(DM_poly2, y_train)
w_opt_poly3 = OptimalWeight(DM_poly3, y_train)
w_opt_gauss = OptimalWeight(DM_gauss, y_train)
w_opt_sigm = OptimalWeight(DM_sigm, y_train)

phi_X_poly1_test = Polynomial(x_test_poly, 1)
phi_X_poly2_test = Polynomial(x_test_poly, 2)
phi_X_poly3_test = Polynomial(x_test_poly, 3)
phi_X_gauss_test = Gaussian(x_test)[0]
phi_X_sigm_test = Sigmoid(x_test)[0]

DM_poly1_test = phi_X_poly1_test
DM_poly2_test = phi_X_poly2_test
DM_poly3_test = phi_X_poly3_test
DM_gauss_test = DesignMatrix(phi_X_gauss_test)
DM_sigm_test = DesignMatrix(phi_X_sigm_test)

N_test = DM_poly1_test.shape[0]
y_poly1_test= np.array([Model(w_opt_poly1, DM_poly1_test[n,:]) for n in range(N_test)])
y_poly2_test= np.array([Model(w_opt_poly2, DM_poly2_test[n,:]) for n in range(N_test)])
y_poly3_test= np.array([Model(w_opt_poly3, DM_poly3_test[n,:]) for n in range(N_test)])
y_gauss_test = np.array([Model(w_opt_gauss, DM_gauss_test[n,:]) for n in range(N_test)])
y_sigm_test = np.array([Model(w_opt_sigm, DM_sigm_test[n,:]) for n in range(N_test)])

mse_poly1 = mean_squared_error(y_poly1_test, y_test)
mse_poly2 = mean_squared_error(y_poly2_test, y_test)
mse_poly3 = mean_squared_error(y_poly3_test, y_test)
mse_gauss = mean_squared_error(y_gauss_test, y_test)
mse_sigm = mean_squared_error(y_sigm_test, y_test)

R2_poly1 = r2_score(y_poly1_test, y_test)
R2_poly2 = r2_score(y_poly2_test, y_test)
R2_poly3 = r2_score(y_poly3_test, y_test)
R2_gauss = r2_score(y_gauss_test, y_test)
R2_sigm = r2_score(y_sigm_test, y_test)

print('MSE_poly1 = ', mse_poly1)
print('MSE_poly2 = ', mse_poly2)
print('MSE_poly3 = ', mse_poly3)
print('MSE_gauss = ', mse_gauss)
print('MSE_sigm = ', mse_sigm)

print('R2_poly1 = ', R2_poly1)
print('R2_poly2 = ', R2_poly2)
print('R2_poly3 = ', R2_poly3)
print('R2_gauss = ', R2_gauss)
print('R2_sigm = ', R2_sigm)

from sklearn import linear_model

clf = linear_model.LinearRegression()
clf.fit(x_train.T, y_train.T)
pred = clf.predict(x_test.T)
mse = mean_squared_error(y_test.flatten(), pred)
R2 = clf.score(x_test.T, y_test.T)

print('mse = ', mse)
print('R^2 = ', R2)

xlist = np.arange(np.min(x_train), np.max(x_train), 0.01)
Xlist = np.array([xlist])
ylist_poly1 = [Model(w_opt_poly1, Polynomial(x, 1)) for x in xlist]
ylist_poly2 = [Model(w_opt_poly2, Polynomial(x, 2)) for x in xlist]
ylist_poly3 = [Model(w_opt_poly3, Polynomial(x, 3)) for x in xlist]

DM_gauss_graph = DesignMatrix(Gaussian(Xlist)[0])
DM_sigm_graph = DesignMatrix(Sigmoid(Xlist)[0])

N_graph = DM_gauss_graph.shape[0]
ylist_gauss = np.array([Model(w_opt_gauss, DM_gauss_graph[n,:]) for n in range(N_graph)])
ylist_sigm = np.array([Model(w_opt_sigm, DM_sigm_graph[n,:]) for n in range(N_graph)])

plt.plot(xlist, ylist_poly1)
plt.plot(x_train_poly, y_train, 'o')
plt.show()

plt.plot(xlist, ylist_poly2)
plt.plot(x_train_poly, y_train, 'o')
plt.show()

plt.plot(xlist, ylist_poly3)
plt.plot(x_train_poly, y_train, 'o')
plt.show()

plt.plot(xlist, ylist_gauss)
plt.plot(x_train_poly, y_train, 'o')
plt.show()

plt.plot(xlist, ylist_sigm)
plt.plot(x_train_poly, y_train, 'o')
plt.show()

plt.plot(xlist, clf.predict(np.array([xlist]).T))
plt.plot(x_train_poly, y_train, 'o')
plt.show()

python