【超初心者向け】複素NMFとは？更新式を丁寧に導出。

この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多少意訳した部分もあります。ですので，参考程度におさめていただければ幸いです。間違えている箇所がございましたらご指摘ください。随時更新予定です。

実装

こちらのURLよりGitHubのページにアクセスしてください。

単純なNMFについて

複素NMF（非負値行列因子分解）は、通常のNMFにおけるモデル化の弱点を補う形で考案された手法です。通常のNMFについては、以下の記事をご覧ください。

【超初心者向け】NMFとは？更新式を丁寧に導出。この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多...

【超初心者向け】NMF（非負値行列因子分解）と最尤推定この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多...

複素NMFとは？

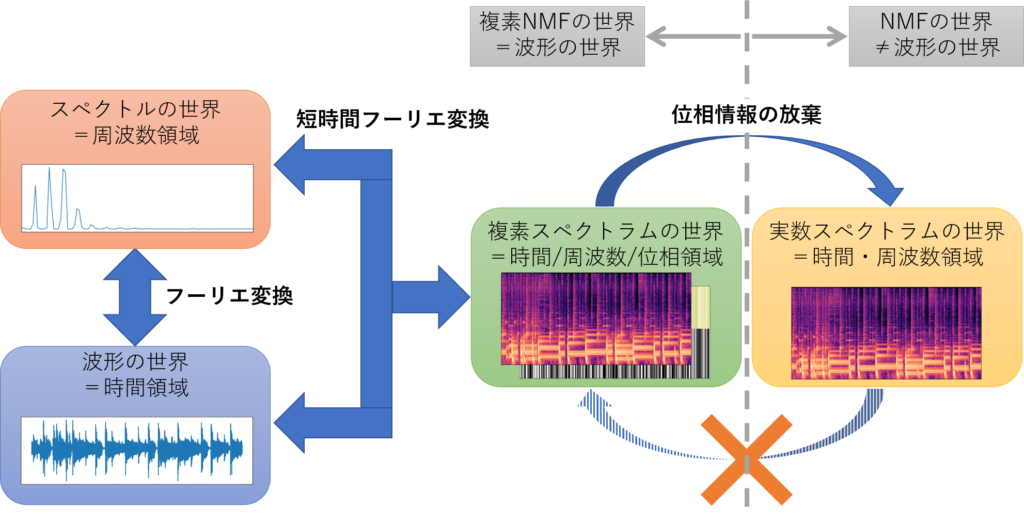複素NMFの概念図

音源分離において、従来のNMFは混合音のスペクトルを、音源の種類とみなせる基底行列と各音源のアクティベーションとみなせるスパースな係数行列に分解できるという面で優れた手法でした。しかし、NMFという手法の構造上、以下の仮定を前提としていました。

これらの仮定は、実際には成り立ちません。なぜならば、まず第一に複素スペクトルから振幅・パワースペクトルへの変換は非線形であり、加法性が成り立たないからです。また、各構成音（例えば「ピアノのド」という音）の周波数成分の振幅比は時変です。ピアノの構成音の周波数が「常に同じ振幅比を保つ」というのは、傾向としてはそう捉えられますが厳密には成り立たない仮定です。

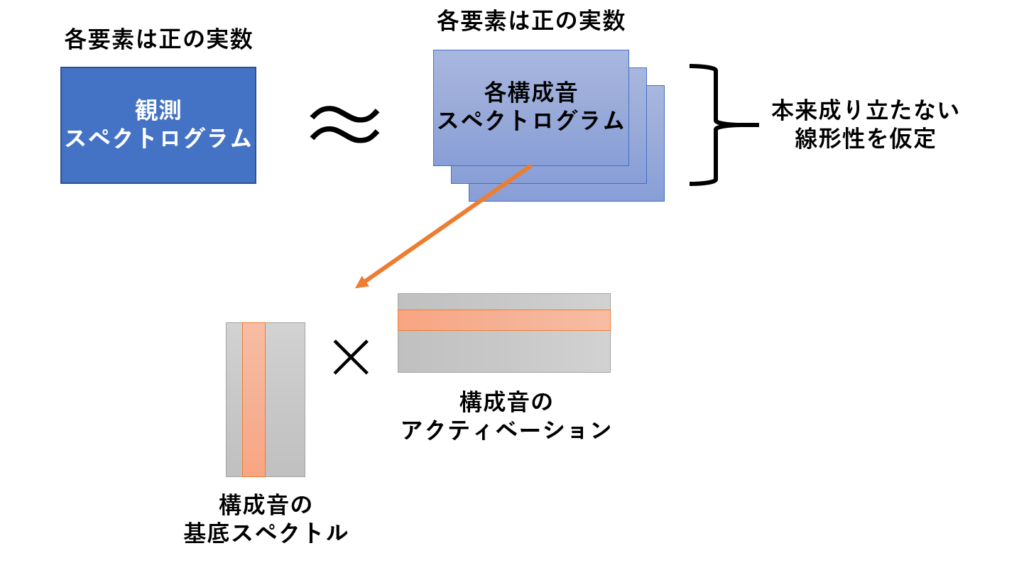NMFが仮定する加法性

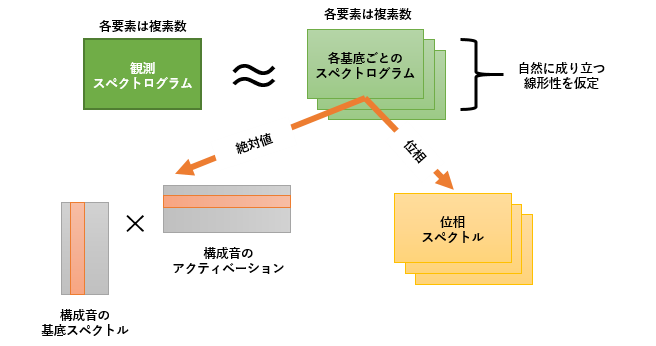複素NMFが仮定する加法性

NMFと似たスパース信号表現として、時間領域信号基底の線形結合により任意の信号を表すSC（スパースコーディング）が挙げられます。SCでは、NMFとは異なりスパース性コストを表すペナルティを導入することで強制的に表現をスパース化します。しかし、分解された信号には冗長性が含まれています。つまり、波形の微妙な差異によって異なる基底と判断されてしまうのが欠点です。

つまり、NMFにはモデル自体に欠陥があると考えられます。SCについても、妥当なモデルではないと考えられます。そこで、NMFの利点である「スパースな信号分解」をベースにして、新しい手法として考案されたのが複素NMFになります。

複素NMFは加法性が成り立つ複素スペクトグラム領域でモデルを考えます。ただし、複素NMFには３階のテンソルが含まれるため、NMFやSCなどと同じように行列表現でモデルを表記できません。そのため、根本的に異なるモデル化だといえます。しかし、３階テンソルが２階テンソルとして捉えられるとき（時不変の制約を付けると）複素NMFはSCと本質的に一致します。

実際に、複素NMFを用いることで、従来のNMFを用いたモノラルチャネル音源分離の性能が上がることが示されています。

それでは、以下で数式を用いて複素NMFによるスパース信号分解表現を見ていきましょう。

複素NMFモデルの定式化

NMFのモデルに、時変の位相スペクトルをパラメータとして付加したものが複素NMFの定式化になります。

\begin{eqnarray}
Y_{k,m} \simeq F_{k,m} = \sum_{l} H_{k,l}U_{l,m}e^{j\phi_{k,l,m}}
\end{eqnarray}

\begin{eqnarray}
&Y_{k,m}& \in \mathbb{ C }\\
&F_{k,m}& \in \mathbb{ C }\\
&H_{k,l}& \in \mathbb{ R }^{K \times L}_{+}\\
&U_{l,m}& \in \mathbb{ R }^{L \times M}_{+}\\
&e^{j\phi_{k,l,m}}& \in \mathbb{ C }
\end{eqnarray}

となっています。更新式は、NMF同様$Y_{k,m}$と$F_{k,m}$の乖離度を目的関数とした補助関数法を用いて導出します。乖離度の指標は、ユークリッド距離もしくはIダイバージェンスが用いられます。ただし、NMFとは異なりモデルが本質的にSCと同じであるとみなせるため、スパース化制約項を付けなくてはいけません。

以上の流れをまとめます。

さて、以下では式（7）の補助関数を見つけていきましょう。補助関数法については、以下の記事をご覧ください。

【超初心者向け】NMFとは？更新式を丁寧に導出。この記事では，研究のサーベイをまとめていきたいと思います。ただし，全ての論文が網羅されている訳ではありません。また，分かりやすいように多...

補助関数の導出

まず、式（7）の第一項目について考えていきましょう。二次関数は凸関数ですので、Jensenの不等式が利用できます。

以下では、Jensenの不等式を利用するために

\begin{eqnarray}
&&\sum_{l} X_{k,l,m} = Y_{k,m}\\
&&0 \leq \beta_{k,l,m} \leq 1\\
&&\sum_{l} \beta_{k,l,m} = 1
\end{eqnarray}
となる$X_{k,l,m}, \beta_{k,l,m}$を導入します。これらを用いて、第一項目にJensenの不等式を利用します。

等号は

のときに成り立ちます。続いて、第二項目について考えていきます。$p$次関数という扱いが難しい関数のため、Jensenの不等式を利用するという方針ではなく、「補助関数の要件を満たすような不等式を作る」という方針でいきます。ここは複素NMFの導出の中で、最も巧妙かつ天下り的な箇所なので、あまり深く考えすぎないようにしてください。

具体的には、$0 \lt p \leq 2$という条件をうまく用います。そのためには、新しい補助変数を導入する必要があります。（１つの不等式につき１つの補助変数が必要）

\begin{eqnarray}
V_{l,m} \geq 0
\end{eqnarray}

となるような$V_{l,m}$を用いて、$V_{l,m} = U_{l,m}$のときに最小値$U_{l,m}^p$を取るような関数を作ることができれば補助関数の要件を満たします。

そこで、導関数が$U_{l,m} = V_{l,m}$のときにのみ0になり（厳密には$U_{l,m} = 0$でも0になる）、最小値0を取るような$U_{l,m}$の関数を作ることができれば、その関数から不等式を作ることができます。実際に作ってみます。

$0 \lt p \leq 2$に注意すると、$U_{k,m}$の関数$f$は$U_{k,m} = V_{k,m}$のときに最小値0を取ります。この関数を用いると、不等式が完成します。

ただし、等号成立条件は$U_{k,m} = V_{k,m}$です。

以上、２種類の不等式を用いると、補助関数$\mathcal{G}_{EU}$が完成します。

たしかに

であり

のとき等号が成立するので、補助関数の要件を満たします。

更新式の導出

以下では、複素NMFの更新式を導出したいと思います。補助関数法の考え方から、まずは補助関数を最小化する補助変数を求めます。次に、最小化された補助関数を最小化する初期パラメータを求めます。それでは、順にやっていきましょう。

不等式の導出の過程から、補助関数を最小化する補助変数は式（33）式（34）で与えられます。次に、補助関数を$\boldsymbol{H},\boldsymbol{U},\boldsymbol{\phi}$についてそれぞれ偏微分して更新式を求めていきます。

ただし、分解のスケールの任意性を除くため

\begin{eqnarray}
\sum_{l} H_{k,l} = 1
\end{eqnarray}

と$l$に関して和が1になるように$H_{k,l}$に制約を付けることにします。

しかし、以下では簡単のために補助関数を最小化する$H_{k,l}$を求めてから、式（35）を満たすように正規化することにします。まず、補助関数で$H_{k,l}$に関する項のみ取り出します。

ただし、$X^\ast$は$X$の共役複素数を表します。この補助関数を$H_{k,l}$に関して偏微分します。

実際に、式（41）を満たす$H_{k,l}$は補助関数を最小化します。なぜならば、$\frac{ \partial^2 \mathcal{G}_{EU} }{ \partial H^2_{k,l} } \geq 0$だからです。これを$H_{k,l}$に関して整理しましょう。

\begin{eqnarray}
H_{k,l} =
\frac{\sum_{m} \frac{U_{l,m}Re[X^\ast_{k,l,m}e^{j\phi_{k,l,m}}]}{\beta_{k,l,m}}}{\sum_{m} \frac{U^2_{l,m}}{\beta_{k,l,m}}}
\end{eqnarray}

見事、更新式が導出されました。ただし、$Re[X]$は$X$の実部を表します。また、上でお伝えしたように、実装の際には$H_{k,l}$に関して正規化が必要なことも覚えておきましょう。

同じようにして、$U_{k,l,m}$の更新式も求めましょう。$H_{k,l}$とは違って、偏微分するときにスパース制約化項まで含めなくてはいけないことに注意しましょう。

この補助関数を$U_{l,m}$に関して偏微分します。

実際に、式（48）を満たす$U_{l,m}$は補助関数を最小化します。なぜならば、$\frac{ \partial^2 \mathcal{G}_{EU} }{ \partial U^2_{l,m} } \geq 0$だからです。これを$U_{l,m}$に関して整理しましょう。

\begin{eqnarray}
U_{l,m} =
\frac{\sum_{k} \frac{H_{k,l}Re[X^\ast_{k,l,m}e^{j\phi_{k,l,m}}]}{\beta_{k,l,m}}}{\sum_{k} \frac{H^2_{k,l}}{\beta_{k,l,m}} + \lambda pV^{p-2}_{k,l,m}}
\end{eqnarray}

見事、更新式が導出されました。残る更新式は、$\phi$に関してです。まずは、目的関数の中で$\phi$に関する項だけ取り出しましょう。

\begin{eqnarray}
|A| &=& \frac{X_{k,l,m}H_{k,l}U_{l,m}}{\beta_{k,l,m}}\\
\cos a_{k,l,m} &=& \frac{Re[X]}{|X|}\\
\sin a_{k,l,m} &=& \frac{Im[X]}{|X|}
\end{eqnarray}

となります。ただし、$Im[X]$は$X$の虚部を表します。さて、私たちの目的は式（53）を最小化する$\phi$を求めることでした。今回は、今までのように偏微分する必要はなく、$\cos(\phi – a_{k,l,m})$が最小になる$\phi$を求めるだけです。

したがって、$\phi$の更新式は以下のようになります。

\begin{eqnarray}
e^{\phi_{k,l,m}}
&=& \cos\phi + j\sin\phi \\
&=& \cos a_{k,l,m} + j\sin a_{k,l,m}\\
&=& \frac{Re[X]}{|X|} + j\frac{Im[X]}{|X|}\\
&=& \frac{X}{|X|}
\end{eqnarray}

となります。さて、全てのモデルパラメータの更新式が出そろいましたが、効率の良い順番でモデルパラメータを更新していきましょう。具体的には、補助変数の更新の後に、$\phi$を更新してしまってから、$H$と$U$を更新するようにします。ですので、$\phi$の更新式を$H$と$U$の更新式に代入します。

\begin{eqnarray}
H_{k,l}
&=& \frac{\sum_{m} \frac{U_{l,m}Re[\frac{|X|^2}{|X|}]}{\beta_{k,l,m}}}{\sum_{m} \frac{U^2_{l,m}}{\beta_{k,l,m}}}\\
&=& \frac{\sum_{m} \frac{U_{l,m}|X|}{\beta_{k,l,m}}}{\sum_{m} \frac{U^2_{l,m}}{\beta_{k,l,m}}}\\
\end{eqnarray}

\begin{eqnarray}
U_{l,m}
&=& \frac{\sum_{k} \frac{H_{k,l}Re[\frac{|X|^2}{|X|}]}{\beta_{k,l,m}}}{\sum_{k} \frac{H^2_{k,l}}{\beta_{k,l,m}} + \lambda pV^{p-2}_{k,l,m}}\\
&=& \frac{\sum_{k} \frac{H_{k,l}|X|}{\beta_{k,l,m}}}{\sum_{k} \frac{H^2_{k,l}}{\beta_{k,l,m}} + \lambda pV^{p-2}_{k,l,m}}
\end{eqnarray}

以上で、複素NMFの更新式の導出は終了です。以下にアルゴリズムをまとめておきます。

複素NMFの発展

●KLダイバージェンス基準の複素NMF
●位相制約付き複素NMF
●無矛盾制約付き複素NMF

などが挙げられます。詳しくは，以下の論文を参考にしてください。

ABOUT ME

zuka

京都大学で機械学習を学んでいます。

BLOG：https://academ-aid.com/